BZOJ-3040-最短路(road)

Description

N个点，M条边的有向图，求点1到点N的最短路（保证存在）。
1<=N<=1000000，1<=M<=10000000

Input

第一行两个整数N、M，表示点数和边数。
第二行六个整数T、rxa、rxc、rya、ryc、rp。

前T条边采用如下方式生成：
1.初始化x=y=z=0。
2.重复以下过程T次：
x=(x*rxa+rxc)%rp;
y=(y*rya+ryc)%rp;
a=min(x%n+1,y%n+1);
b=max(y%n+1,y%n+1);
则有一条从a到b的，长度为1e8-100*a的有向边。

后M-T条边采用读入方式：
接下来M-T行每行三个整数x,y,z，表示一条从x到y长度为z的有向边。

1<=x,y<=N，0<z,rxa,rxc,rya,ryc,rp<2^31

Output

一个整数，表示1~N的最短路。

Sample Input

3 3
0 1 2 3 5 7
1 2 1
1 3 3
2 3 1

Sample Output

2

HINT

【注释】

请采用高效的堆来优化Dijkstra算法。

Source

WC2013营员交流-lydrainbowcat

 

题解

这道题正解要用配对堆

但其实stl的普通堆也可以卡过，重点是卡过

自己不知道RE和TLE了多久

AC代码: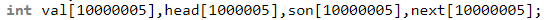

RE代码:

这样我还能说什么0.0

 #include<queue>
 #include<cstdio>
 #include<algorithm>
 #define ll long long
 #define zcr pair<int,int>
 using namespace std;
 int tot;
 int next[],head[],son[],val[];
 ll dis[];
 bool vis[];
 int read(){
     int tmp=; char ch=getchar();
     while (ch<''||ch>'') ch=getchar();
     while (ch>=''&&ch<='') tmp=tmp*+ch-'',ch=getchar();
     return tmp;
 }
 void add(int x,int y,int z){
     next[++tot]=head[x];
     head[x]=tot;
     son[tot]=y;
     val[tot]=z;
 }
 priority_queue<zcr,vector<zcr>,greater<zcr> > q;
 int main(){
     int n,m;
     n=read(),m=read();
     int T,rxa,rxc,rya,ryc,rp;
     T=read(),rxa=read(),rxc=read(),rya=read(),ryc=read(),rp=read();
     int a,b,x,y;
     for (int i=;i<=T;i++){
         x=(x*rxa+rxc)%rp;
         y=(y*rya+ryc)%rp;
         a=min(x%n+,y%n+);
         b=max(y%n+,y%n+);
         add(a,b,-*a);
     }
     for (int i=;i<=m-T;i++){
         int u=read(),v=read(),s=read();
         add(u,v,s);
     }
     for (int i=;i<=n;i++) dis[i]=1ll<<;
     dis[]=;
     q.push(make_pair(,));
     while (!q.empty()){
         int x=q.top().second;
         q.pop();
         if (vis[x]) continue;
         vis[x]=true;
         for (int i=head[x];i;i=next[i]){
             int v=son[i];
             if (dis[v]>dis[x]+val[i]){
                 dis[v]=dis[x]+val[i];
                 q.push(make_pair(dis[v],v));
             }
         }
     }
     printf("%d\n",dis[n]);
     return ;
 }