Canvas 实现灵动的红鲤鱼动画(上)
前言
上一篇文章《Canvas 仿百度贴吧客户端 loading 小球》实现了百度贴吧客户端的 loading 小球效果,同时还留下了一个任务:实现灵动的红鲤鱼动画。
这个动画效果实现起来比较难,需要良好的数学基础。而中学时学到的三角函数知识,早就还给数学老师了。现在一边练习一边写这篇文章,并不能保证最后能实现这个动画效果。
实现过程
第零步:绘制重心
画出鲤鱼的重心。为了方便看效果,以重心为原点,绘制了两条简单的坐标轴。

<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>Title</title>
<style>
canvas {
width: 500px;
height: 500px;
border: 1px solid #ccc;
}
</style>
</head>
<body>
<canvas id="canvas" width="500" height="500"></canvas>
<script>
var canvas = document.getElementById('canvas')
canvas.width = 500
canvas.height = 500
var ctx = canvas.getContext('2d')
var width = canvas.width
var height = canvas.height
// 重心 middle point
var mPt = {
x: 250,
y: 250
}
var R = 30 // 鱼头半径
var angle = 0 // 鱼的角度
// x 坐标
ctx.fillStyle='#000'
ctx.beginPath()
ctx.moveTo(0, mPt.y)
ctx.lineTo(width, mPt.y)
ctx.stroke()
// y 坐标
ctx.beginPath()
ctx.moveTo(mPt.x, 0)
ctx.lineTo(mPt.x, height)
ctx.closePath()
ctx.stroke()
function drawPt(pt) {
ctx.fillStyle = '#000'
ctx.beginPath()
ctx.arc(pt.x, pt.y, 4, 0, 2 * Math.PI)
ctx.fill()
}
// 重心
drawPt(mPt)
</script>
</body>
</html>第一步:绘制鱼头
首先需要求出鱼头的坐标。
先定义一个函数,能根据一个点的坐标,相对这个点的角度和距离,求出另一个点的坐标。
function getPt(pt, angle, length) {
return {
x: pt.x + length * Math.cos(angle * Math.PI / 180),
y: pt.y - length * Math.sin(angle * Math.PI / 180)
}
}由于鱼头位于鱼前进方向,距离重心 1.5R 的位置,先求出鱼头的位置:
var headPt = getPt(mPt, angle, 1.5 * R) // 鱼头位置
drawPt(headPt)然后以鱼头位置为圆心,半径为 R 的绘制圆形:
// 绘制鱼头
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.arc(headPt.x, headPt.y, R, 0, 2 * Math.PI)
ctx.fill()效果如下:
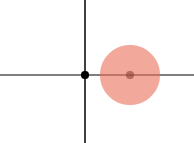
第二步:绘制鱼身
鱼身不是一个规则的图形,它是由两条直线和两条曲线组成的闭合路径。曲线可以用贝塞尔曲线绘制。
我们先绘制鱼左边的身体,首先需要求出左侧贝塞尔曲线的三个控制点:

从图可以看出,当鱼的角度为 0° 时,控制点 bodyLeft1 位于重心右方向 1.5R、上方向 R 的位置。
我写了一个函数,能根据 0° 时点的坐标求出任意度时点的坐标,源码如下。实现原理是,先求出该点距离重心的距离(鱼旋转时,该点距离重心的距离不变)和角度,再根据鱼的方向求出正确的位置。
function quickPt(pt) {
var length = Math.sqrt((pt.x - mPt.x) * (pt.x - mPt.x) + (pt.y - mPt.y) * (pt.y - mPt.y))
var angl = getAngle(mPt, pt)
return getPt(mPt, angle + angl, length)
}
function getAngle(cPt, pt) {
var angl = Math.atan((cPt.y - pt.y) / (pt.x - cPt.x)) * 180 / Math.PI
if (pt.y < cPt.y) {
if (pt.x < cPt.x) {
console.log('第二')
angl = 90 + 90 + angl
}
if (pt.x > cPt.x) {
console.log('第一')
}
} else if (pt.y > cPt.y) {
if (pt.x < cPt.x) {
console.log('第三')
angl = 90 + 90 + angl
}
if (pt.x > cPt.x) {
console.log('第四')
angl = 360 + angl
}
if (pt.x === cPt.x) {
angl = 270
}
} else {
if (pt.x < cPt.x) {
angl = 180
}
}
return angl
}这样的话,三个控制点的位置我们就可以轻易地求出来:
// 身体
var bodyLeft1 = quickPt({x: mPt.x + 1.5 * R, y: mPt.y - R})
drawPt(bodyLeft1)
var bodyLeft2 = quickPt({x: mPt.x, y: mPt.y - 1.5 * R})
drawPt(bodyLeft2)
var bodyLeft3 = quickPt({x: mPt.x - 1.5 * R, y: mPt.y - 0.8 * R})
drawPt(bodyLeft3)效果如下:
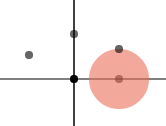
根据三个控制点绘制贝塞尔曲线:
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(bodyLeft1.x, bodyLeft1.y)
ctx.quadraticCurveTo(bodyLeft2.x, bodyLeft2.y, bodyLeft3.x, bodyLeft3.y)
ctx.fill()效果如下:

鱼右边的三个控制点和左边的三个控制点是对称的,再像前面那样求出坐标则显得啰嗦。所以,定义一个函数,能根据某一点的坐标,求出对称点的坐标,两点关于鱼身的中轴线对称。
// 获取对称坐标
function getSymmetricPt(pt) {
var length = Math.sqrt((pt.x - mPt.x) * (pt.x - mPt.x) + (pt.y - mPt.y) * (pt.y - mPt.y))
var angl = getAngle(mPt, pt)
return getPt(mPt, angle * 2 - angl, length)
}原理是两点关于鱼的中轴线对称的话,这两点到重心的距离相等,并且两点与重心的连线与中轴线夹角相等。
因为 (angle1 + angle2) / 2 = angle,所以 angle2 = angle * 2 - angle1
有了这个函数,我们可以轻易求出鱼身体右侧三个控制点的坐标:
var bodyRight3 = getSymmetricPt(bodyLeft3)
drawPt(bodyRight3)
var bodyRight2 = getSymmetricPt(bodyLeft2)
drawPt(bodyRight2)
var bodyRight1 = getSymmetricPt(bodyLeft1)
drawPt(bodyRight1)再通过三个控制点绘制贝塞尔曲线,最后用直线链接两个贝塞尔曲线,填充路径。
身体部分完整代码如下:
// 身体
var bodyLeft1 = quickPt({x: mPt.x + 1.5 * R, y: mPt.y - R})
drawPt(bodyLeft1)
var bodyLeft2 = quickPt({x: mPt.x, y: mPt.y - 1.5 * R})
drawPt(bodyLeft2)
var bodyLeft3 = quickPt({x: mPt.x - 1.5 * R, y: mPt.y - 0.8 * R})
drawPt(bodyLeft3)
var bodyRight3 = getSymmetricPt(bodyLeft3)
drawPt(bodyRight3)
var bodyRight2 = getSymmetricPt(bodyLeft2)
drawPt(bodyRight2)
var bodyRight1 = getSymmetricPt(bodyLeft1)
drawPt(bodyRight1)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(bodyLeft1.x, bodyLeft1.y)
ctx.quadraticCurveTo(bodyLeft2.x, bodyLeft2.y, bodyLeft3.x, bodyLeft3.y)
ctx.lineTo(bodyRight3.x, bodyRight3.y)
ctx.quadraticCurveTo(bodyRight2.x, bodyRight2.y, bodyRight1.x, bodyRight1.y)
ctx.closePath()
ctx.fill()效果如下:
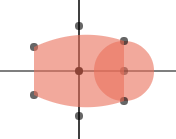
第三步:绘制鱼鳍
// 右鳍
var rightPt1 = getPt(headPt, angle - 110, 0.9 * R)
var rightPt2 = getPt(mPt, angle - 70, 4 * R)
var rightPt3 = getPt(mPt, angle - 90, 0.9 * R)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(rightPt1.x, rightPt1.y)
ctx.quadraticCurveTo(rightPt2.x, rightPt2.y, rightPt3.x, rightPt3.y)
ctx.fill()
// 左鳍
var leftPt1 = getSymmetricPt(rightPt1)
var leftPt2 = getSymmetricPt(rightPt2)
var leftPt3 = getSymmetricPt(rightPt3)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(leftPt1.x, leftPt1.y)
ctx.quadraticCurveTo(leftPt2.x, leftPt2.y, leftPt3.x, leftPt3.y)
ctx.fill()效果:

第四步:绘制鱼尾
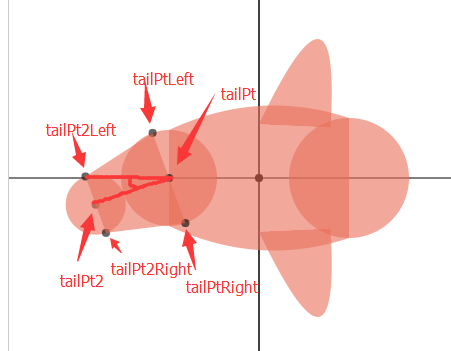
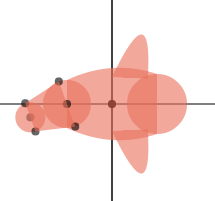
尾部的绘制是一个繁琐而又无味的过程。从上图可以看出,仅仅绘制尾部的前半部分,我们就需要求出 6 个点的坐标。尾部是可以摆动的,所以尾部并不是关于中轴线对称,而是与中轴线有一个偏角,我们定义这个偏角为 tailOffset。上图中,尾部的第一个圆半径为 TAIL_SIZE,即 0.8R;第二个圆半径为 TAIL_SIZE2,即 0.5R。
var TAIL_SIZE = 0.8
var TAIL_SIZE2 = 0.5
var tailOffset = 20
// 尾部
var tailPt = getPt(mPt, 180 + angle, 1.5 * R)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.arc(tailPt.x, tailPt.y, TAIL_SIZE * R, 0, 2 * Math.PI)
ctx.fill()
drawPt(tailPt)
var tailPtLeft = getPt(tailPt, 180 + tailOffset - 90, TAIL_SIZE * R)
drawPt(tailPtLeft)
var tailPtRight = getPt(tailPt, 180 + tailOffset + 90, TAIL_SIZE * R)
drawPt(tailPtRight)
var tailPt2 = getPt(tailPt, 180 + angle + tailOffset, (TAIL_SIZE2 + TAIL_SIZE) * R)
drawPt(tailPt2)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.arc(tailPt2.x, tailPt2.y, TAIL_SIZE2 * R, 0, 2 * Math.PI)
ctx.fill()
var tainPt2Left = getPt(tailPt2, 180 + tailOffset - 90, TAIL_SIZE2 * R)
drawPt(tainPt2Left)
var tailPt2Right = getPt(tailPt2, 180 + tailOffset + 90, TAIL_SIZE2 * R)
drawPt(tailPt2Right)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(tailPtLeft.x, tailPtLeft.y)
ctx.lineTo(tainPt2Left.x, tainPt2Left.y)
ctx.lineTo(tailPt2Right.x, tailPt2Right.y)
ctx.lineTo(tailPtRight.x, tailPtRight.y)
ctx.fill()效果:
继续绘制鱼尾的后半部分,上图:
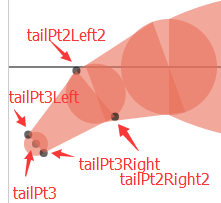
继续无聊的求点连线。。。
var TAIL_SIZE3 = 0.2
var tailPt3 = getPt(tailPt2, 180 + angle + tailOffset + tailOffset2, 1.3 * R)
drawPt(tailPt3)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.arc(tailPt3.x, tailPt3.y, TAIL_SIZE3 * R, 0, 2 * Math.PI)
ctx.fill()
var tainPt2Left2 = getPt(tailPt2, 180 + tailOffset + tailOffset2 - 90, TAIL_SIZE2 * R)
drawPt(tainPt2Left2)
var tailPt2Right2 = getPt(tailPt2, 180 + tailOffset + tailOffset2 + 90, TAIL_SIZE2 * R)
drawPt(tailPt2Right2)
var tainPt3Left = getPt(tailPt3, 180 + tailOffset + tailOffset2 - 90, TAIL_SIZE3 * R)
drawPt(tainPt3Left)
var tailPt3Right = getPt(tailPt3, 180 + tailOffset + tailOffset2 + 90, TAIL_SIZE3 * R)
drawPt(tailPt3Right)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(tainPt2Left2.x, tainPt2Left2.y)
ctx.lineTo(tainPt3Left.x, tainPt3Left.y)
ctx.lineTo(tailPt3Right.x, tailPt3Right.y)
ctx.lineTo(tailPt2Right2.x, tailPt2Right2.y)
ctx.fill()绘制第一个三角形
var triangleCenter = getPt(tailPt2, 180 + angle + tailOffset + tailOffset2, 0.8 * R)
drawPt(triangleCenter)
var triangleLeft = getPt(triangleCenter, 180 + tailOffset + tailOffset2 - 90, 0.6 * R)
drawPt(triangleLeft)
var triangleRight = getPt(triangleCenter, 180 + tailOffset + tailOffset2 + 90, 0.6 * R)
drawPt(triangleRight)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(tailPt2.x, tailPt2.y)
ctx.lineTo(triangleLeft.x, triangleLeft.y)
ctx.lineTo(triangleRight.x, triangleRight.y)
ctx.fill()效果:
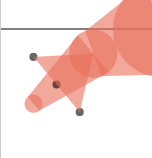
绘制第二个三角形:
var triangle2Center = getPt(tailPt2, 180 + angle + tailOffset + tailOffset2, 1 * R)
drawPt(triangle2Center)
var triangle2Left = getPt(triangle2Center, 180 + tailOffset + tailOffset2 - 90, 0.8 * R)
drawPt(triangle2Left)
var triangle2Right = getPt(triangle2Center, 180 + tailOffset + tailOffset2 + 90, 0.8 * R)
drawPt(triangle2Right)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(tailPt2.x, tailPt2.y)
ctx.lineTo(triangle2Left.x, triangle2Left.y)
ctx.lineTo(triangle2Right.x, triangle2Right.y)
ctx.fill()效果:
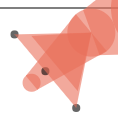
第五步:删除多余的点和线
删除所有 drawPt 代码和坐标轴,就大功告成了!
效果:

总结
虽然最后绘制出了鲤鱼,但这条死气沉沉的鲤鱼显然不够灵动。下一篇,会在模仿的基础上加点小创新,实现更加灵动的小鲤鱼。
参考
附录
附上完整代码:
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>Title</title>
<style>
canvas {
width: 500px;
height: 500px;
border: 1px solid #ccc;
}
</style>
</head>
<body>
<canvas id="canvas" width="500" height="500"></canvas>
<script>
var canvas = document.getElementById('canvas')
canvas.width = 500
canvas.height = 500
var ctx = canvas.getContext('2d')
var width = canvas.width
var height = canvas.height
// 重心 middle point
var mPt = {
x: 250,
y: 250
}
var R = 30 // 鱼头半径
var angle = 0 // 鱼的角度
function drawPt(pt) {
ctx.fillStyle = '#000'
ctx.beginPath()
ctx.arc(pt.x, pt.y, 4, 0, 2 * Math.PI)
ctx.fill()
}
function getPt(pt, angle, length) {
return {
x: pt.x + length * Math.cos(angle * Math.PI / 180),
y: pt.y - length * Math.sin(angle * Math.PI / 180)
}
}
function quickPt(pt) {
var length = Math.sqrt((pt.x - mPt.x) * (pt.x - mPt.x) + (pt.y - mPt.y) * (pt.y - mPt.y))
var angl = getAngle(mPt, pt)
return getPt(mPt, angle + angl, length)
}
function getAngle(cPt, pt) {
var angl = Math.atan((cPt.y - pt.y) / (pt.x - cPt.x)) * 180 / Math.PI
if (pt.y < cPt.y) {
if (pt.x < cPt.x) {
//console.log('第二')
angl = 90 + 90 + angl
}
if (pt.x > cPt.x) {
//console.log('第一')
}
} else if (pt.y > cPt.y) {
if (pt.x < cPt.x) {
//console.log('第三')
angl = 90 + 90 + angl
}
if (pt.x > cPt.x) {
//console.log('第四')
angl = 360 + angl
}
if (pt.x === cPt.x) {
angl = 270
}
} else {
if (pt.x < cPt.x) {
angl = 180
}
}
return angl
}
// 获取对称坐标
function getSymmetricPt(pt) {
var length = Math.sqrt((pt.x - mPt.x) * (pt.x - mPt.x) + (pt.y - mPt.y) * (pt.y - mPt.y))
var angl = getAngle(mPt, pt)
return getPt(mPt, angle * 2 - angl, length)
}
ctx.globalAlpha = '0.6'
var headPt = getPt(mPt, angle, 1.5 * R) // 鱼头位置
// 绘制鱼头
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.arc(headPt.x, headPt.y, R, 0, 2 * Math.PI)
ctx.fill()
// 身体
var bodyLeft1 = quickPt({x: mPt.x + 1.5 * R, y: mPt.y - R})
var bodyLeft2 = quickPt({x: mPt.x, y: mPt.y - 1.5 * R})
var bodyLeft3 = quickPt({x: mPt.x - 1.5 * R, y: mPt.y - 0.8 * R})
var bodyRight3 = getSymmetricPt(bodyLeft3)
var bodyRight2 = getSymmetricPt(bodyLeft2)
var bodyRight1 = getSymmetricPt(bodyLeft1)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(bodyLeft1.x, bodyLeft1.y)
ctx.quadraticCurveTo(bodyLeft2.x, bodyLeft2.y, bodyLeft3.x, bodyLeft3.y)
ctx.lineTo(bodyRight3.x, bodyRight3.y)
ctx.quadraticCurveTo(bodyRight2.x, bodyRight2.y, bodyRight1.x, bodyRight1.y)
ctx.closePath()
ctx.fill()
// 右鳍
var rightPt1 = getPt(headPt, angle - 110, 0.9 * R)
var rightPt2 = getPt(mPt, angle - 70, 4 * R)
var rightPt3 = getPt(mPt, angle - 90, 0.9 * R)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(rightPt1.x, rightPt1.y)
ctx.quadraticCurveTo(rightPt2.x, rightPt2.y, rightPt3.x, rightPt3.y)
ctx.fill()
// 左鳍
var leftPt1 = getSymmetricPt(rightPt1)
var leftPt2 = getSymmetricPt(rightPt2)
var leftPt3 = getSymmetricPt(rightPt3)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(leftPt1.x, leftPt1.y)
ctx.quadraticCurveTo(leftPt2.x, leftPt2.y, leftPt3.x, leftPt3.y)
ctx.fill()
var TAIL_SIZE = 0.8
var TAIL_SIZE2 = 0.4
var TAIL_SIZE3 = 0.15
var tailOffset = 20
var tailOffset2 = 20
// 尾部
var tailPt = getPt(mPt, 180 + angle, 1.5 * R)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.arc(tailPt.x, tailPt.y, TAIL_SIZE * R, 0, 2 * Math.PI)
ctx.fill()
var tailPtLeft = getPt(tailPt, 180 + tailOffset - 90, TAIL_SIZE * R)
var tailPtRight = getPt(tailPt, 180 + tailOffset + 90, TAIL_SIZE * R)
var tailPt2 = getPt(tailPt, 180 + angle + tailOffset, (TAIL_SIZE2 + TAIL_SIZE) * R)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.arc(tailPt2.x, tailPt2.y, TAIL_SIZE2 * R, 0, 2 * Math.PI)
ctx.fill()
var tainPt2Left = getPt(tailPt2, 180 + tailOffset - 90, TAIL_SIZE2 * R)
var tailPt2Right = getPt(tailPt2, 180 + tailOffset + 90, TAIL_SIZE2 * R)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(tailPtLeft.x, tailPtLeft.y)
ctx.lineTo(tainPt2Left.x, tainPt2Left.y)
ctx.lineTo(tailPt2Right.x, tailPt2Right.y)
ctx.lineTo(tailPtRight.x, tailPtRight.y)
ctx.fill()
var tailPt3 = getPt(tailPt2, 180 + angle + tailOffset + tailOffset2, 1.3 * R)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.arc(tailPt3.x, tailPt3.y, TAIL_SIZE3 * R, 0, 2 * Math.PI)
ctx.fill()
var tainPt2Left2 = getPt(tailPt2, 180 + tailOffset + tailOffset2 - 90, TAIL_SIZE2 * R)
var tailPt2Right2 = getPt(tailPt2, 180 + tailOffset + tailOffset2 + 90, TAIL_SIZE2 * R)
var tainPt3Left = getPt(tailPt3, 180 + tailOffset + tailOffset2 - 90, TAIL_SIZE3 * R)
var tailPt3Right = getPt(tailPt3, 180 + tailOffset + tailOffset2 + 90, TAIL_SIZE3 * R)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(tainPt2Left2.x, tainPt2Left2.y)
ctx.lineTo(tainPt3Left.x, tainPt3Left.y)
ctx.lineTo(tailPt3Right.x, tailPt3Right.y)
ctx.lineTo(tailPt2Right2.x, tailPt2Right2.y)
ctx.fill()
var triangleCenter = getPt(tailPt2, 180 + angle + tailOffset + tailOffset2, 0.8 * R)
var triangleLeft = getPt(triangleCenter, 180 + tailOffset + tailOffset2 - 90, 0.6 * R)
var triangleRight = getPt(triangleCenter, 180 + tailOffset + tailOffset2 + 90, 0.6 * R)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(tailPt2.x, tailPt2.y)
ctx.lineTo(triangleLeft.x, triangleLeft.y)
ctx.lineTo(triangleRight.x, triangleRight.y)
ctx.fill()
var triangle2Center = getPt(tailPt2, 180 + angle + tailOffset + tailOffset2, 1 * R)
var triangle2Left = getPt(triangle2Center, 180 + tailOffset + tailOffset2 - 90, 0.8 * R)
var triangle2Right = getPt(triangle2Center, 180 + tailOffset + tailOffset2 + 90, 0.8 * R)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(tailPt2.x, tailPt2.y)
ctx.lineTo(triangle2Left.x, triangle2Left.y)
ctx.lineTo(triangle2Right.x, triangle2Right.y)
ctx.fill()
</script>
</body>
</html>Canvas 实现灵动的红鲤鱼动画(上)的更多相关文章
- [转]自定义Drawable实现灵动的红鲤鱼动画(上篇)
此篇中的小鱼动画是模仿国外一个大牛做的flash动画,第一眼就爱上它了,简约灵动又不失美学,于是抽空试着尝试了一下,如下是我用Android实现的效果图: 小鱼儿 由于整个绘制分析过程比较繁琐所以 ...
- [转]自定义Drawable实现灵动的红鲤鱼动画(下篇)
小鱼儿 上篇文章自定义Drawable实现灵动的红鲤鱼动画(上篇)我们绘制了可以摆动身体的小鱼,本篇就分享一下如何让小鱼游到手指点击的位置.用到的主要技术如下: 1).三阶贝塞尔曲线 2).Pat ...
- 基于canvas与原生JS的H5动画引擎
前一段时间项目组里有一些H5动画的需求,由于没有专业的前端人员,便交由我这个做后台的研究相关的H5动画技术. 通过初步调研,H5动画的实现大概有以下几种方式: 1.基于css实现 这种方式比较简单易学 ...
- P4773 红鲤鱼与绿鲤鱼
P4773 红鲤鱼与绿鲤鱼 暑假比赛的一个水题 总情况数:\(\dfrac{(a+b)!}{a!b!}\) 就是\(a+b\)条鲤鱼中选\(a\) or \(b\)的情况 反正我们会用完鲤鱼,则红鲤鱼 ...
- 基于canvas实现物理运动效果与动画效果(一)
一.为什么要写这篇文章 某年某月某时某种原因,我在慕课网上看到了一个大神实现了关于小球的抛物线运动的代码,心中很是欣喜,故而写这篇文章来向这位大神致敬,同时也为了弥补自己在运动效果和动画效果制作方面的 ...
- HTML5 Canvas 超炫酷烟花绽放动画教程
这是一个很酷的HTML5 Canvas动画,它将模拟的是我们现实生活中烟花绽放的动画特效,效果非常逼真,但是毕竟是电脑模拟,带女朋友看就算了,效果还是差了点,呵呵.这个HTML5 Canvas动画有一 ...
- uniapp中用canvas实现小球碰撞的小动画
uniapp 我就不想喷了,踩了很多坑,把代码贡献出来让大家少踩些坑. 实现的功能: 生成n个球在canvas中运动,相互碰撞后会反弹,反弹后的速度计算我研究过了,可以参考代码直接用 防止球出边框 防 ...
- pygame-KidsCanCode系列jumpy-part10-角色动画(上)
上一节学习如何利用spritesheet加载图片,但是player仍然是一张静态的图片,比较枯燥,我们要让它动起来! Player类,先把各种状态的图片加载起来: # 加载各种状态的图片序列 def ...
- Delphi XE2 之 FireMonkey 入门(12) - 动画(上)
在 HD 窗体上添加一个 TAniIndicator, 修改其 Enabled 属性为 True, 动画完成了. 这是最简单的动画相关的控件了, 只有两个值得注意的属性: Enabled: Boole ...
随机推荐
- Linux命令 比较文件
cmp [功能说明] 比较文件 #cmp可以比较任何类型的文件,并在标准输出设备上显示文件的第一次不同处的行号和字节号,分别从1开始,但是一般用于比较文本文件 [语法格式] Cmp[参数][文件1][ ...
- 自动清理SQLServerErrorLog错误日志避免太大
问题描述:开启SQLServer自动备份后,备份文件越来越多,有没有及时清理,导致服务器空间不足,备份出错,以至于出现几个G的ErrorLog文件,影响系统的登录管理. 解决办法:定期清理SQLSer ...
- sqlserver isnull判断
--在新增或编辑的时候设置默认值或加isnull判断 Sql isnull函数 ISNULL(columName, 0)<>35 或 ISNULL(columName, '')<&g ...
- 《JavaScript高级程序设计》笔记一
第一章 JavaScript简介 一.JavaScript的起源 JavaScript诞生于1995年.当时,它的主要作用是处理一些输入验证操作.之前的话,都是把表单数据发送到服务器端,然后再去判断有 ...
- vmware提示:此虚拟机似乎正在使用中,取得该虚拟机的所有权失败错误
用vm的时候,没有挂起和关闭虚拟机,直接关实体机.然后不幸的就异常了. 启动提示:此虚拟机似乎正在使用中.如果此虚拟机已在使用中,请按"取消"按钮,以免损坏它.如果此虚拟机未使用, ...
- mysql安装不上 failed to install the service
先前安装的没有卸载干净必须删除相应的注册表方法如下:1)“运行”中敲入“Regedit”进入注册表编辑2)HKEY_LOCAL_MACHINE->SYSTEM->ControlSet001 ...
- AS中layout_gravity与gravity的区别
gravity 这个英文单词是重心的意思,在这里就表示停靠位置的意思. android:layout_gravity 和 android:gravity 的区别 从名字上可以看到,android:gr ...
- 【Android Developers Training】 81. 解析XML数据
注:本文翻译自Google官方的Android Developers Training文档,译者技术一般,由于喜爱安卓而产生了翻译的念头,纯属个人兴趣爱好. 原文链接:http://developer ...
- JavaScript深入浅出补充——(一)数据类型,表达式和运算符
项目基本做完,在进行下一阶段学习之前先看视频学习回顾一下JavaScript 一.数据类型 JavaScript中有五种原始类型和一种对象类型 JavaScript弱类型语言中隐式转换 num-0 字 ...
- Spring MVC 项目搭建 -5- spring security 使用数据库进行验证
Spring MVC 项目搭建 -5- spring security 使用数据库进行验证 1.创建数据表格(这里使用的是mysql) CREATE TABLE security_role ( id ...
