贪心问题：区间覆盖 NYOJ 喷水装置（二）

喷水装置（二）

时间限制：3000 ms  |  内存限制：65535 KB

难度：4

描述

有一块草坪，横向长w,纵向长为h,在它的橫向中心线上不同位置处装有n(n<=10000)个点状的喷水装置，每个喷水装置i喷水的效果是让以它为中心半径为Ri的圆都被润湿。请在给出的喷水装置中选择尽量少的喷水装置，把整个草坪全部润湿。

输入

第一行输入一个正整数N表示共有n次测试数据。
每一组测试数据的第一行有三个整数n,w,h，n表示共有n个喷水装置，w表示草坪的横向长度，h表示草坪的纵向长度。
随后的n行，都有两个整数xi和ri,xi表示第i个喷水装置的的横坐标（最左边为0），ri表示该喷水装置能覆盖的圆的半径。

输出

每组测试数据输出一个正整数，表示共需要多少个喷水装置，每个输出单独占一行。
如果不存在一种能够把整个草坪湿润的方案，请输出0。

样例输入

样例输出

题解：

题目分析：本题可以看作是区间覆盖问题，将每个圆的喷射范围映射到区间内。可转换为：如图，数轴上有n个区间[a-x,a+x]（如图），选择尽量少的区间覆盖[0,w]。

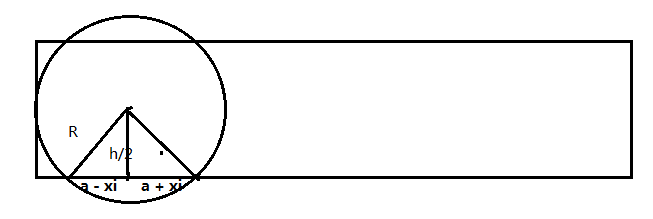
贪心策略

把各区间按照 起点 从小到大排序，从前向后遍历，然后每次选择 从当前位置起点 开始的最长区间，并以这个区间的最右端 为新的起点，继续选择，直到找不到区间 覆盖当前位置起点 或者 当前位置起点 已经到达线段末端。

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <cmath>
using namespace std;

const int maxn =  + ;
double Distance(double ri, double h);
void solve();

struct Water {
    double    left,
            right;
    Water(double lh = , double rh = ) : left(lh), right(rh) {
    }
} wats[maxn];

bool cmp(const Water& a, const Water& b)
{
    return a.left < b.left;
}

double Distance(double ri, double h)
{
    return sqrt(ri * ri - h * h / );
}

void solve()
{
    int N;
    int n, w, h;

    int xi, ri;

    cin >> N;

    while (N--)
    {
        int cnt = ;
        int ans = ;

        cin >> n >> w >> h;

        for (int i = ; i < n; i++)
        {
            cin >> xi >> ri;

            if (ri* < h) continue;
            double dis = Distance(ri, h);
            wats[cnt].left = xi - dis;
            wats[cnt++].right = xi + dis;

        }
        //排序的范围是  cnt !!!!!! 不是 n 了！！阿西吧，好气哦
        sort(wats, wats + cnt, cmp);

        double current_sum = ;
        int flag = ;

        while (current_sum < w)
        {
            double max = ;

//                每次选择从当前起点S开始的最长区间，并以这个区间的右端点为新的起点
            for (int j = ; j < cnt; j++)
            {
                if (wats[j].left <= current_sum && wats[j].right - current_sum > max) {
                    max = wats[j].right - current_sum;     //选择从 current_Sum开始的，最长区间
                }
            }
            if (max)
            {
                ans++;
                current_sum += max;      //当前位置向后移动
            }
            else
            {
                //最后一个区间的末尾 不能 比 current_sum 大 ==> 显然不存在解
                flag = ;
                break;
            }
        }
        if (!flag) {
            cout <<  << endl;
        }
        else {
            cout << ans << endl;
        }
    }
}

int main()
{
    solve();

    return ;
}