【DP】【CF1097D】 Makoto and a Blackboard

更好的阅读体验

Description

给定一个数 $n$，对它进行 $k$ 次操作，每次将当前的数改为自己的因数，包括 $1$ 和自己。写出变成所有因数的概率是相等的。求 $k$ 次以后 $n$ 期望会变成多少

Input

一行两个整数 $n,k$

Output

一行一个整数代表答案

Hint

$1~\leq~n~\leq~10^{15}~,~1~\leq~k~\leq~10^4$

Solution

Hello 2019！

我们考虑整个数字变化的树形图：

以 $n~=~6~,~k~=~2$ 为例：

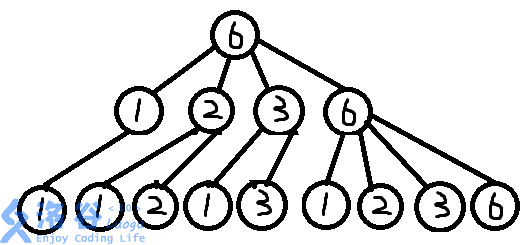
（恕我直言，这图是真的丑）

然后我们将这张图改一下，要求每个非叶节点都有 $4$ 个孩子，如果孩子数不足，就让他们平分这四个。于是新的变化图如下：

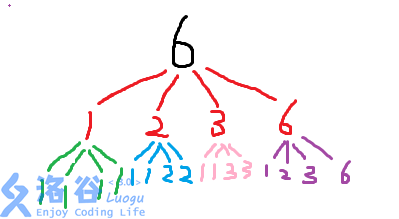
（恕我直言，这图更丑了）

我们发现这张图上所有叶节点出现的概率都是等可能的，并且他们包含了所有的情况，所以求出这些数字的和再除以节点数就是期望值。

接着考虑由于一个数字的所有质因数都是独立的，同时每个质因子都可以画出类似的转移图，依据唯一分解定理，我们可以将质因子拆开，对于每个质因子求出他们期望变成多少，然后乘起来即为总期望。这里的质因子包括了质数 $p$ 和它的指数 $c$。

接着考虑我们对质因子DP。一次对 $p^c$ 的操作相当于将其变成 $p^0,p^1,p^2,\dots p^c$ 中的任意一个。于是我们可以将一次操作转化成将指数 $c$ 变成 $[1,c]$ 中任意一个数。我们规定任何一个节点都有 $d(n)$ 个孩子， $d(n)$ 为 $n$ 的因数个数。则对于一个数值为 $x$ 的节点，她有 $\frac{1}{x + 1}$ 的概率变成 $y~(0~\leq~y~\leq~x)$，那么它会占据 $x$ 的 $\frac{d(n)}{x + 1}$ 个孩子。

例如，对于 $2^2$ 进行 $2$ 次变化的指数图如下

我们认为粉色的位置每个数占据了 $\frac{1}{2}$ 个儿子

于是我们考虑当我们进行了 $i$ 次变化，第 $w$ 个质因子在树形图上的第 $i$ 层指数数值为 $j$ 的节点个数，则显然有

\[f_{w,i,j}~=~\sum_{h = j}^{c_w}~f_{w,i - 1,h}~\times~\frac{d(n)}{h + 1}
\]

其中 $c_j$ 为 $n$ 的唯一分解式中对应项的指数。

于是我们枚举 $n$ 的因数，求出他们出现的次数与他们值的乘积，除以最下面一层的节点个数即为答案

\[\begin{aligned}ans~& =~\frac{1}{d^k(n)}~\sum_{x \mid n}~Times_d~\times~x\\&=\frac{1}{d^k(n)}~\sum_{x \mid n}~d~\prod_{i = 1}^{d(n)}~f_{i,k,h}\end{aligned}
\]

其中 $h$ 为 $d$ 唯一分解式对应项的指数。

我们发现在 DP时，第 $k$ 层每个位置都被乘了 $d^k(n)$，于是可以和式子中的 $\frac{1}{d^k(n)}$ 约掉，式子变为

\[f_{w,i,j}~=~\sum_{h = j}^{c_w}~f_{w,i - 1,h}~\times~\frac{1}{h + 1}
\]

\[\begin{aligned}ans~& =~\sum_{x \mid n}~Times_d~\times~x\\&=~\sum_{x \mid n}~d~\prod_{i = 1}^{d(n)}~f_{i,k,h}\end{aligned}
\]

看起来舒服多了。

考虑复杂度：我们枚举了 $k$ 层，每层枚举了 $n$ 的质因数个数次，这里的质因数不包括指数，但是包括重复的，例如 $p^2$ 算作两个质因数。由于一个数 $n$ 的质因数为 $O(\log n)$，所以总状态复杂度为 $O(k \log n)$。在转移时，我们枚举的上界是 $O(\log n)$，所以总复杂度为 $O(k~\log^2 n)$。发现转移的位置事实上转移了一个加权后缀和，于是我们再开一个数组维护这个后缀和即可做到 $O(k \log n)$。

注意到这样会爆空间，但是发现对于每个DP状态我们只需要第 $k$ 层的情况，并且第一维互不影响，于是我们可以把第一维省掉，每次DP完一个质因子用另一个数组记录第 $k$ 层的答案，即可做到空间复杂度 $O(\log^2 n~+~k~\log n)$。（其实动态开DP数组可以做到空间复杂度 $O(k~\log n)$，但是没啥意义）

最后统计答案时直接爆搜因数即可。

Code

#include <cstdio>

#include <cstring>

#include <vector>

#ifdef ONLINE_JUDGE

#define freopen(a, b, c)

#endif

#define rg register

#define ci const int

#define cl const long long

typedef long long ll;

namespace IPT {

    const int L = 1000000;

    char buf[L], *front=buf, *end=buf;

    char GetChar() {

	    if (front == end) {

		    end = buf + fread(front = buf, 1, L, stdin);

		    if (front == end) return -1;

		}

	    return *(front++);

	}

}

template <typename T>

inline void qr(T &x) {

    rg char ch = IPT::GetChar(), lst = ' ';

    while ((ch > '9') || (ch < '0')) lst = ch, ch=IPT::GetChar();

    while ((ch >= '0') && (ch <= '9')) x = (x << 1) + (x << 3) + (ch ^ 48), ch = IPT::GetChar();

    if (lst == '-') x = -x;

}

template <typename T>

inline void ReadDb(T &x) {

    rg char ch = IPT::GetChar(), lst = ' ';

    while ((ch > '9') || (ch < '0')) lst = ch, ch = IPT::GetChar();

    while ((ch >= '0') && (ch <= '9')) x = x * 10 + (ch ^ 48), ch = IPT::GetChar();

    if (ch == '.') {

	    ch = IPT::GetChar();

	    double base = 1;

	    while ((ch >= '0') && (ch <= '9')) x += (ch ^ 48) * ((base *= 0.1)), ch = IPT::GetChar();

	}

    if (lst == '-') x = -x;

}

namespace OPT {

    char buf[120];

}

template <typename T>

inline void qw(T x, const char aft, const bool pt) {

    if (x < 0) {x = -x, putchar('-');}

    rg int top=0;

    do {OPT::buf[++top] = x % 10 + '0';} while (x /= 10);

    while (top) putchar(OPT::buf[top--]);

    if (pt) putchar(aft);

}

const int maxt = 60;

const int maxm = 10010;

const int MOD = 1000000007;

ll n, kk, ans;

ll frog[maxm][maxt], inv[maxt], gorf[maxt][maxt], sum[maxm][maxt];

std::vector<ll> d;

int cnt;

int c[maxt];

void Get_Inv(ci, ci);

void dfs(ci, ci);

int mpow(cl x, int);

signed main() {

    freopen("1.in", "r", stdin);

    qr(n); qr(kk);

    Get_Inv(59, MOD);

    ll dn = n;d.push_back(0);

    for (ll i = 2; (i * i) <= n; ++i) if(!(dn % i)) {

	    d.push_back(i); ++cnt;

	    while (!(dn % i)) {dn /= i; ++c[cnt];}

	}

    if (dn != 1) {++cnt; d.push_back(dn); c[cnt] = 1;}

    for (rg int j = 1; j <= cnt; ++j) {

	    frog[0][c[j]] = sum[0][c[j]] = inv[c[j] + 1];

	    for (rg int i = 0; i < c[j]; ++i) frog[0][i] = 0, sum[0][i] = sum[0][c[j]];

	    for (rg int i = 1; i <= kk; ++i) {

		    rg int di = i - 1;

		    sum[i][c[j] + 1] = 0;

		    for (rg int k = c[j]; ~k; --k) {

			    frog[i][k] = sum[di][k];

			    sum[i][k] = (sum[i][k + 1] + frog[i][k] * inv[k + 1] % MOD) % MOD;

			}

		}

	    for (rg int k = 0; k <= c[j]; ++k) gorf[j][k] = frog[kk][k];

	}

    dfs(1, 1);

    qw((ans + MOD) % MOD, '\n', true);

    return 0;

}

void Get_Inv(ci x, ci p) {

    inv[1] = 1;

    for (rg int i = 2; i <= x; ++i) inv[i] = - p / i * inv[p % i] % MOD;

}

void dfs(ci cur, ci v) {

    if (cur > cnt) {ans = (ans + v) % MOD; return;}

    for (int i = 0; i <= c[cur]; ++i) dfs(cur + 1, 1ll * gorf[cur][i] * v % MOD * mpow(d[cur], i) % MOD);

}

int mpow(cl x, int y) {

    ll _ret = 1, _temp = x % MOD;

    while (y) {

	    if (y & 1) _ret = _ret * _temp % MOD;

	    _temp = _temp * _temp % MOD;

	    y >>= 1;

	}

	return _ret;

}