POJ3233_Matrix Power Series_矩阵幂_C++

　　题目：http://poj.org/problem?id=3233

　　这是今天考试的题目，结果没想出来写了个暴力30分，看完题解之后觉得自己是SB

　　

　　首先暴力就是一个个乘然后相加，时间是O(kn³)，极限数据要跑一个月才跑得出来

　　我们思考，求幂的话有快速幂（不会快速幂戳这里： http://www.cnblogs.com/hadilo/p/5719139.html ），那么矩阵一样也是可以的是不是

　　因为对于方阵A来说，(A²)²=A⁴

　　于是实数怎样做快速幂，矩阵就怎样做

 while (m>)
     {
         if (m%) mult(b,a);
         m/=;
         mult(a,a);
     }

　　手写一个 mult 函数，就用最普通的 n³ 矩阵乘法

　 （矩阵的基本运算，通俗易懂 http://www.cnblogs.com/hadilo/p/5865541.html）

 void mult(int x[N][N],int y[N][N])
 {
     int i,j,k;
     for (i=;i<=n;i++)
         for (j=;j<=n;j++)
             {
                 c[i][j]=;
                 for (k=;k<=n;k++) c[i][j]=(c[i][j]+x[i][k]*y[k][j])%mo;
             }
     for (i=;i<=n;i++)
         for (j=;j<=n;j++) x[i][j]=c[i][j];
 }

　　但题目要求的是 A+A²+...+A^k，而不是单个矩阵的幂

　　那么我们可以构造一个分块的辅助矩阵 S，其中 A 为原矩阵，E 为单位矩阵，O 为0矩阵

　　

　　我们将 S 取幂，会发现一个特性

　　

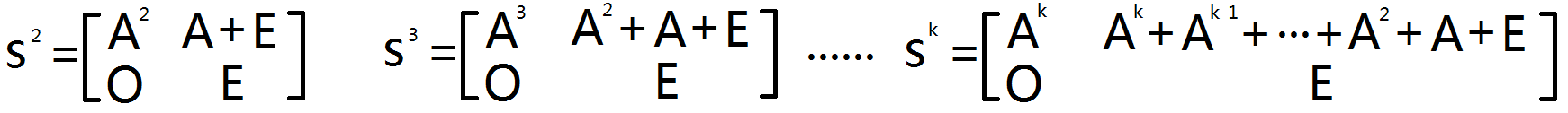
　　S^k 右上角那一块不正是我们要求的 A+A²+...+A^k 吗？

　　于是我们构造出 S 矩阵，然后对它求矩阵快速幂即可，最后别忘了减去一个单位阵

　　时间降为O(n³log₂k)，从一个月到0.8秒的跨越

 #include<algorithm>
 #include<iostream>
 #include<cstdlib>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 using namespace std;

 const int N=;
 int c[N][N],a[N][N],b[N][N],n,mo;
 void mult(int x[N][N],int y[N][N])
 {
     int i,j,k;
     for (i=;i<=n;i++)
         for (j=;j<=n;j++)
             {
                 c[i][j]=;
                 for (k=;k<=n;k++) c[i][j]=(c[i][j]+x[i][k]*y[k][j])%mo;
             }
     for (i=;i<=n;i++)
         for (j=;j<=n;j++) x[i][j]=c[i][j];
 }
 int main()
 {
     int m,i,j;
     scanf("%d%d%d",&n,&m,&mo);
     for (i=;i<=n;i++)
         {
             for (j=;j<=n;j++) scanf("%d",&a[i][j]);
             a[i][i+n]=a[i+n][i+n]=b[i][i]=b[i+n][i+n]=;
         }
     n*=;
     m++;
     while (m>)
         {
             if (m%) mult(b,a);
             m/=;
             mult(a,a);
         }
     n/=;
     for (i=;i<=n;i++) b[i][i+n]--;
     for (i=;i<=n;i++)
         {
             for (j=;j<n;j++) printf("%d ",b[i][j+n]);
             printf("%d\n",b[i][j+n]);
         }
     return ;
 }

版权所有，转载请联系作者，违者必究

QQ：740929894