UVa 1343 The Rotation Game (状态空间搜索 && IDA*)

题意：有个＃字型的棋盘，2行2列，一共24个格。

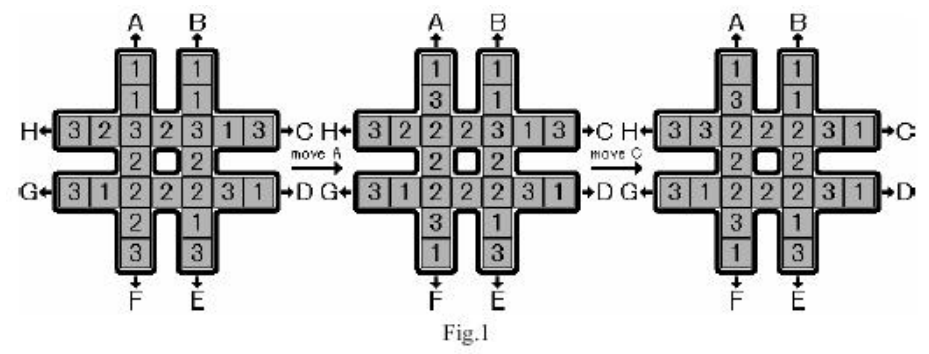
如图：每个格子是1或2或3，一共8个1，8个2，8个3.

有A~H一共8种合法操作，比如A代表把A这一列向上移动一个，最上面的格会补到最下面。

求：使中心8个格子数字一致的最少步骤，要输出具体的操作步骤及最终中心区域的数字。如果有多个解，输出字典序最小的操作步骤。

分析 ： 还是状态空间的搜索，对象就是一个数字序列，判断中心位置是否一样，可以看出如果使用BFS，每一层还是爆炸，所以使用IDA*，关键还是模拟操作和h函数，这里的h函数是这样定义的，可以看出每一次操作，最多给当前局面添加一个符合要求的数字，那就统计一下中心区域最多的相同数字有多少，然后如果8-h > max_depth - cur_depth的话代表最好的情况下都无法解决，剪枝。模拟操作应该就是很白痴的数组转移赋值了，代码很长，很烦，建议看看刘汝佳的代码。

#include<bits/stdc++.h>
using namespace std;
];
int ans_num;
];
bool Is_ok(int *arr)
{
    ];
    ] || temp!=arr[] || temp!=arr[] || temp!=arr[] || temp!=arr[] || temp!=arr[] || temp!=arr[])
        return false;
    return true;
}

inline int h(const int *now)
{
    ];
    memset(cnt, , sizeof(cnt));
    cnt[now[]]++,  cnt[now[]]++,  cnt[now[]]++,
    cnt[now[]]++, cnt[now[]]++, cnt[now[]]++,
    cnt[now[]]++, cnt[now[]]++;
    ], cnt[]);
    ret = max(ret, cnt[]);
    return ret;
}

inline void Change(int *tmp, int one, int two, int three, int four, int five, int six, int seven)
{
    ];
    index[] = one, index[] = two, index[] = three,
    index[] = four, index[] = five, index[] = six;
    index[] = seven;
    int temp = tmp[one];//!
    ; i<; i++)
        tmp[index[i]] = tmp[index[i+]];
    tmp[index[]] = temp;
}

bool DFS(int *now, int cur_depth, int max_depth, int per_dir)
{
     - h(now) > max_depth - cur_depth) return false;
    if(cur_depth >= max_depth) return false;//!?
    ; dir<=; dir++){//!
        ];
        ){
            &&dir==) || (dir==&&per_dir==)) continue;
            &&dir==) || (dir==&&per_dir==)) continue;
            &&dir==) || (dir==&&per_dir==)) continue;
            &&dir==) || (dir==&&per_dir==)) continue;
        }
        ; i<; i++) tmp[i] = now[i];
        int top = cur_depth;
        switch(dir){
            : ans[top]=,,,,,,);break;
            : ans[top]=,,,,,,);break;
            : ans[top]=,,,,,,);break;
            : ans[top]=,,,,,,);break;
            : ans[top]=,,,,,,);break;
            : ans[top]=,,,,,,);break;
            : ans[top]=,,,,,,);break;
            : ans[top]=,,,,,,);break;
        }
        if(Is_ok(tmp)){
            ans[top+] = '\0';
            ans_num = tmp[];
            return true;
        }
        , max_depth, dir)) return true;
    }
    return false;
}
int main(void)
{
    ]) && Init[]){
        ; i<=; i++){
            scanf("%d", &Init[i]);
        }
        if(Is_ok(Init)){
            puts("No moves needed");
            printf(]);
            continue;
        }
        ;
        ){
            , max_depth, )) break;
            max_depth++;
        }
        puts(ans);
        printf("%d\n", ans_num);
    }
    ;
}

刘汝佳代码：

// UVa1343 The Rotation Game
// Rujia Liu
// This solutions uses IDA* instead of BFS described in the book, because it's shorter 8-)
// It's shorter because no need for lookup tables and "automatically" lexicographically smallest solution.
#include<cstdio>
#include<algorithm>
using namespace std;

/*
      00    01
      02    03
04 05 06 07 08 09 10
      11    12
13 14 15 16 17 18 19
      20    21
      22    23
*/

// lines E~H are computed with the help of rev[]
][]={
  { , , ,,,,}, // A
  { , , ,,,,}, // B
  {, , , , , , }, // C
  {,,,,,,}, // D
};

] = {, , , , , , , }; // reverse lines of each line

// center squares
] = {, , , , , , , };

];
];

bool is_final() {
  ; i < ; i++)
    ]]) return false;
  return true;
}

int diff(int target) {
  ;
  ; i < ; i++)
    if(a[center[i]] != target) ans++;
  return ans;
}

inline int h() {
  ), diff()), diff());
}

inline void move(int i) {
  ]];
  ; j < ; j++) a[line[i][j]] = a[line[i][j+]];
  a[line[i][]] = tmp;
}

bool dfs(int d, int maxd) {
  if(is_final()) {
    ans[d] = '\0';
    printf("%s\n", ans);
    return true;
  }
  if(d + h() > maxd) return false;
  ; i < ; i++) {
    ans[d] = 'A' + i;
    move(i);
    , maxd)) return true;
    move(rev[i]);
  }
  return false;
}

int main() {
  ; i < ; i++)
    ; j < ; j++) line[i][j] = line[rev[i]][-j];
  ]) ==  && a[]) {
    ; i < ; i++) scanf("%d", &a[i]);
    ; i < ; i++) ;
    if(is_final()) {
      printf("No moves needed\n");
    } else {
      ; ; maxd++)
        , maxd)) break;
    }
    printf(]);
  }
  ;
}

瞎：遇到这种看起来很烦的题目，还是没有那种敏感性去试想状态空间搜索，一来就是想着如何模拟，然后脑袋一团shit，思路根本没有，所以总结应该很重要了，提供了一个思考的方向在那里，真正应该思考的是如何去实现这道题所对应的模型，而不是乱想。