USACO4.1 Fence Loops【最小环&边->点转化】

数据不是很大，如果要转换为正常的那种建图方式的话，可以给点进行标号，用一个二维数组存这两条边相交的那个点的标号，方便处理。一定要注意不要同一个点使用不同的编号也不要不同的点使用同一个编号（这不是废话嘛）不展开。

想多说一下一种比较有意思的做法，就是把边看成点，把边权转化为点权。

这样的话，原本的最小环长就变成了一条路径上经过的所有点的点权之和啦。

大概，张这个样子吧:

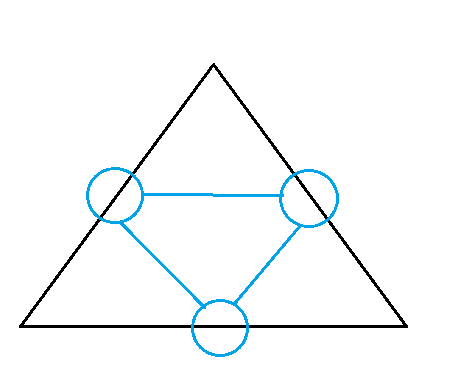
边是没有权值的，它只表示连通性。

不过由于把边看成了点，所以处理有些特殊：

原本的$dis[i][j]$是指点$i$到点$j$所经过的边权之和的最小值，但边->点之后，就变成了点$i$到点$j$所经过的点权之和的最小值（含点$i$和点$j$），那么在转移的时候，原本的方程式$dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j])$就不能用，因为$dis[i][k]$和$dis[k][j]$都包含了点$k$的点权，所以要减去，应该写成这个样子：

$$dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]-pw[k]/*point-weight*/)$$

然后就用$floyd$求最小环就可以了

->$break$ $in$ $something$

简单说一下$floyd$求最小环，感觉就是做一遍$floyd$答案就是$dis[i][i]$。

但是不行啊，因为无法保证$dis[i][k]$和$dis[k][j]$表示的路是不一样的。

转移的时候是枚举$i$,$j$,$k$三重循环的嘛，就在每一次通过$k$转移之前（也就是现在的$dis[i][j]$是靠$1~k$作为中转站转移过来的）对最小环进行更新，因为$dis[i][j]$和$i->k->j$走的路肯定不一样（一个肯定没有经过$k$，一个肯定经过了$k$）

就可以啦。

（如果你会$floyd$的话，上面的应该都能看懂，不过不会的话可以百度一下，$floyd$不是很难）

->$end$

另外，有一个很坑的地方，是由于边->点造成的，如果边长成这个样子：

那把边搞成点就成了这个样子：

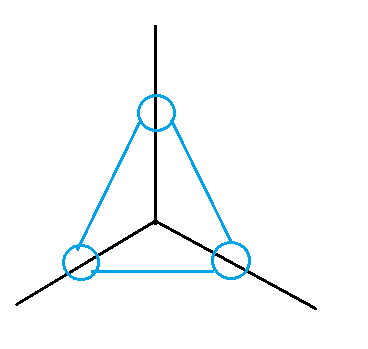
这是一个环，但是显然这个环是不符合题目要求的，因为题目要的是这种环：

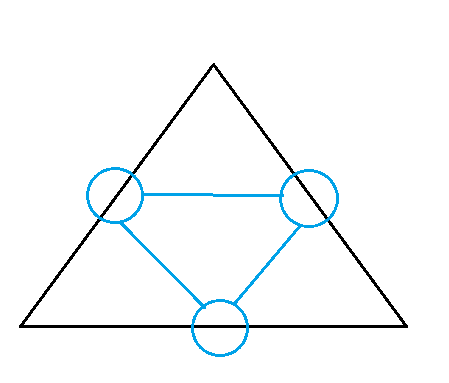
特判一下就可以啦，由于$N$只有$100$，随便怎么搞都可以。

 /*
 ID: Starry21
 LANG: C++
 TASK: fence6
 */
 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 using namespace std;
 #define N 105
 #define INF 0x3f3f3f3f
 int n,len[N]/*新图点权*/,ans=INF;
 int dis[N][N]/*两点间最短距离(floyd)*/,s[N][N]/*直接距离(直接相连的)*/;
 bool G[N][N]/*邻接矩阵*/,vis[N][N][N]/*判断三条边是否交于一点*/;
 int tmp[N],ns[];//辅助输入，见程序
 int main()
 {
     //freopen("fence6.in","r",stdin);
     //freopen("fence6.out","w",stdout);
     scanf("%d",&n);
     for(int p=;p<=n;p++)
     {
         int id;scanf("%d",&id);
         tmp[]=id;
         scanf("%d %d %d",&len[id],&ns[],&ns[]);
         for(int q=;q<=;q++)
         {
             for(int i=;i<=ns[q];i++)
             {
                 int id2;scanf("%d",&id2);
                 G[id][id2]=G[id2][id]=;
                 tmp[i]=id2;//记录边交于一点的编号
                 for(int j=;j<i;j++)
                     for(int k=;k<j;k++)
                         vis[tmp[i]][tmp[j]][tmp[k]]=vis[tmp[i]][tmp[k]][tmp[j]]=vis[tmp[j]][tmp[i]][tmp[k]]=vis[tmp[j]][tmp[k]][tmp[i]]=vis[tmp[k]][tmp[i]][tmp[j]]=vis[tmp[k]][tmp[j]][tmp[i]]=;
             }
         }
     }
     memset(dis,0x3f,sizeof(dis));
     for(int i=;i<=n;i++)
         for(int j=i+;j<=n;j++)
             if(G[i][j])
                 dis[i][j]=dis[j][i]=s[i][j]=s[j][i]=len[i]+len[j];
     for(int k=;k<=n;k++)
     {
         for(int i=;i<=n;i++)
             if(G[i][k])
                 for(int j=i+;j<=n;j++)
                     if(G[k][j]&&!vis[i][j][k])
                         ans=min(ans,dis[i][j]+s[i][k]+s[k][j]-len[i]-len[j]-len[k]);
         for(int i=;i<=n;i++)
             for(int j=;j<=n;j++)
                 dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]-len[k]);
     }
     printf("%d\n",ans);
     return ;
 }

Code