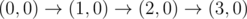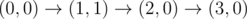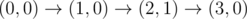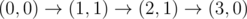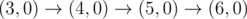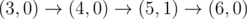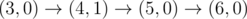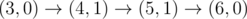Codeforces Round #420 (Div. 2) E. Okabe and El Psy Kongroo dp+矩阵快速幂

E. Okabe and El Psy Kongroo

 

Okabe likes to take walks but knows that spies from the Organization could be anywhere; that's why he wants to know how many different walks he can take in his city safely. Okabe's city can be represented as all points (x, y) such that x and y are non-negative. Okabe starts at the origin (point (0, 0)), and needs to reach the point (k, 0). If Okabe is currently at the point (x, y), in one step he can go to (x + 1, y + 1), (x + 1, y), or (x + 1, y - 1).

Additionally, there are n horizontal line segments, the i-th of which goes from x = ai to x = bi inclusive, and is at y = ci. It is guaranteed that a1 = 0, an ≤ k ≤ bn, and ai = bi - 1 for 2 ≤ i ≤ n. The i-th line segment forces Okabe to walk with y-value in the range 0 ≤ y ≤ ciwhen his x value satisfies ai ≤ x ≤ bi, or else he might be spied on. This also means he is required to be under two line segments when one segment ends and another begins.

Okabe now wants to know how many walks there are from the origin to the point (k, 0) satisfying these conditions, modulo 109 + 7.

Input

The first line of input contains the integers n and k (1 ≤ n ≤ 100, 1 ≤ k ≤ 1018) — the number of segments and the destination xcoordinate.

The next n lines contain three space-separated integers ai, bi, and ci (0 ≤ ai < bi ≤ 1018, 0 ≤ ci ≤ 15) — the left and right ends of a segment, and its y coordinate.

It is guaranteed that a1 = 0, an ≤ k ≤ bn, and ai = bi - 1 for 2 ≤ i ≤ n.

Output

Print the number of walks satisfying the conditions, modulo 1000000007 (109 + 7).

Examples

input

1 3
0 3 3

output

4

input

2 6
0 3 0
3 10 2

output

4

Note

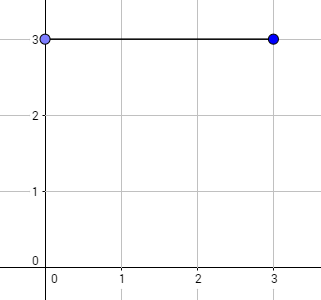
The graph above corresponds to sample 1. The possible walks are:

• 
• 
• 
• 

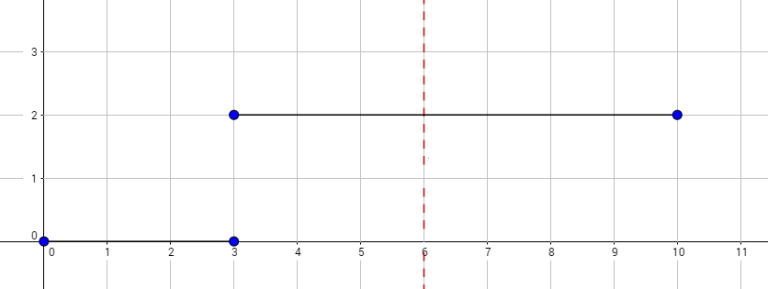
The graph above corresponds to sample 2. There is only one walk for Okabe to reach (3, 0). After this, the possible walks are:

• 
• 
• 
• 

题意就是让你从(0,0)点走到(k,0)点，有多少种方法，如果你在(x,y)点，你的下一步可以走(x+1, y+1), (x+1,y), 或者 (x+1, y-1).

有几条首尾在x坐标刚好相接的检测线，你在每一个检测线的底下不能超过任何一条检测线的y坐标

网上的大佬看了看数据范围就知道是递推+矩阵快速幂了...

套路题？？

果然我还是见得太少了，感觉看完这个题以后思路还是挺妙的利用矩阵快速幂来对递推进行优化

网上盗了一张图，权侵删...

代码如下：

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const ll mod=;
 typedef struct Matrix
 {
     ll mat[][];
 }matrix;
 matrix A,B,pre;
 ll n,endd;
 ll L,R,y;
 Matrix matrix_mul(matrix a,matrix b,ll len)
 {
     matrix c;
     memset(c.mat,,sizeof (c.mat));
     for (ll i=;i<=len;++i){
         for (ll j=;j<=len;++j){
             for (ll k=;k<=len;++k){
                 c.mat[i][j]+=((a.mat[i][k])%mod*(b.mat[k][j])%mod)%mod;
                 c.mat[i][j]%=mod;
             }
         }
     }
     return c;
 }
 Matrix matrix_quick_power(matrix a,ll k,ll len)
 {
     matrix b;
     memset(b.mat,,sizeof(b.mat));
     for (ll i=;i<=len;++i){
         b.mat[i][i]=;//单位矩阵
     }
     while (k){
         if (k%==){
             b=matrix_mul(a,b,len);
             k-=;
         }
         else{
             a=matrix_mul(a,a,len);
             k/=;
         }
     }
     return b;
 }
 int main(){
     while (cin>>n>>endd){
         memset(pre.mat,,sizeof (pre.mat));
         memset(A.mat,,sizeof (A.mat));
         for (ll i=;i<;++i){
             for (ll j=i-;j<i+&&j<;++j){
                 if (j>=&&j<=){
                     A.mat[i][j]=;
                 }
             }
         }
         ll flag=;
         pre.mat[][]=;
         for (ll i=;i<=n;++i){
             cin>>L>>R>>y;//读入每个线段
             if (R>endd) R=endd,flag=;//如果边界超出了结束的节点就不用多算了
             B=matrix_quick_power(A,R-L,y);//让A那个矩阵做一下快速幂
             for (ll j=y+;j<=;++j) pre.mat[j][]=;
             //trick,如果上一个线段结束时有高于当前线段的起点的部分,这一部分是不能走的，我们把pre的这部分附为0
             B=matrix_mul(B,pre,y);
             for (ll j=;j<=y;++j)
                 pre.mat[j][]=B.mat[j][];//我们每次更新一下第一列
             if (flag==)
                 break;
         }
         cout<<B.mat[][]<<endl;
     }
 }