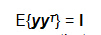独立成分分析(Independent Component Analysis)
ICA是一种用于在统计数据中寻找隐藏的因素或者成分的方法。ICA是一种广泛用于盲缘分离的(BBS)方法,用于揭示随机变量或者信号中隐藏的信息。ICA被用于从混合信号中提取独立的信号信息。ICA在20世纪80年代提出来,但是知道90年代中后期才开始逐渐流行起来。
ICA的起源可以来源于一个鸡尾酒会问题,我们假设三个观测点x1,x2,x3,放在房间里同时检测三个人说话,另三个人的原始信号为s1,s2,s3,则求解的过程可以如下图所示:
定义
假设n个随机变量x1,x2,….xn,由n个随机变量s1,s2,…sn组成,并且这n个随机变量是相互独立的,可以用下面的公示表达:
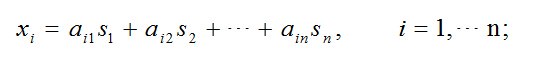
为了表达的方便,我们可以用向量的形式来表达:
x = As
这个只不过是ICA最基本的定义,在很多实际问题中,应该包含了噪声。但是为了简化问题,我们这里忽略了噪声。因为如果模型中包含噪音,处理起来将会十分困难,而且大多数不包含噪音的模型已经能够解决很多问题,所以这里我们就将噪声先忽略。
ICA的限制条件
- 独立成分应该是相互之间独立的。这是ICA成立的基本原则,同时,基本上可以说只需要这个原则我们就可以估计这个模型。
- 独立成分必须是非高斯分布的。高斯分布的高阶累计量是0,但是高阶信息对于ICA的模型的估计却是十分必要的。
- 为了简化,我们假设未知的混合矩阵A是一个方阵。
白化
白化是一种比不相关性要稍微强一些的性质。对一个零均值的随即向量y进行白化处理,就是让它的组成成分不相关,并且让变量的方差相等。也就是说,变量y的协方差矩阵是单位矩阵:
为什么独立成分是非高斯的
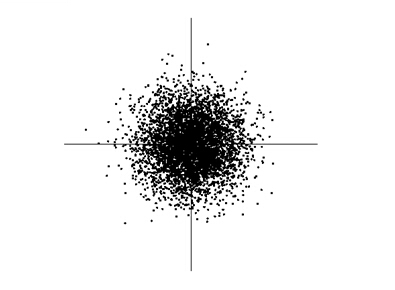
ICA最基本的限制条件就是独立成分必须是非高斯分布的,这或许也是ICA早期没有流行起来的原因。我们假设变量x1和x2是高斯分布的,不相关的,且方差相等:
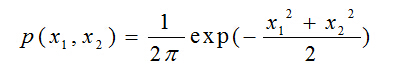
下面的图表示联合概率分布,可以看出,我们无法判断任何关于变量x1和x2的方向信息,这就是为什么混合矩阵A不能被估计出来的原因:
峭度
在这我们讲述一个利用峭度来进行ICA模型估计的方法,ICA的估计方法很多,这只是最基础的一个方法。
对于变量y峭度可以由下面的公式定义:
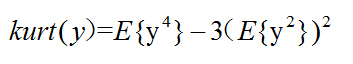
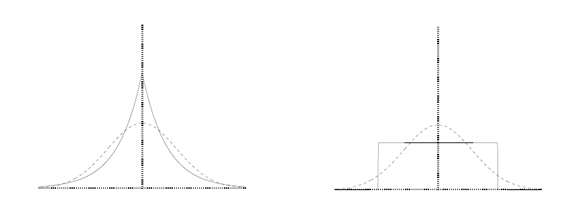
峭度是可正可负的,高斯分布变量的峭度是0,这也是为什么独立成分必须是非高斯分布的原因之一。峭度为负的变量分布称为次高斯分布,峭度为正的变量的分布则为超高斯分布,下图分别是拉普拉斯分布(超高斯分布)和均匀分布(次高斯分布):
基于峭度的梯度算法
我们经常利用峭度的绝对值或者平方来进行求解:
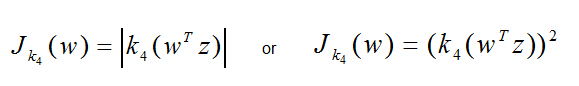
我们通过优化这个目标函数来估计ICA模型,z表示白化后的观察数据x。
实际上,我们是使峭度极大化。我们会从某个方向向量w开始,然后计算在什么方向峭度的增长最快,我们则将方向向量w向这个方向移动。
峭度绝对值的梯度可以如下计算:
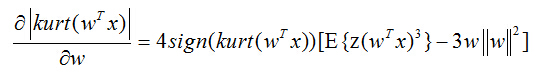
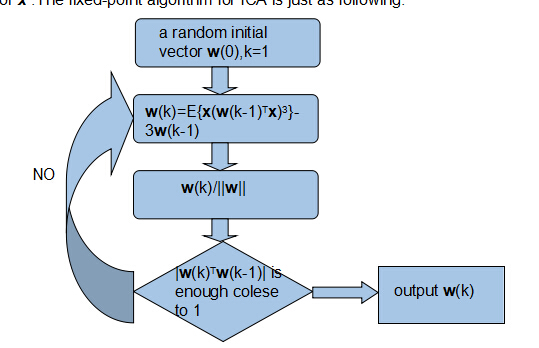
下面是一个快速不动点算法基于峭度计算的流程图:
## ICA估计的主要方法 ##
- 通过极大化非高斯性来估计
- 通过极大似然性来估计
- 通过极小互信息来估计
- 通过张量的方法来估计
- 通过非线性分解和非线性PCA来估计
这里,我们只是讲了其中的一个基础方法之一,并不就是最好的方法。
ICA算法的思想可以用下面的公式来描述:
ICA method = objective funtion + optimization algorithm
引用
[1]Hyvärinen A, Karhunen J, Oja E. Independent component analysis[M]. John Wiley & Sons, 2004.
[2]Hyvärinen A, Oja E. Independent component analysis: algorithms and applications[J]. Neural networks, 2000, 13(4): 411-430.
[3]Hyvärinen A, Oja E. A fast fixed-point algorithm for independent component analysis[J]. Neural computation, 1997, 9(7): 1483-1492.
[4]王刚. 基于最大非高斯估计的独立分量分析理论研究 [D][D]. 国防科学技术大学, 2005.
独立成分分析(Independent Component Analysis)的更多相关文章
- 斯坦福ML公开课笔记15—隐含语义索引、神秘值分解、独立成分分析
斯坦福ML公开课笔记15 我们在上一篇笔记中讲到了PCA(主成分分析). PCA是一种直接的降维方法.通过求解特征值与特征向量,并选取特征值较大的一些特征向量来达到降维的效果. 本文继续PCA的话题, ...
- 机器学习 —— 基础整理(四)特征提取之线性方法:主成分分析PCA、独立成分分析ICA、线性判别分析LDA
本文简单整理了以下内容: (一)维数灾难 (二)特征提取--线性方法 1. 主成分分析PCA 2. 独立成分分析ICA 3. 线性判别分析LDA (一)维数灾难(Curse of dimensiona ...
- Topographic ICA as a Model of Natural Image Statistics(作为自然图像统计模型的拓扑独立成分分析)
其实topographic independent component analysis 早在1999年由ICA的发明人等人就提出了,所以不算是个新技术,ICA是在1982年首先在一个神经生理学的背景 ...
- PCA主成分分析 ICA独立成分分析 LDA线性判别分析 SVD性质
机器学习(8) -- 降维 核心思想:将数据沿方差最大方向投影,数据更易于区分 简而言之:PCA算法其表现形式是降维,同时也是一种特征融合算法. 对于正交属性空间(对2维空间即为直角坐标系)中的样本点 ...
- 独立成分分析 ICA 原理及公式推导 示例
独立成分分析(Independent component analysis) 前言 独立成分分析ICA是一个在多领域被应用的基础算法.ICA是一个不定问题,没有确定解,所以存在各种不同先验假定下的求解 ...
- ICA (独立成分分析)
介绍 独立成分分析(ICA,Independent Component Correlation Algorithm)简介 X=AS X为n维观测信号矢量,S为独立的m(m<=n)维未知源信号矢量 ...
- Independent Components Analysis:独立成分分析
一.引言 ICA主要用于解决盲源分离问题.需要假设源信号之间是统计独立的.而在实际问题中,独立性假设基本是合理的. 二.随机变量独立性的概念 对于任意两个随机变量X和Y,如果从Y中得不到任何关于X的信 ...
- ICA(独立成分分析)笔记
ICA又称盲源分离(Blind source separation, BSS) 它假设观察到的随机信号x服从模型,其中s为未知源信号,其分量相互独立,A为一未知混合矩阵. ICA的目的是通过且仅通过观 ...
- 独立成分分析(Independent component analysis, ICA)
作者:桂. 时间:2017-05-22 12:12:43 链接:http://www.cnblogs.com/xingshansi/p/6884273.html 前言 今天群里冒出这样一个问题:群里谁 ...
随机推荐
- 自定义线程池的名称(ThreadPoolExecutor)
目的:有时候为了快速定位出现错误的位置,在采用线程池时我们需要自定义线程池的名称. 1.创建ThreadFactory(ThreadPoolExecutor默认采用的是DefaultThreadFac ...
- mysql 5.7以上版本下载及安装
一.下载 1.mysql官网下载地址:https://downloads.mysql.com/archives/community/ 2.下载完成后解压,解压后如图: 3.放置位置,把解压好的文件夹放 ...
- hdu 6055 : Regular polygon (2017 多校第二场 1011) 【计算几何】
题目链接 有个结论: 平面坐标系上,坐标为整数的情况下,n个点组成正n边形时,只可能组成正方形. 然后根据这个结论来做. 我是先把所有点按照 x为第一关键字,y为第二关键字 排序,然后枚举向量 (p[ ...
- HashMap测试程序2
package com.iotek.map; import java.util.HashMap;import java.util.Map; public class HashMapDemo2 { /* ...
- asp.net中的ORA-12154: TNS: 无法解析指定的连接标识符
本机PL/SQL能正常连接,但是asp.net连接有问题. 临时解决方案: <add key="ConnectString" value="Data Source= ...
- 浅谈MySQL优化
本文整理了一些MySQL的通用优化方法,做个简单的总结分享,旨在帮助那些没有专职MySQL DBA的企业做好基本的优化工作,至于具体的SQL优化,大部分通过加适当的索引即可达到效果,更复杂的就需要具体 ...
- Leetcode_1278. Palindrome Partitioning III_[DP]
题目链接 You are given a string s containing lowercase letters and an integer k. You need to : First, ch ...
- mysql 1067 - Invalid default value for 'addtime'错误处理
错误描述 TABLE `bota_payment_closing` ( `id` int(11) NOT NULL AUTO_INCREMENT, `monthly` varchar(8) NOT N ...
- 数据库的目录IDF打不开!附加失败
选择附加数据库,结果 武汉地图打不开 这是mapgis k9里面自带的地图 IDF:Identity Definition File?https://zhidao.baidu.com/question ...
- Nexus Repository OSS 3安装配置使用
Nexus Repository OSS 3是一个开源的仓库管理系统,提供了更加丰富的功能,而且安装.配置.使用起来也更加简单方便.OSS 3版本主要支持的仓库(Repository)包括如下: bo ...