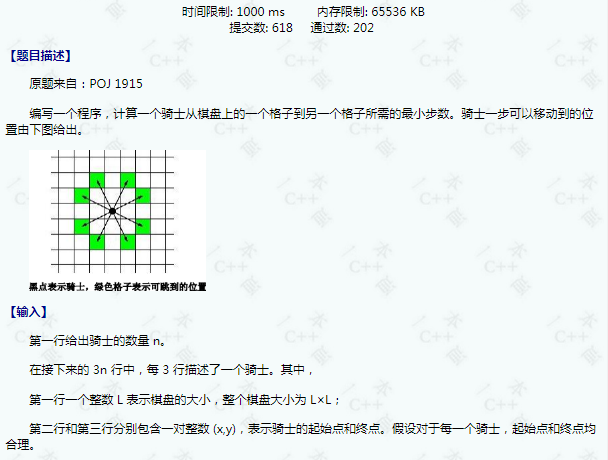
1450：【例 3】Knight Moves

1450：【例 3】Knight Moves

 题解

这道题可以用双向宽度搜索优化（总介绍在  BFS ）

给定了起始状态和结束状态,求最少步数,显然是用BFS,为了节省时间,选择双向BFS。

双向BFS,即从起点向终点搜,从终点向起点搜,扩展各自的状态,直到出现两者扩展的状态重合

优化:每次选择结点少的扩展

看一下骑士可以到达那些点呢？？

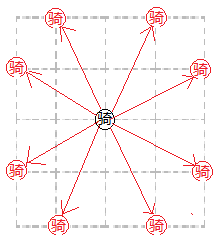
所以当然要开两个队列啦

设定：

1. dis[ i ][ a ][ b ]：队列 i ，从起点（a，b）至少多少步

2.    v[ i ][ a ][ b ]：队列 i ，从起点（a，b）开始，标记是否走过

3.           q[ i ][ j ]：队列 i 中第 j 个元素

4.                 l[ i ]：队列 i 的头指针

5.                 r[ i ]：队列 i 的尾指针

代码

1.优化版 双向队列

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<string>
#include<cstdlib>

using namespace std;

struct node
{
    int x,y;
}q[][];     //定义两个队列
int text,ans,n,l[],r[];
int dis[][][],v[][][];
int dx[]={-,-,-,-,,,,};    //位移
int dy[]={-,,-,,-,,-,};

int expand(int k)    //对队列 k 进行扩展
{
    int t,i,j,x,y,d,tx,ty;
    x=q[k][l[k]].x;
    y=q[k][l[k]].y;
    d=dis[k][x][y];
    for(int i=;i<;i++)  //八个方向扩展
    {
        tx=x+dx[i];    //新点
        ty=y+dy[i];

        if(tx>=&&tx<=n&&ty>=&&ty<=n&&!v[k][tx][ty])   //合法而且没走过
        {
            v[k][tx][ty]=;  //标记走过
            r[k]++;          //入队
            q[k][r[k]].x=tx;
            q[k][r[k]].y=ty;
            dis[k][tx][ty]=d+; //记录步数
            if(v[-k][tx][ty])
            //判断另一个队列中是否已经走过这个点，也就是判断是否重合相遇
            //如果相遇，就找到了一条完整的最短路径
            //k=0时，1-k=1
            //k=1时，1-k=0
            {
                ans=dis[k][tx][ty]+dis[-k][tx][ty];
                return ;
            }
        }
    }
    return ;
}

void bfs()
{
    if(q[][].x==q[][].x&&q[][].y==q[][].y) //起点终点本就相同
    {
        ans=;  return;
    }
    v[][q[][].x][q[][].y]=;  //标记走过
    v[][q[][].x][q[][].y]=;
    l[]=r[]=;    //初始化头指针尾指针
    l[]=r[]=;
    while(l[]<=r[]&&l[]<=r[])  //两个队列都非空，先扩展结点数少的
    {
        if(r[]-l[]<r[]-l[])
        {
           if(expand())  return;  //找到答案啦
           l[]++;   //QAQ 没找到，移动头指针继续找
        }
        if(r[]-l[]>=r[]-l[])
        {
            if(expand())  return;
            l[]++;
        }
    }

}

int main()
{
    scanf("%d",&text);
    for(int i=;i<=text;i++)  //多组数据
    {
        memset(dis,,sizeof(dis));
        memset(v,,sizeof(v));
        memset(q,,sizeof(q));

        scanf("%d",&n);  n=n-;
        scanf("%d%d",&q[][].x,&q[][].y);   //起点
        scanf("%d%d",&q[][].x,&q[][].y);   //终点
        bfs();
        printf("%d\n",ans);
    }

    return ;
}

2.普通队列

（应该不是代码的锅吧，写着写着卡死一台电脑，换了一台就没事了）

#include<bits/stdc++.h>

using namespace std;

struct node
{
    int x,y,step;
}s,e,now,next;

int cnt,n,ans;
bool vis[][];
int dx[]={-,-,-,-,,,,};
int dy[]={-,,-,,-,,-,};

bool pan(int x,int y)
{
    return x>=&&x<=n&&y>=&&y<=n&&!vis[x][y];
}

int bfs()
{
    queue<node>q;
    s.step =;
    q.push(s);
//    vis[s.x ][s.y ]=1;   //反正它还要被取出来
    while(!q.empty())
    {
        now=q.front();
        q.pop();
//        vis[now.x ][now.y ]=0;  //保证每个点都走一遍吧，不重复走点，不过要是加上的话，就超时了
        if(now.x ==e.x &&now.y ==e.y )  //到达终点
        {
            return now.step ;
            continue;
        }
        else
        {
            for(int i=;i<;i++)
            {
                next.x =now.x +dx[i];
                next.y =now.y +dy[i];
                if(pan(next.x ,next.y ))
                {
                    next.step =now.step +;
                    q.push(next);
                    vis[next.x ][next.y ]=;
                }
            }
        }
    }
    return ;
}

int main()
{
    scanf("%d",&cnt);
    for(int i=;i<=cnt;i++)
    {
        memset(vis,,sizeof(vis));

        scanf("%d",&n);
        scanf("%d%d",&s.x ,&s.y );
        scanf("%d%d",&e.x ,&e.y );

        if(s.x ==e.x &&s.y ==e.y )
        {
            printf("0\n");
            continue;
        }
        else
        {
            ans=bfs();
            printf("%d\n",ans);
        }
    }
    return ;
}