POJ 2676 Sudoku (DFS)
| Time Limit: 2000MS | Memory Limit: 65536K | |||
| Total Submissions: 11694 | Accepted: 5812 | Special Judge | ||
Description
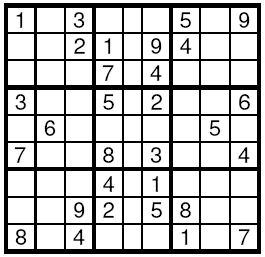
Input
Output
Sample Input
1
103000509
002109400
000704000
300502006
060000050
700803004
000401000
009205800
804000107
Sample Output
143628579
572139468
986754231
391542786
468917352
725863914
237481695
619275843
854396127
Source
大致题意:
九宫格问题,也有人叫数独问题
把一个9行9列的网格,再细分为9个3*3的子网格,要求每行、每列、每个子网格内都只能使用一次1~9中的一个数字,即每行、每列、每个子网格内都不允许出现相同的数字。
0是待填位置,其他均为已填入的数字。
要求填完九宫格并输出(如果有多种结果,则只需输出其中一种)
如果给定的九宫格无法按要求填出来,则输出原来所输入的未填的九宫格
解题思路:
DFS试探,失败则回溯
用三个数组进行标记每行、每列、每个子网格已用的数字,用于剪枝
bool row[10][10]; //row[i][x] 标记在第i行中数字x是否出现了
bool col[10][10]; //col[j][y] 标记在第j列中数字y是否出现了
bool grid[10][10]; //grid[k][x] 标记在第k个3*3子格中数字z是否出现了
row 和 col的标记比较好处理,关键是找出grid子网格的序号与 行i列j的关系
即要知道第i行j列的数字是属于哪个子网格的
首先我们假设子网格的序号如下编排:
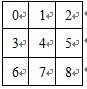
由于1<=i、j<=9,我们有: (其中“/”是C++中对整数的除法)
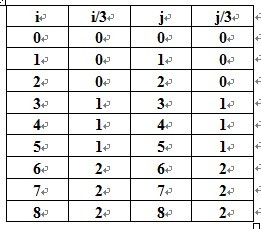
令a= i/3 , b= j/3 ,根据九宫格的 行列 与 子网格 的 关系,我们有:
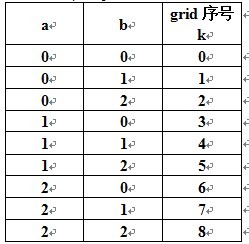
不难发现 3a+b=k
即 3*(i/3)+j/3=k
又我在程序中使用的数组下标为 1~9,grid编号也为1~9
因此上面的关系式可变形为 3*((i-1)/3)+(j-1)/3+1=k
有了这个推导的关系式,问题的处理就变得非常简单了,直接DFS即可
#include<iostream>
#include<cstdio>
#include<cstring> using namespace std; int map[][]; bool row[][]; //row[i][x] 标记在第i行中数字x是否出现了
bool col[][]; //col[j][y] 标记在第j列中数字y是否出现了
bool grid[][]; //grid[k][z ] 标记在第k个3*3子格中数字z是否出现了 bool DFS(int x,int y){
if(x==)
return true;
bool flag=false;
if(map[x][y]!=){
if(y==)
flag=DFS(x+,);
else
flag=DFS(x,y+);
//return flag;
if(flag) //回溯
return true;
else
return false;
}else{
int k=*((x-)/)+(y-)/+;
for(int i=;i<=;i++) //枚举数字1~9填空
if(!row[x][i] && !col[y][i] && !grid[k][i]){
map[x][y]=i;
row[x][i]=true;
col[y][i]=true;
grid[k][i]=true;
if(y==)
flag=DFS(x+,);
else
flag=DFS(x,y+);
if(flag) //回溯,继续枚举
return true;
else{
map[x][y]=;
row[x][i]=false;
col[y][i]=false;
grid[k][i]=false;
}
}
}
return false;
} int main(){ //freopen("input.txt","r",stdin); int t;
scanf("%d",&t); while(t--){
memset(row,false,sizeof(row));
memset(col,false,sizeof(col));
memset(grid,false,sizeof(grid));
char str[][];
for(int i=;i<=;i++){
//scanf("%s",str[i]+1); //为啥这样输入就不行了呢??纳闷ing,明天再弄吧
for(int j=;j<=;j++){
cin>>str[i][j];
map[i][j]=str[i][j]-'';
if(map[i][j]){
int k=*((i-)/)+(j-)/+;
row[i][map[i][j]]=true;
col[j][map[i][j]]=true;
grid[k][map[i][j]]=true;
}
}
}
DFS(,);
for(int i=;i<=;i++){
for(int j=;j<=;j++)
printf("%d",map[i][j]);
printf("\n");
}
}
return ;
}
下面这个很快:
#include <iostream>
#include<cstdio>
#include<cstring> using namespace std; int num,v[][],map[][];
//bool pd[10][10]; //判断输入的时候是否为零 bool judge(int x,int y,int k){
int i,j,it,jt;
for(i=;i<;i++){
if(map[i][y]==k) return false;
if(map[x][i]==k) return false;
}
it=(x/)*;
jt=(y/)*;
for(i=;i<;i++)
for(j=;j<;j++)
if(map[i+it][j+jt]==k)
return false;
return true;
} int dfs(int cap){
int i,x,y;
if(cap<) return ; for(i=;i<=;i++){
x=v[cap][];
y=v[cap][];
if(judge(x,y,i)){
map[x][y]=i;
if(dfs(cap-)) return ;
map[x][y]=;
}
}
return ;
} int main(){
int t,i,j;
char c;
scanf("%d\n",&t);
while(t--){
num=;
for(i=;i<;i++,getchar())
for(j=;j<;j++){
scanf("%c",&c);
map[i][j]=c-'';
if(map[i][j]==){ //将为空的点的坐标全部记录下来,等下需要用暴力解决
v[num][]=i;
v[num++][]=j;
}
}
dfs(num-);
for(i=;i<;i++){
for(j=;j<;j++)
printf("%d",map[i][j]);
printf("\n");
}
}
return ;
}
POJ 2676 Sudoku (DFS)的更多相关文章
- POJ 2676 Sudoku(深搜)
Sudoku Time Limit : 4000/2000ms (Java/Other) Memory Limit : 131072/65536K (Java/Other) Total Submi ...
- POJ 2676 Sudoku (数独 DFS)
Time Limit: 2000MS Memory Limit: 65536K Total Submissions: 14368 Accepted: 7102 Special Judg ...
- POJ 1190 生日蛋糕(DFS)
生日蛋糕 Time Limit: 1000MSMemory Limit: 10000KB64bit IO Format: %I64d & %I64u Submit Status Descrip ...
- poj2676 Sudoku(DFS)
做了很久还是参考了别人的答案orz,其实也不难啊.我要开始学一下怎么写搜索了... 题目链接:poj2676 Sudoku 题解:暴力搜索,DFS每个空白格子所放数字. #include<cst ...
- POJ - 3074 Sudoku (搜索)剪枝+位运算优化
In the game of Sudoku, you are given a large 9 × 9 grid divided into smaller 3 × 3 subgrids. For exa ...
- POJ 2531-Network Saboteur(DFS)
Network Saboteur Time Limit: 2000MS Memory Limit: 65536K Total Submissions: 9435 Accepted: 4458 ...
- 深搜+回溯 POJ 2676 Sudoku
POJ 2676 Sudoku Time Limit: 2000MS Memory Limit: 65536K Total Submissions: 17627 Accepted: 8538 ...
- POJ 3414 Pots(罐子)
POJ 3414 Pots(罐子) Time Limit: 1000MS Memory Limit: 65536K Description - 题目描述 You are given two po ...
- POJ 2431 Expedition(探险)
POJ 2431 Expedition(探险) Time Limit: 1000MS Memory Limit: 65536K [Description] [题目描述] A group of co ...
随机推荐
- Mahout 安装配置
http://log.medcl.net/item/2011/02/mahout_install/ Apache Mahout是一个机器学习的框架,构建在hadoop上支持大规模数据集的处理,目前最新 ...
- 如何在编辑器里添加CSS或JS代码
//编辑器里代码模式下的代码 <scripttype="text/javascript"> //my code.... </script> //编辑器里可视 ...
- 如何防止XSRF攻击
XSRF全称是 cross-site request forgery(跨站点请求伪造),也称为CSRF,是一种常见的web攻击方式. 攻击形式描述如下: 1.用户登录并访问一个正常的站点 http:/ ...
- Ubuntu 突然上不去网了怎么办
到家了也想看看程序.打开WIN8上的虚拟机VM,然后启动Ubuntu.................................... 像往常一样等待着界面,输入password,然后改动程序. ...
- 优化MySQL开启skip-name-resolve参数时显示“ignored in --skip-name-resolve mode.”Warning解决方法
转自:http://blog.csdn.net/yiluoak_47/article/details/53381282 参数用途: skip-name-resolve #禁止MySQL对外部连接进行D ...
- Objective-C编程 - 关于Block的要点
1. 首先,我们快速过一下,什么是Block? Block是一段代码,它在OC中以^开头,可以有返回值,和参数列表,但就是没有名字. 所以,你可以把它认为是匿名函数. 事实上,它和Swift中的闭包( ...
- Go语言使用Beego的ORM插入Mysql后,时区不一致的解决方案
一.解决方案: 方案一: orm.Debug = false orm.DefaultTimeLoc = time.UTC orm.RegisterDriver("mysql", o ...
- Unix线程概念、控制原语、属性
线程: 线程基础概念: 线程在Linux中又称轻量级进程.而且它和进程都有PCB(进程控制块).可是差别是进程的虚拟地址空间是独享的,也就是每一个进程都有自己的虚拟地址空间.可是线程的PCB是共享的, ...
- iframe 与 frame 区别
1.iframe iframe主要来内联一个外联的页面,如: <!DOCTYPE html> <html lang="zh"> <head> & ...
- POJ 2003 Hire and Fire (多重链表 树结构 好题)
Hire and Fire Time Limit: 1000MS Memory Limit: 30000K Total Submissions: 2316 Accepted: 655 Desc ...
