[Scikit-learn] 2.5 Dimensionality reduction - ICA

理论学习：

独立成分分析ICA历史

Ref: Lecture 15 | Machine Learning (Stanford) - NG

From: https://wenku.baidu.com/view/ad0973b94028915f804dc2aa.html

解ICA的若干种方法：

• ICA by Maximization of Nongaussianity       <----
• ICA by Maximum Likelihood Estimation　　<----
• ICA by Minimization of Mutual Information
• ICA by Tensorial Methods
• ICA by Nonlinear Decorrelation and Nonlinear PCA

---

ICA by Maximization of Nongaussianity

基本背景：

估值原理：

解决方案：

方法有很多，基本都是：度量方法+算法，比如 "negentropy近似" + "基于固定点迭代方法"。

与PCA的比较：

论文阅读杂记：ICA及其在数字图像处理中的应用

应用例子，特征提取方法 + svm 进行人脸识别

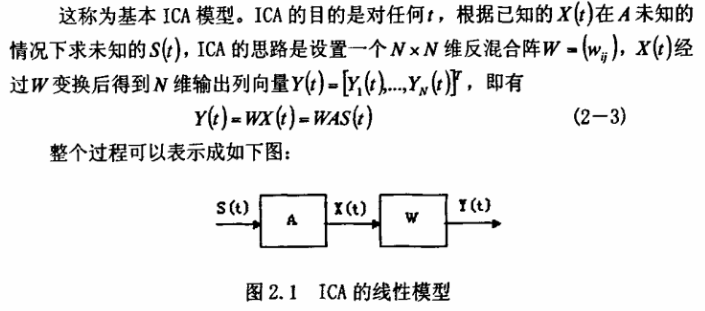
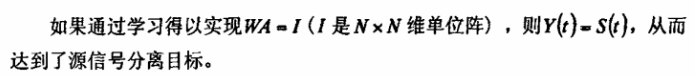
Centered and whitened

Ref: http://www.cnblogs.com/tornadomeet/archive/2013/03/21/2973231.html

优化方法

基于固定点迭代的方法：

看上去很像牛顿法，why?

ICA by Maximum Likelihood Estimation

Ref: Lecture 15 | Machine Learning (Stanford) - NG

From: ICA教程之一【推荐！】

记录随机向量X的值m次，则形成数据集：

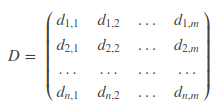
实例：在一个大厅里，有n个人在随机聊天。在大厅的不同角落，布置n个麦克风记录大厅的声音，每秒一个记录，一共记录m秒。

麦克风记录的混合声音，多个麦克风记录不同位置的混合声音。

ICA的目标，就是从混声录音中将每个人的声音分离出来。

得到的似然函数如下：

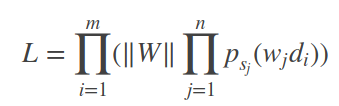
【m秒的记录，n个话筒】

这里就不多讲了，请见原链接，讲得比较清楚，建议自己推导一遍在本本上。

优化方法

Newton method：

Stochastic Gradient Ascent：