大规模向量相似度计算方法(Google在07年发表的文章)

转载请注明出处：http://www.cnblogs.com/zz-boy/p/3648878.html

更多精彩文章在：http://www.cnblogs.com/zz-boy/

最近看了Google在 WWW2007上发表的Scaling Up All Pairs Similarity Search，觉得还不错，分享一下作者的思路。

在基于用户协同过滤方法的推荐系统中，用户相似度的计算是最终推荐的基础步骤；用户向量是用户的行为向量，其每一维度是物品，值是用户对该物品的喜爱程度，这种场景尤其多见于电商网站，电商网站中的用户数据量是很大的，物品数量也很多，这就导致用户向量数量很大，如果不加优化的计算用户相似度，其时间开销是很大的。

我们给出相似度计算问题的定义：

有一个实数值向量集合U，x(v₁,…,v_n)是一个实数值向量且x属于U，相似度计算公式为sim(x,y)，最终我们要得到的是(x,y,sim(x,y))的集合，其中x，y都属于U，并且sim(x,y)>=t.

可能刚开始看到这个问题，我们的直观的想法都是下面的这种蛮力的求解方法：

上面的方法没有经过任何的优化，t的作用仅仅体现在计算完成的相似度是否满足约束，其实仔细思考这个问题，t的作用不应该仅仅局限于此，我们在将x放入I时，或许可以考虑x是否会和余下的向量相似。基于这样的想法于是便有了下面改进的算法：

可以看到在上面的算法中，很关键的一行是

maxweight_i(V)的含义是向量集合V中第i列的最大值，如果遍历完x，b的值仍然小于t，那么x就不可能和余下的向量相似，所以x就不应该被加入倒排表I。另外该算法开头部分对向量维度的重排，在该算法中看似没有什么效果，也就是说即使不重排，也不会影响算法的效率，要让开头语句起作用，上面的算法还要做一些小的改动，在循环

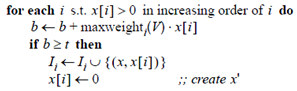
中，一旦判断出b>=t,那么式子

就不要再计算了，这样的改进如果能够提高效率是因为数据满足假设：

一个向量所有维的最大值出现在向量集合密集维度的可能性相对出现在稀疏维度更大。

这个假设不总是成立的，取决于数据集。

下面的算法对数据又加了一步预处理，将V集合按照maxweight(x)的降序排列。

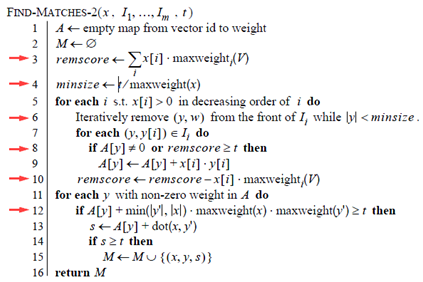
上面算法精彩的几点如下：

1. 

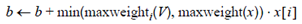
   后续将加入倒排表I的向量，所有维度的最大值必然小于maxweight(x)，因为数据预处理中的排序步骤。

2. 

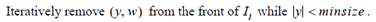
   推导步骤：

   如果|y|*maxweight(x)<t那么y必然不可能再和后续的要加入倒排表中的向量相似。

   这里还要解释一下的是既然All-PAIRS-2中已经对能否加入倒排表中的向量进行了更加严格的限制，这里为什么还要对I进行筛除，这主要是因为对y进行处理时，是针对余下的所有x，当到对x进行处理，和y相似的所有向量都在y至x的处理序列之间，即y不可能再和x之后的向量相似了，所以当处理时对y进行的一个粗的筛选。

3. remscore的作用主要体现在和语句

   

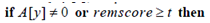
   的配合上，试想如果遍历到某一个i时，A[y]=0但是此时remscore却是小于t，那么必然有x不可能和y相似，所以也就没必要计算A[y]了。

4. 

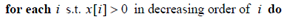
   此条语句是降序的原因：向量x的维度序列经过重排，当i降序时，维度稀疏性的变化为稀疏到密集，再结合语句

   

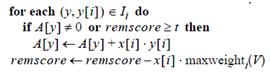
   便能做到最大限度的减少在密集维度中的计算次数。

更多精彩文章在：http://www.cnblogs.com/zz-boy/