Finite State Transducers

一， 简介

Finite State Transducers 简称 FST， 中文名：有穷状态转换器。在自然语言处理等领域有很大应用，其功能类似于字典的功能（STL 中的map，C# 中的Dictionary），但其查找是O（1）的，仅仅等于所查找的key长度。目前Lucene4.0在查找Term时就用到了该算法来确定此Term在字典中的位置。

FST 可以表示成FST<Key, Value>的形式，我们可以用O（length（key））的复杂度，找到key所对应的值。除此之外，FST 还支持用Value来查找key以及查找Value最优的key等功能。

FST 如此强大，但是目前网上对其讲解的资料很少，中文的就更是微乎其微了。

二，数据结构

FST 是一种类似于Trie或自动机的数据结构，所以在学习之前您一定要对自动机有一个简单的了解，鉴于篇幅，自动机的内容本文不做介绍。

在查找最优的Value时，会用到求最短路径的Dijikstra算法,但建图过程于此无关。

三，创建FST

为了让大家对FST有一个初步的认识，我们举一个简单的例子来进行说明。

我们假设创建一组映射：Key  →  Value

“cat”  - > 5,

“deep” - > 10，

“do” - > 15

“dog” - > 2,

“dogs” - > 8,

对于经典FST算法来说，要求Key必须按字典序从小到大加入到FST中，原因主要是因为在处理大数据的情况下，我们不太可能把整个FST数据结构都同时放在内存中，而是要边建图边将建好的图存储在外部文件中，以便节省内存。所以我们第一步要对所有的Key排序，对于我给这个例子来说，已经保证了字典序的顺序。

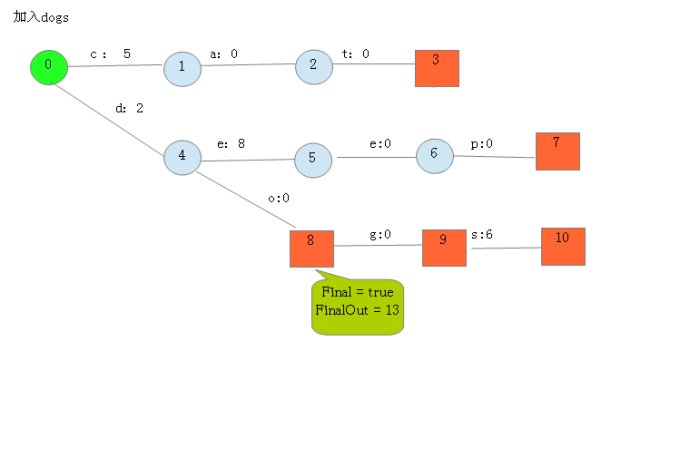
根据此例子的输入我们可以建立下图所示的FST：

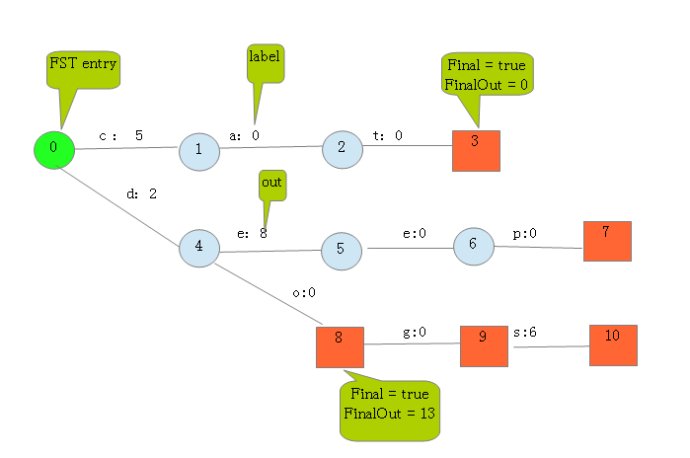
从上图可以看出，每条边有两条属性，一个表示label（key的元素），另一个表示Value(out)。注意Value不一定是数字，还可一是另一个字符串，但要求Value必须满足叠加性，如这里的正整数2 + 8 = 10。字符串的叠加行为： aa + b = aab。

建完这个图之后，我们就可以很容易的查找出任意一个key的Value了。例如：查找dog，我们查找的路径为：0 → 4 → 8 → 9。 其权值和为： 2 + 0 + 0 + 0 = 2。其中最后一个零表示 node[9].finalOut = 0。所以“dog”的Value为2。

到这里，我们已经对FST有了一个感性的认识，下面我们详细讨论FST的建图过程：

1，建一个空节点，表示FST的入口，所有的Key都从这个入口开始。

2，   如果还有未处理的Key，则枚举Key的每一个label。

处理流程如下：

如果当前节点存在含此label的边，则

如果Value包含该边的out值，则

Value = Value – out

否则

令temp=out–Value；

out =Value并使下一个节点的所有边out都加上temp。

如果下一节点是Final节点 则FinalOut += temp

进入下一个节点

否则： 新建一个节点另其out = Value， Value = 0。

如果你看不懂，没关系，我们将用例子演示一遍概算法：

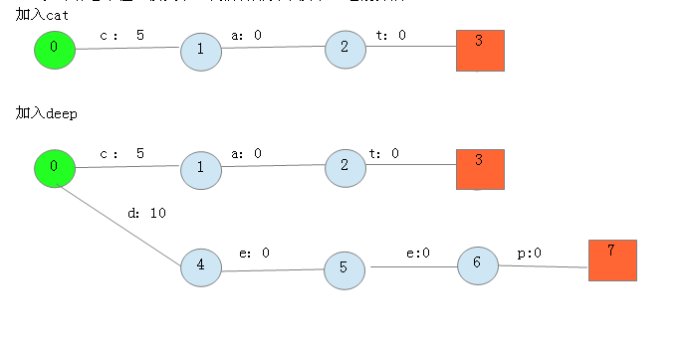
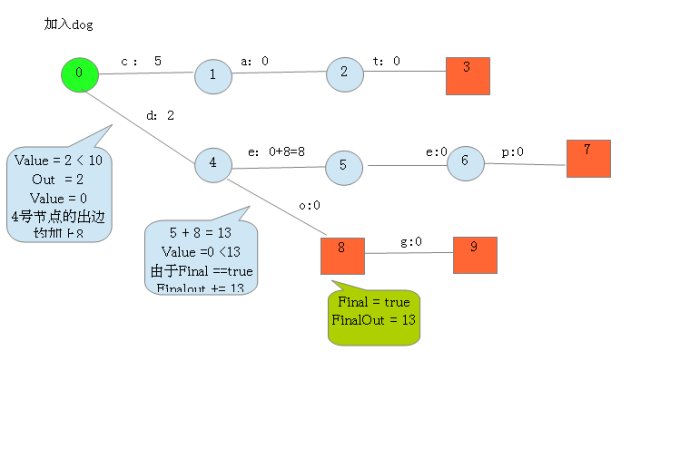
四， 存储FST

通过上面的算法我们看到，FST 本身并不要求输入要按照字典序从小到大，但正如我文章开头说的那样，FST只是一个映射，只能成为我们应用程序的一个工具，所以决不能让这个工具占用我们过多宝贵的内存空间，因此我们要把不用的节点存入到文件中。但是我们的问题是什么样的节点才是不要的节点呢，要解决这个问题还得回顾我们刚才的算法流程。

我们发现存储cat字符串的三个节点自从开始处理deep后就在也没用到过，这是巧合么？如果这是个巧合，那么当开始处理do后就再也没用到过存储eep的三个节点，这是巧合么？如果不是巧合，那到底是什么原因呢？很明显是字典序在做怪！！

正因为，我们保证了所有的Key都是按照字典序加进来的，所以当加入一个新Key的时侯，我们可以先求出新加的Key和上一次输入的Key的公共前缀，然后就可以把 上一次输入的Key除去公共前缀剩下的部分存入文件中了。

综上，可知FST是强大的，但内存是有限的，导致我们必须保证输入有序。

五，应用

尽管FST足够强大，但是在应用过程中，我们仍然可以对其进行再优化，自然语言处理我不太了解，所以不太清楚要如何使用FST来处理自然语言，但是我接触最多的FST的应用就是Lucene。FST在Lucene4.0以后的版本中用于快速定位所查单词在字典中的位置即FST<IntsRef，byteSequence>，由于Lucene是以二进制存储的，所以byteSecquence相当于一个数值，即用多个byte去表示一个数。在Lucene中允许用户设置两个整数minCount1，和minCount2，同时每一个节点记录经过自己的单词数c。

如果c < minCount1 则不存储该节点，因为在大量的文档中，以当前单词为前缀的单词数很少则没有存储的必要，以节省空间。

如果该节点的父节点所经过的单词数pc < minCount2 则删除该节点，原因和上面一样。一般minCount2 >= minCount1。

同时Lucene尽量缩减存储一个节点所需要的空间，比如状态压缩方法。

六，总结

由于网上资料少，自己英语又戳，所以花废了整整一天的时间慢慢啃代码才把此算法弄清楚，鉴于本人时间较紧，所以没有附上自己的程序，如果想了解请查看Lucene4.0官方开源代码Builder.java 的add 方法。目前Lucene还支持FST的反映射，即通过Value找Key，以及前k小的Key（按照Value大小排序）。其实就是在FST上用Dijikstra求最短路。