【noip模拟】tree

Time Limit: 1000 ms        Memory Limit: 128 MB

[吐槽]

　　点分治点分治点分治

　　嗯。。场上思考树状数组的时候好像傻掉了。。反正就是挂了就是了。。

[题解]

　　首先如果没有环的话就是一道十分简单的点分治啦

　　但是这题有环啊

　　

　　考虑强行变树

　　从题目各种谜一般的描述中得出来的结论是：$m<=n$

　　其实也就是说最多只有一个环

　　那么就有一个很直接的想法，先把唯一的一个环找出来，断掉其中的一条边

　　这样就使它变成一棵树了，直接跑一遍点分就好

　　考虑断掉的那条边

　　这样统计有一个很明显的问题：经过断开那条边的情况全部都没有算进去

　　所以现在就考虑怎么算过这条边的ans

　　

　　首先我们可以将这个环摊开变成这样：

　　

　　

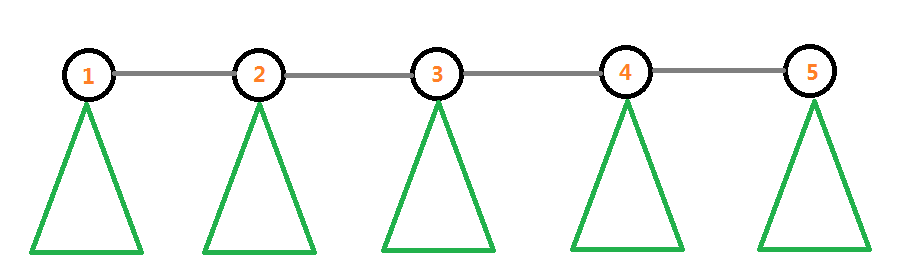
　　然后发现这个东西其实就是一条“链”上面有若干棵树

　　断开的那条边显然就是连接这条“链”一头一尾的边（为了方便描述，将这条断开的边记作$(x,y)$）

　　我们定义

　　$rt_i$表示$i$所属的子树的根节点

　　$dis_i$ 表示$i$到$rt_i$的的路径上的点数

　　$left_i$表示$rt_i$到这条“链”头（也就是图中编号为1的点）的节点数

　　$right_i$表述$rt_i$到这条“链”尾（图中编号为5的点）的节点数

　　那么要算一条过$(x,y)$的路径$(i,j)$的点数的话，显然就是子树里面的距离+链上要走的距离

　　也就是 $dis_i+dis_j+left_i+right_j$ （$rt_i$在$rt_j$左边）

　　

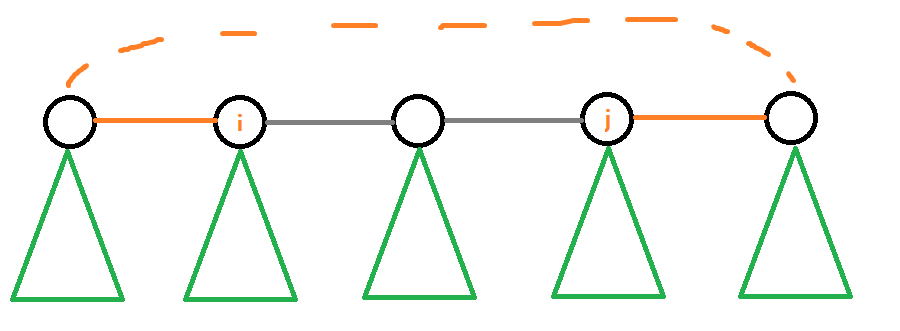
　　那么就可以用一个树状数组来搞定了

　　考虑怎么统计

　　（其实实现起来并不用上面的那些奇妙数组）

　　我们可以先将链上的点（也就是各个子树的根节点）编个号

　　那么对于一个这条链上面的第$i$和第$j$ $(i<j)$ 个点，那么链上要走的距离就为 $i+(len-j+1)$

　　其中$len$表示的是链的长度

　　然后将式子上一步中求路径上点数的式子稍微整理一下，得到

　　$(dis_i+i)+(dis_j+len-j+1)  (i<j) $

　　

　　所以我们可以从左往右一个一个点处理

　　先将当前点$i$子树内的$dis$处理出来

　　然后对于每一个$dis_j (j \in subtree(i))$ ，在树状数组里面查询大于等于$k-dis_j-(len-j+1)$的数量（原因在后面解释）

　　查询完了之后将$dis_j+j$丢入树状数组中

　　这么处理的原因显然

　　整理过后的式子可以分为两部分，分别只与$i$和$j$有关

　　然后因为我们是从左到右处理链上面的点的，所以可以保证查询到的点是在当前点的前面的

　　然后这题就十分愉快地解决啦

[一些小细节]

　　因为这题是求>=的方案数

　　所以树状数组要十分愉快地反过来（也就是insert的时候是x-=x&-x，query的时候是x+=x&-x，见代码）

　　以及因为insert的时候是dis+i，所以上限应该是2*n

　　以及要用long long

　　嗯大概就是这样ovo

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #define ll long long
 using namespace std;
 const int MAXN=;
 int h[MAXN],size[MAXN],mx[MAXN];
 ll dis[MAXN];
 bool vis[MAXN];
 int n,m,k,tot,rt,rt_mx;
 ll ans,num;
 struct xxx
 {
     int y,next;
     bool flag;
 }a[MAXN*];
 struct data
 {
     ll c[MAXN*];
     int insert(int x,ll delta) {_insert(x,delta);}
     int _insert(int x,ll delta)
     {
         for (;x;x-=x&-x) c[x]+=delta;
     }
     ll query(int x) {return _query(x);}
     ll _query(int x)
     {
         ll ret=;
         if (x<) x=;
         for (;x<=*n;x+=x&-x) ret+=c[x];
         return ret;
     }
 }c;
 int pre[MAXN],cir[MAXN];
 int add(int x,int y);
 int dfs(int x);
 int dfs_size(int x,int fa);
 int dfs_root(int r,int x,int fa);
 int get_dis(int x,int fa,int d);
 int get_cir(int fa,int x);
 ll cal(int x,int d);
 bool cmp(int x,int y){return x>y;}
 int solve_cir();

 int main()
 {
     freopen("a.in","r",stdin);
     freopen("a.out","w",stdout);

     int x,y,z;
     scanf("%d%d%d",&n,&m,&k);
     tot=;
     memset(h,-,sizeof(h));
     for (int i=;i<=m;++i)
     {
         scanf("%d%d",&x,&y);
         add(x,y); add(y,x);
     }
     if (m+==n) {dfs(); printf("%lld\n",ans); return ;}
     cir[]=;
     get_cir(,);
     solve_cir();
 }

 int add(int x,int y)
 {
     a[++tot].y=y; a[tot].next=h[x]; h[x]=tot; a[tot].flag=true;
 }

 int dfs(int x)
 {
     rt=,rt_mx=n;
     dfs_size(x,);
     dfs_root(x,x,);
     ans=ans+cal(rt,);
     vis[rt]=true;
     for (int i=h[rt];i!=-;i=a[i].next)
         if (!vis[a[i].y]&&a[i].flag)
         {
             ans=ans-cal(a[i].y,);
             dfs(a[i].y);
         }
 }

 int dfs_size(int x,int fa)
 {
     size[x]=;
     mx[x]=;
     for (int i=h[x];i!=-;i=a[i].next)
         if (a[i].y!=fa&&!vis[a[i].y]&&a[i].flag)
         {
             dfs_size(a[i].y,x);
             size[x]+=size[a[i].y];
             mx[x]=max(mx[x],size[a[i].y]);
         }
 }

 int dfs_root(int r,int x,int fa)
 {
     mx[x]=max(mx[x],size[r]-size[x]);
     if (rt_mx>mx[x]) rt_mx=mx[x],rt=x;
     for (int i=h[x];i!=-;i=a[i].next)
         if (a[i].y!=fa&&!vis[a[i].y]&&a[i].flag)
             dfs_root(r,a[i].y,x);
 }

 int get_dis(int x,int fa,int d)
 {
     dis[++num]=d;
     for (int i=h[x];i!=-;i=a[i].next)
         if (a[i].y!=fa&&!vis[a[i].y]&&a[i].flag)
             get_dis(a[i].y,x,d+);
 }

 ll cal(int x,int d)
 {
     num=;
     get_dis(x,,d);
     int left=,right=num;
     ll re=;
     sort(dis+,dis++num,cmp);
     while (left<right)
     {
         while (dis[left]+dis[right]+<k&&left<right) --right;
         re+=right-left;
         ++left;
     }
     return re;
 }

 int get_cir(int fa,int x)
 {
     int u;
     vis[x]=true; pre[x]=fa;
     for (int i=h[x];i!=-;i=a[i].next)
     {
         u=a[i].y;
         if (u==fa) continue;
         if (vis[u])
         {
             a[i].flag=false; a[i^].flag=false;
             for (int j=x;j!=u;j=pre[j]) cir[++cir[]]=j;
             cir[++cir[]]=u;
             return ;
         }
         get_cir(x,u);
         if (cir[]) return ;
     }
 }

 int solve_cir()
 {
     for (int i=;i<=n;++i) vis[i]=false;
     dfs();
     for (int i=;i<=n;++i) vis[i]=false;
     for (int i=;i<=cir[];++i) vis[cir[i]]=true;
     for (int i=;i<=cir[];++i)
     {
         num=;
         get_dis(cir[i],,);
         for (int j=;j<=num;++j)
             ans+=c.query(k-dis[j]-(cir[]-i+));
         for (int j=;j<=num;++j)
             c.insert(dis[j]+i,);
     }
     printf("%lld\n",ans);
 }

挫挫的代码