js算法初窥04（算法模式01-递归）

　　终于来到了有点意思的地方——递归，在我最开始学习js的时候，基础课程的内容就包括递归，但是当时并不知道递归的真正意义和用处。我只是知道，哦...递归是自身调用自身，递归要记得有一个停止调用的条件。那时，我还不了解递归的内在含义，好在现在知道了一点。

　　有些问题的本身就是递归的，我们想一个程序问题，也是比较经典的面试问题——有一个对象a，我们不知道它有多少层级，如何复制对这个对象?你可能会说，直接声明一个变量var b = a不就可以了嘛？但是，如果我改动了a中的一个属性，b中的属性也跟着改变了。因为你只是将b得到指针指向了a，并没有开辟一块新的空间来存储“存储在a中的属性”。也就是我们所谓的浅拷贝。那么如何改变a中的属性，b的属性还是原来的样子呢？我们可以利用递归来解决这样的问题。

　　我记得前面的文章（用js来实现那些数据结构05（栈02-栈的应用））例举了用栈解决问题的实例。其中最后一个问题是汉诺塔问题，也需要用递归来解决。那么就汉诺塔问题来说，如果不用递归，是否还有其它的可行的算法得以解决这样的问题呢？

　　很多人会觉得递归是低效率的，只不过是因为人脑的有限性不得不让计算机去更忙碌一点，其实这种想法实在是片面的。因为有些问题本身就是递归的，比如我们上面所举例子。再比如，有些问题或许可以递归，可以循环，还可以用其他方法来解决，但是递归更容易让我们的代码简洁易懂，于是我们选择了递归。

　　好了，说了很多，我们还是回到递归本身吧，递归说到底是一种解决问题的方法，它解决问题的各个小部分，直到解决最初的大问题。那么，递归通常都会调用自身，就像下面这样：

function a() {
    a();
}

　　当然，这样写也是一样的：

function a() {
    b();
}
function b() {
    a();
}

　　当然，上面代码只是举个例子，没有什么实际意义。

　　在我们在最开始试着去实现一个递归的时候，往往会出现stack overflow error等类似栈溢出的错误。因为我们的递归无限的执行下去以至于浏览器不得不强制停止递归，然后告诉你，出错了。我们可以写一点简单的代码来测试一下：

var i = 0;
function recursiveFn() {
    i++;
    recursiveFn();
}

try{
    recursiveFn();
} catch(err) {
    console.log(i,"error is:" + err);
}
// Google
//15710 "error is:RangeError: Maximum call stack size exceeded"
// FireFox
//65657 error is:InternalError: too much recursion
//QQ
// 41756 "error is:RangeError: Maximum call stack size exceeded"
//ie
//8225 error is:Error: 堆栈溢出
//edge
// 15466 error is:Error: Out of stack space

　　我们发现似乎每一个浏览器，栈溢出的上限都是不一样的。因为每一种浏览器厂商都为其自己的浏览器设置了不同的限度。甚至包括一些js原生api的内部实现方式，在不同的浏览器上都是不一样的。

　　我们发现递归是如此的简单，就是自身调用自身，再加一个限制条件，就可以实现递归了。上面我们所写的代码在一定程度上只是为了解释递归这个概念。没有太多的实际意义。那么，下面我们看看用递归来解决斐波那契数列问题。

　　那么我们先来看这样一个问题，经典的兔子繁殖问题。一般而言，兔子在出生两个月后，就有繁殖能力，一对兔子每个月能生出一对小兔子来。如果所有兔子都不死，那么一年以后可以繁殖多少对兔子？

我们不妨拿新出生的一对小兔子分析一下：第一个月小兔子没有繁殖能力，所以还是一对，两个月后，生下一对小兔，对数共有两对，三个月以后，老兔子又生下一对，因为小兔子还没有繁殖能力，所以一共是三对。依次类推：

　　

　　这就是斐波那契数列了，在生活中，也有许多斐波那契数列存在的地方。

　　那么我们可以提取一下：1和2的斐波那契数是1，3的斐波那契数是2，4的斐波那契数是3。换句话说，在n>2的情况下，F(n) = F(n-1) + F(n - 2)——这里的n代表着在斐波那契数列中的第几个斐波那契数。那么，我们再用语言描述一下——除开最开始的两项以外，以后的每一项都是前两项的和，这就是我们的递归体和递归终止条件，我们来看下代码：

function fibonacci(num) {
    if(num === 1 || num === 2) {
        return 1;
    }

    return fibonacci(num - 1) + fibonacci(num - 2);
}

console.log(fibonacci(6))

　　要注意，不要试超过50的数噢，因为越往后相加的计算量就会越来越巨大。那么我们画个图来看看，我们递归算出第6项的斐波那契数时，递归是如何进行的：

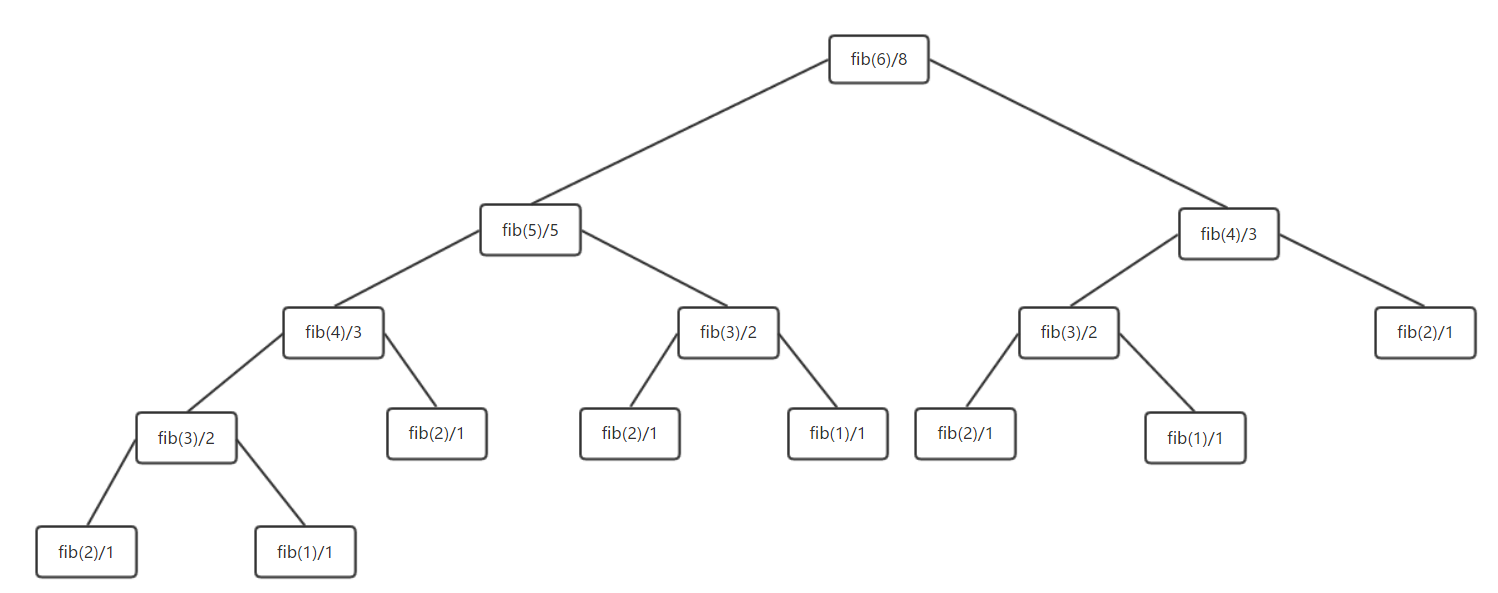
　　我们看上图一步一步的解释：

　　每一个方块中“/”后面的是当前调用的计算结果。我们从第一次fib(6)开始，由于6既不是1也不是2所以停止条件不符合，我们直接return了两次调用但是这两次调用又对num参数做了减一和减二的操作。所以就到了下一层。直到最后每一层的调用都执行到了num=1或者num=2的情况时。递归最终终止。那么，在递归终止的时候，结果是由递归到最底层条件一点一点向上返回的。所以，递归的执行时由上至下但是递归结果的返回则是由下至上的。这样我们就完成了一次整个递归的过程。

　　最后，由于本人水平有限，能力与大神仍相差甚远，若有错误或不明之处，还望大家不吝赐教指正。非常感谢！