[网络流]BZOJ4657 最小割约束

题面：

Description
Nick最近在玩一款很好玩的游戏，游戏规则是这样的：
有一个n*m的地图，地图上的每一个位置要么是空地，要么是炮塔，要么是一些BETA狗，Nick需
要操纵炮塔攻击BETA狗们。
攻击方法是：对于每个炮塔，游戏系统已经给出它可以瞄准的方向(上下左右其中一个），Nick需要
选择它的攻击位置，每一个炮塔只能够攻击一个位置，炮塔只能够向着它的瞄准方向上的某个位置发
动攻击，当然炮塔也可以不进行攻击。炮塔威力强大，它可以且仅可以消灭目标位置上所有的BETA狗。
出于安全考虑，游戏系统已经保证不存在一个炮塔能够瞄准另外一个炮塔，即对于任意一个炮
塔，它所有可能的攻击位置上不存在另外一个炮塔。而且，如果把炮塔的起点和终点称为炮弹的运行
轨迹，那么系统不允许两条轨迹相交（包括起点和终点）。
现在，选定目标位置以后，每一个炮塔同时开炮，你要告诉Nick，他最多可以干掉多少BETA狗。
Input
第一行两个正整数n，m，表示地图的规模。
接下来礼行，每行m个整数，0表示空地，-1，-2，一3，-4分别表示瞄准上下左右的炮塔，若为正整
数p，则表示该位置有p个BETA狗。
n，m <= 50，每个位置的BETA狗数量不超过999个，保证不存在任意一个炮塔能够瞄准另外一个炮塔
Output
一个正整数，表示Nick最多可以干掉几个BETA狗
Sample Input
3 2
0 9
-4 3
0 -1
Sample Output
9
分析：

显然，题目保证了只有横炮台与纵炮台才可能会有相交的攻击轨迹。

然后对于每对有相交攻击范围的横炮台与纵炮台，它们对答案的贡献得分不仅决定于它们自己的攻击范围内的BETA狗，还会被其它的炮台所局限。所以，每个炮台对于进攻目标的选择，正好需要最大流最小割的类似自我调整的性质。

考虑如何连边。如果从最大流的角度思考，难以表达“炮台A选了BEAT狗a，炮台B就不能选a”这种逻辑关系，所以改换最小割。若一对纵横炮台A与B存在公共轨道，可以看成A到B有一条路径，就像这样：

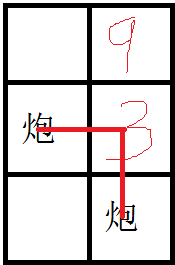
那么我们割就是让两个炮台无法相交。

如果两个炮台要攻击最大值时都要去跨过它们攻击轨道的相交点，那么我们的割就要让其中一个炮台无法越过相交点，另一个不再受那个炮台的约束。

我们可以把所有点拿出来当一个部，每个炮台的轨道上的点依次连边。

若该轨道为纵向，则轨道上的第一个点与原点连边，方向与炮台方向相同，同理连第一个点与第二个点，方向与炮台相同（因为打到一个点时，它之前的点会被轨道覆盖，所以不能分别与原点连边），以此类推。若该轨道为横向，则第一个点与汇点连边，方向与炮台方向相反，以此类推。

又因为两个炮台之间的路径只能有一次拐弯，故拆点，左边的点表示纵向轨迹，右边的点表示横向轨迹，相同的点之间从左到右连一条边。

这样就可以表示出全部的纵炮到横炮的路径（纵横可以反过来）。

接下来考虑一下割边的代价。

我们先来考虑割边的意义。割某条边就代表有一个炮台打到的点只能是那个边的一个端点，而另外一个的炮台就不再受这个炮台的限制。

所以，首先满足的是割的边必须是同一条轨道上相邻点之间的边，所以 相同点之间的边 和 点与汇点,源点的边 的代价（即容量）为inf。这样它们就不会被割了。

对于其它边的讨论，容我摘一段xmy大佬的解释：

把炮塔能够打到的beta狗中的最大值记为mx，那么炮塔路径最多只会延伸到第一个mx，再往后只会更劣。我们先把每个炮塔的mx加入ans中。

对于竖炮塔的一条边u->v，割掉它表示炮塔打到了u点，那么ans就会损失掉mx-u点的beta狗的值，于是这条边的容量为mx-u点的beta狗。

对于横炮塔的一条边u->v，割掉它表示炮塔打到了v点，那么ans就会损失掉mx-v点的beta狗的值，于是这条边的容量为mx-v点的beta狗。

所以答案就是ans-最小割。

最后附上代码

#include<cstdio>
#include<cstring>
#include<algorithm>
#define p(i,j) (i-1)*m+j
using namespace std;
const int maxp=,inf=0x3f3f3f3f;
int n,m,tot,map[][], dx[]={-,,,},dy[]={,,-,},d[maxp],vd[maxp];
int S,T,ans,cnt=,sum,info[maxp];
struct flow{int u,v,nex,w;}e[];
int sap(int i,int augco)
{
    if(i==T)return augco;
    int j,tmp,ret=,mind=T-;
    for(int o=info[i];o;o=e[o].nex)
    {
        j=e[o].v;
        if(e[o].w>){
            if(d[i]==d[j]+)
            {
                tmp=sap(j,min(e[o].w,augco));
                e[o].w-=tmp;
                e[o^].w+=tmp;
                ret+=tmp;
                augco-=tmp;
                if(d[]>=T)return ret;
                if(augco==)break;
            }
            mind=min(mind,d[j]);
        }
    }
    if(ret==)
    {
        vd[d[i]]--;
        if(vd[d[i]]==)
            d[]=T;
        d[i]=mind+;
        vd[d[i]]++;
    }
    return ret;
}
void solve()
{
    memset(vd,,sizeof vd);
    memset(d,,sizeof d);
    vd[]=T;ans=;
    while(d[S]<T)
        ans+=sap(,inf);
}
void add(int u,int v,int w)
{
    //printf("%d %d %d\n",u,v,w);
    e[++cnt]=(flow){u,v,info[u],w};info[u]=cnt;
    e[++cnt]=(flow){v,u,info[v],};info[v]=cnt;
}
int main()
{
    scanf("%d%d",&n,&m);S=;T=+n*m+n*m+;
    for(int i=;i<=n;i++)for(int j=;j<=m;j++)scanf("%d",&map[i][j]);
    for(int i=;i<=n;i++)for(int j=;j<=m;j++)if(map[i][j]<)
    {
        int k=-map[i][j]-,mx=,x,y;
        map[i][j]=;
        for(x=i+dx[k],y=j+dy[k];<=x&&x<=n&&<=y&&y<=m;x+=dx[k],y+=dy[k])mx=max(mx,map[x][y]);
        sum+=mx;
        if(k==||k==)
        {
            add(S,+p(i,j),inf);
            for(x=i,y=j;map[x][y]!=mx;x+=dx[k],y+=dy[k])
                add(+p(x,y),+p(x+dx[k],y+dy[k]),mx-map[x][y]);
        }
        if(k==||k==)
        {
            add(+n*m+p(i,j),T,inf);
            for(x=i,y=j;map[x][y]!=mx;x+=dx[k],y+=dy[k])
                add(+n*m+p(x+dx[k],y+dy[k]),+n*m+p(x,y),mx-map[x][y]);
        }
    }
    for(int i=;i<=n*m;i++) add(+i,+n*m+i,inf);solve();
    printf("%d\n",sum-ans);
}