计蒜客NOIP模拟赛6 D1T1Diamond-square

Diamond-square 算法是一种能够用于生成噪声的算法，现在我们考虑这个算法的一个变种。

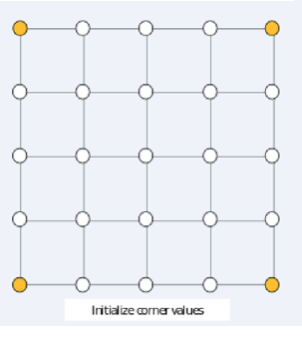
你有一个 2^n\times 2^n2​n​​×2​n​​ 的网格，一共有 (2^n+1)^2(2​n​​+1)​2​​个格点，现在给定四个角的初始权值以及一个值 xx。

整个算法由若干个 diamond step 和 square setp 交替进行来构成。

在一个 diamond step 或者 square step 中，会有若干个之前没有被赋值的点被赋值，其值等于之前的某四个或三个点的值的和加上 xx。

xx 的值每进行完一次 diamond step 和一次 square step 之后就会变成原来的二倍。

而具体的过程用图来描述如下，在样例解释中可以看到更详细的文字解释：

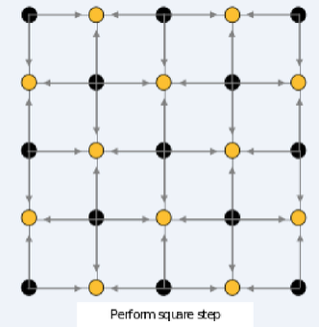
现在我们想知道整个矩阵最后的值的和模 10^9+710​9​​+7 等于多少。

输入格式

一行 66 个整数，分别代表 nn，左上角权值，右上角权值，左下角权值，右下角权值，xx 的初始值。

保证初始权值和 xx 都在 [0,10^9+7)[0,10​9​​+7)之内。

输出格式

一行一个整数，代表矩阵内所有元素的和模 10^9+710​9​​+7 的值。

数据规模

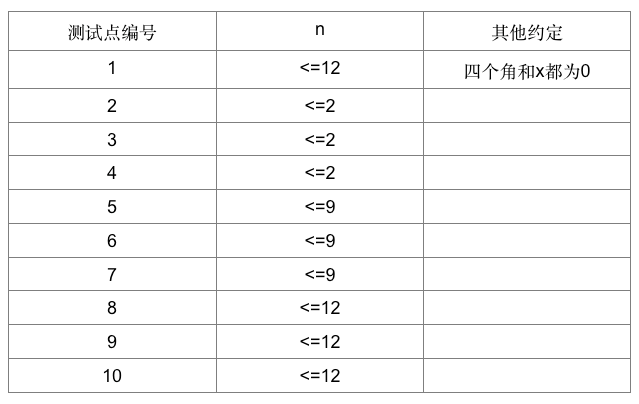
样例解释

最终矩阵如下：

 

 

 

 

 

1

0    446   112   590   24    590   112   446   0

2

456  326   976   446   1142  446   976   326   456

3

122  1046  84    1346  218   1346  84    1046  122

4

670  506   1446  590   1428  590   1446  506   670

5

34   1382  258   1578  22    1578  258   1382  34

6

780  576   1656  700   1728  700   1656  576   780

7

162  1326  114   1756  298   1756  114   1326  162

8

646  466   1396  636   1622  636   1396  466   646

9

10   656   172   860   44    860   172   656   10

 

 

如题面图，四个角赋为初始值，随后开始执行算法：

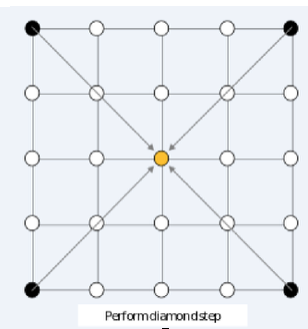
Diamond step：中点被赋值为四个角的和 +x+x。

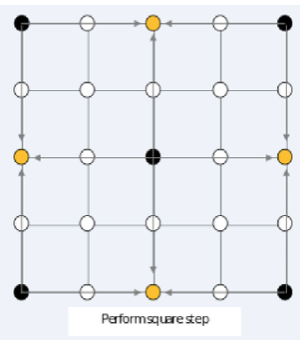
Square step：四条边的中点被赋值为所在边的两个端点与中点的和 +x+x。

xx 变为原来的两倍。

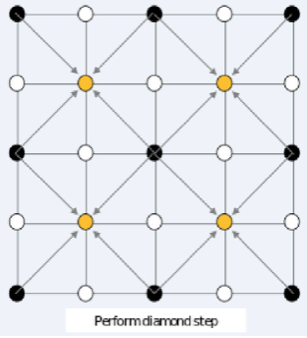
Diamond step：把整个矩阵分成四个等大小的正方形，这四个正方形的中点被分别赋值为正方形的四角的和 +x+x。

Square step：把整个矩阵分成四个大小相等的正方形，对于每个正方形的每一条边的中点，把他赋值为其向上下左右四个方向找到的第一个已经被赋值的点的和 +x+x（对于整个矩形的边界上的点，会有一个方向不存在，那么这个点被赋值为另外三个方向的和 +x+x）。

xx 变为原来的两倍。

所有点都被赋值，算法结束。

忽略每行输出的末尾多余空格

样例输入

3 0 0 10 10 2

样例输出

55178
不多BB，直接模拟就行了O(4n)
要注意尽可能少枚举多余的状态，如果变成了O(n*4n)就会超时

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 typedef long long lol;
 lol Mod=;
 lol pw[],a[][],d,n,ans;
 int main()
 {int i,j,flag,k;
     cin>>n;
     pw[]=;
     for (i=;i<=n;i++)
     pw[i]=pw[i-]*;
     cin>>a[][]>>a[][pw[n]]>>a[pw[n]][]>>a[pw[n]][pw[n]]>>d;
     for (i=n;i>=;i--,(d*=)%=Mod)
     {
         for (j=;j<pw[n];j+=pw[i])
         {
             for (k=;k<pw[n];k+=pw[i])
             {
                 int x=j+pw[i-],y=k+pw[i-];
                 a[x][y]=a[j][k]+a[j+pw[i]][k]+a[j][k+pw[i]]+a[j+pw[i]][k+pw[i]]+d;
             a[x][y]%=Mod;
             }
         }
         flag=;
         for (j=;j<=pw[n];j+=pw[i-],flag^=)
         {
             for (k=flag*pw[i-];k<=pw[n];k+=pw[i])
             {
                 if (j-pw[i-]>=)
                 a[j][k]+=a[j-pw[i-]][k];
                 if (j+pw[i-]<=pw[n])
                 a[j][k]+=a[j+pw[i-]][k];
                 if (k-pw[i-]>=)
                 a[j][k]+=a[j][k-pw[i-]];
                 if (k+pw[i-]<=pw[n])
                 a[j][k]+=a[j][k+pw[i-]];
                 a[j][k]+=d;
                 a[j][k]%=Mod;
             }
         }
     }
     for (i=;i<=pw[n];i++)
     for (j=;j<=pw[n];j++)
     ans+=a[i][j],ans%=Mod;
     cout<<ans;
 }