BZOJ_2595_[Wc2008]游览计划_斯坦纳树

BZOJ_2595_[Wc2008]游览计划_斯坦纳树

题意：

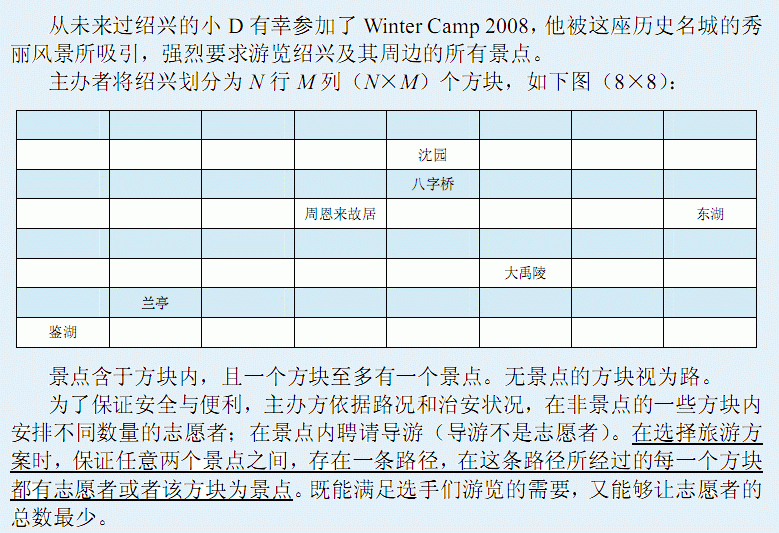
分析：

斯坦纳树裸题，有几个需要注意的地方

给出矩阵，不用自己建图，但枚举子集转移时会算两遍，需要减去当前点的权值

方案记录比较麻烦，两边的转移都需要记录，最后dfs找方案会比较容易理解

代码：

#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <queue>
using namespace std;
#define N 110
#define LL long long
priority_queue <pair <int,int> >q;
LL map[11][11],dis[1<<10][N];
int chosex[1<<10][N],chosey[1<<10][N];
bool change[1<<10][N];
int flg[11][11];
int n,m;
int tx[]={1,-1,0,0};
int ty[]={0,0,1,-1};
int id[N][N],a[N],xx[N],yy[N],cnt,vis[1<<10][N];
void dfs(int sta,int p){
    if(!dis[sta][p])return ;
    flg[xx[p]][yy[p]]=1;
    if(change[sta][p]){
        dfs(chosex[sta][p],p);
        dfs(chosey[sta][p],p);
    }else dfs(sta,id[chosex[sta][p]][chosey[sta][p]]);
}
int main(){
    scanf("%d%d",&n,&m);
    int i,j,tot=0,k,x;
    for(i=1;i<=n;i++){
        for(j=1;j<=m;j++){
            scanf("%lld",&map[i][j]);
            id[i][j]=++tot;
            xx[tot]=i;yy[tot]=j;
            if(!map[i][j]){
                a[++cnt]=tot;
            }
        }
    }
    int mask=(1<<cnt)-1;
    memset(dis,0x3f,sizeof(dis));
    for(i=1;i<=cnt;i++){
        dis[1<<i-1][a[i]]=0;
    }
    for(j=1;j<=mask;j++){
        for(i=1;i<=n*m;i++){
            for(k=j&(j-1);k;k=j&(k-1)){
                if(dis[j][i]>dis[k][i]+dis[j-k][i]-map[xx[i]][yy[i]]){
                    dis[j][i]=dis[k][i]+dis[j-k][i]-map[xx[i]][yy[i]];
                    chosex[j][i]=k,chosey[j][i]=j-k;
                    change[j][i]=1;
                }
                // dis[j][i]=min(dis[j][i],dis[k][i]+dis[j-k][i]-map[xx[i]][yy[i]]);
            }
        }
        for(i=1;i<=n*m;i++){
            q.push(make_pair(-dis[j][i],i));
        }
        while(!q.empty()){
            x=q.top().second;q.pop();
            if(vis[j][x])continue;
            vis[j][x]=1;
            int nx=xx[x],ny=yy[x];
            for(i=0;i<4;i++){
                int dx=nx+tx[i],dy=ny+ty[i];
                if(dx>=1&&dx<=n&&dy>=1&&dy<=m){
                    if(dis[j][id[dx][dy]]>dis[j][x]+map[dx][dy]){
                        dis[j][id[dx][dy]]=dis[j][x]+map[dx][dy];
                        chosex[j][id[dx][dy]]=nx;
                        chosey[j][id[dx][dy]]=ny;
                        change[j][id[dx][dy]]=0;
                        q.push(make_pair(-dis[j][id[dx][dy]],id[dx][dy]));
                    }
                }
            }
        }
    }
    LL ans=1ll<<60;
    int end;
    for(i=1;i<=n*m;i++){
        if(ans>dis[mask][i]){
            ans=dis[mask][i];
            end=i;
        }
        // ans=min(ans,dis[mask][i]);
    }
    dfs(mask,end);
    printf("%lld\n",ans);
    for(i=1;i<=n;i++){
        for(j=1;j<=m;j++){
            if(!map[i][j]){
                printf("x");
            }else if(flg[i][j]){
                printf("o");
            }else printf("_");
        }
        puts("");
    }
}