SP839 Optimal marks（最小割）

SP839 Optimal marks（最小割）

给你一个无向图G（V，E）。 每个顶点都有一个int范围内的整数的标记。 不同的顶点可能有相同的标记。对于边（u，v），我们定义Cost（u，v）= mark [u] \(\oplus\) mark [v]。现在我们知道某些节点的标记了。你需要确定其他节点的标记，以使边的总成本尽可能小。(0 < N <= 500, 0 <= M <= 3000)

先来看一下异或的性质，由于每一位是独立的，我们可以把每一位拉出来分开考虑，变成32个子问题。

现在问题就变成了：一堆点是0，一堆点是1，一堆点没有标号，它们互相有一些边，一个边的权值只当一个点是0一个点是1时才是1，否则是0。求最小边权和

于是我们这样建图：（红色表示1，蓝色表示0，白色表示没有权值）

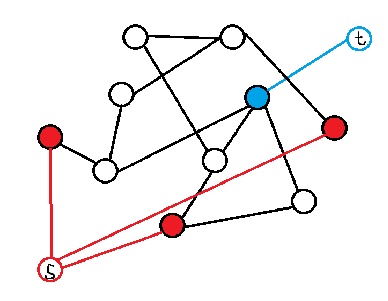
然后跑一个最小割即可。脑补一下，就是找出红色点势力和蓝色点势力的接触处的最小边数。

关于最小割建模的题，具体怎么操作，首先是定义割的含义，就是和s相连的点都定义成要选择的点，其它的点都不选择。关于边的值的定义，不能割的边设置成INF。这个算是套路。

由于题目要求点权和最小，因此我们应尽量让红色点最少。于是，跑完最大流以后，把从s能遍历到的点都标成1就可以满足红色点最少啦！（这个不会证，留坑。）

#include <cstdio>
#include <cstring>
using namespace std;
const int maxn=505, maxm=3005, INF=1e9;
int T, n, m, k, src, dst;
inline int min(int x, int y){ return x<y?x:y; } 
struct Edge{
    int to, nxt, f;
}e[maxm*2+maxn], e1[maxm];
int fir[maxn], cnte;
void addedge(int x, int y, int v){
    Edge &ed=e[++cnte];
    ed.to=y; ed.nxt=fir[x]; ed.f=v; fir[x]=cnte; }
void RESET(){ cnte=1; memset(fir, 0, sizeof(fir)); }
int mark[maxn], gmark[maxn];
int dep[maxn], q[maxn], head, tail;
int bfs(){  //bfs来给图分层
    head=tail=0; memset(dep, 0, sizeof(dep));
    dep[src]=1; q[tail++]=src; int tmp;
    while (head<tail){
        tmp=q[head++];
        for (int i=fir[tmp]; i>0; i=e[i].nxt)
            if (e[i].f>0&&!dep[e[i].to]){
                dep[e[i].to]=dep[tmp]+1;
                q[tail++]=e[i].to;
            }
    }
    return dep[dst]?1:0;
}
int cur[maxn];
int dfs(int u, int flow){  //flow表示从s流到当前点的最大流量 找出一条流
    if (u==dst) return flow;
    if (cur[u]==-1) return 0;
    for (int i=(cur[u]?cur[u]:fir[u]); i>0; i=e[i].nxt){
        cur[u]=i;
        if (dep[e[i].to]==dep[u]+1&&e[i].f){
            int minm=dfs(e[i].to, min(flow, e[i].f));
            if (minm>0){
                e[i].f-=minm; e[i^1].f+=minm;
                return minm;
            }
        }
    }
    cur[u]=-1;
    return 0;
}
void dinic(){
    while (bfs()){
        memset(cur, 0, sizeof(cur));
        while (dfs(src, INF));
	}
}
bool vis[maxn];
void findzero(int u){
	vis[u]=true;
    for (int i=fir[u]; i; i=e[i].nxt){
        if (vis[e[i].to]||!e[i].f) continue;
        findzero(e[i].to);
    }
}
int uu[maxm], vv[maxm];
int main(){
    scanf("%d", &T); int t;
    while (T--){
        scanf("%d%d", &n, &m); dst=n+1;
        for (int i=0; i<m; ++i)
            scanf("%d%d", &uu[i], &vv[i]);
        scanf("%d", &k);
        memset(mark, 0, sizeof(mark));
        memset(gmark, 0, sizeof(gmark));
        for (int i=1; i<=k; ++i){
			scanf("%d", &t); gmark[t]=1;
			scanf("%d", &mark[t]);
		}
        for (int i=0; i<31; ++i){
        	RESET();
        	for (int j=0; j<m; ++j)
        		addedge(uu[j], vv[j], 1), addedge(vv[j], uu[j], 1);
            for (int j=1; j<=n; ++j){
            	if (!gmark[j]) continue;
                if (mark[j]&(1<<i)) addedge(src, j, INF);
                else addedge(j, dst, INF);
            }
            dinic();
            memset(vis, 0, sizeof(vis)); findzero(src);
            for (int j=1; j<=n; ++j)
                if (vis[j]) mark[j]|=(1<<i);
        }
        for (int i=1; i<=n; ++i) printf("%d\n", mark[i]);
    }
    return 0;
}