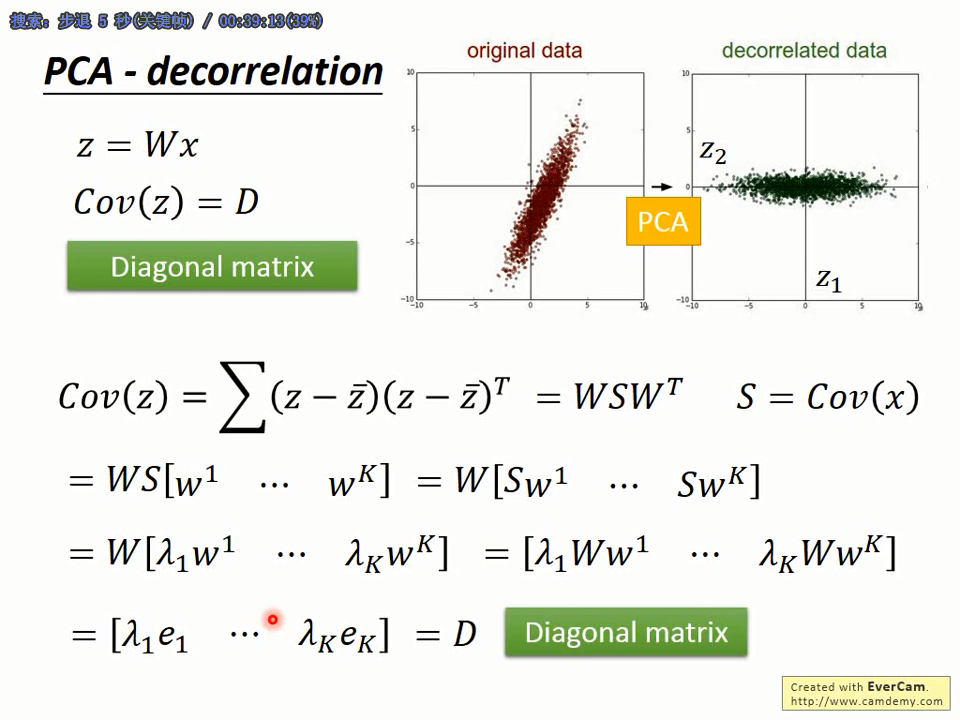
KL变换和PCA的数学推导
一些推导的笔记

上面分解成无穷维,大多数时候都不是的吧。。。

这里的d有限维,应该是指相对小于上面的分解的维度的某个数







参考资料,上面是从最小化损失的角度,利用拉格朗日对偶的优化方法求解
KL变换和PCA的数学推导的更多相关文章
- 主成分分析(PCA)算法,K-L变换 角度
主成分分析(PCA)是多元统计分析中用来分析数据的一种方法,它是用一种较少数 量的特征对样本进行描述以达到降低特征空间维数的方法,它的本质实际上是K-L变换.PCA方法最著名的应用应该是在人脸识别中特 ...
- K-L变换和 主成分分析PCA
一.K-L变换 说PCA的话,必须先介绍一下K-L变换了. K-L变换是Karhunen-Loeve变换的简称,是一种特殊的正交变换.它是建立在统计特性基础上的一种变换,有的文献也称其为霍特林(Hot ...
- PCA的数学原理
PCA(Principal Component Analysis)是一种常用的数据分析方法.PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维 数据的 ...
- PCA的数学原理(转)
PCA(Principal Component Analysis)是一种常用的数据分析方法.PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维数据的降 ...
- Maths | 离散K-L变换/ 主成分分析法
目录 1. 概述 2. K-L变换方法和原理推导 2.1. 向量分解 2.2. 向量估计及其误差 2.3. 寻找最小误差对应的正交向量系 3. K-L变换高效率的本质 4. PCA在编.解码应用上的进 ...
- UVA - 10014 - Simple calculations (经典的数学推导题!!)
UVA - 10014 Simple calculations Time Limit: 3000MS Memory Limit: Unknown 64bit IO Format: %lld & ...
- 统计知识选讲(二)——主成分分析(PCA)的推导和应用
1.数学推导 根据上讲的思想,我们可以用下图来进行数学上的推导. 2.PCA的步骤 1)对原始数据进行标准化处理:对该指标变量进行标准化, 2)计算相关系数矩阵(协方差矩阵) 3)计算相关系数矩阵的特 ...
- LDA-线性判别分析(二)Two-classes 情形的数学推导
本来是要调研 Latent Dirichlet Allocation 的那个 LDA 的, 没想到查到很多关于 Linear Discriminant Analysis 这个 LDA 的资料.初步看了 ...
- 借One-Class-SVM回顾SMO在SVM中的数学推导--记录毕业论文5
上篇记录了一些决策树算法,这篇是借OC-SVM填回SMO在SVM中的数学推导这个坑. 参考文献: http://research.microsoft.com/pubs/69644/tr-98-14.p ...
随机推荐
- Combination Sum I&&II(经典的回溯算法题)
I: Given a set of candidate numbers (C) and a target number (T), find all unique combinations in C w ...
- opencv c++基本操作
常用操作 imread imread (char *filename, int flag=1); 第二个参数,int类型的flags,为载入标识,它指定一个加载图像的颜色类型.可以看到它自带缺省值1. ...
- AC日记——背单词 洛谷 P2353
背单词 思路: KMP+统计前缀和优化: 代码: #include <bits/stdc++.h> using namespace std; #define maxn 1000005 ], ...
- node修改全局环境路径 与 全局后出现sh:exe command not found
修改全局环境路径 当安装nodeJs时候需要修改全局环境的指向,先看看npm config get prefix 全局环境在哪里 然后执行更换命令,一个是主文件一个是缓存文件 npm config ...
- LoadRunner 执行单句SQL语句
LoadRunner 执行单句SQL语句 Action() { int NumRows=0; int i=1; //建立数据库连接 lr_db_connect("StepName=Datab ...
- maven创建springboot项目
1.new Project 2.选择spring Initializr 3.选择next,可以自定义group.artifact,type里可以选择maven也可以选择gradle 4.选择sprin ...
- [解决] python WindowsError: [Error 3]
python 运行出错 WindowsError: [Error ] : 'D:\\\xe7\x81\xab\xe8\xbd\xa6\xe9\x87\x87\xe9\x9b\x86\xe5\x99\x ...
- 洛谷 P3384 【模板】树链剖分-树链剖分(点权)(路径节点更新、路径求和、子树节点更新、子树求和)模板-备注结合一下以前写的题目,懒得写很详细的注释
P3384 [模板]树链剖分 题目描述 如题,已知一棵包含N个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作: 操作1: 格式: 1 x y z 表示将树从x到y结点最短路径上所有节 ...
- 定位所用的class
方案 为解决类冲突,我们可以使用下述的方案定位一个class所在的位置 ClassName. package cn.j2se.junit.classpath; import static org.ju ...
- shell 文件个数 vs 文件夹个数
文件个数 ls -l |grep "^-"|wc -l 文件夹个数 ls -l |grep "^d"|wc -l
