k 近邻算法(k-Nearest Neighbor，简称kNN)

预约助教问题：

1.计算1-NN，k-nn和linear regression这三个算法训练和查询的时间复杂度和空间复杂度?

一、 WHy

最简单最初级的分类器是将全部的训练数据所对应的类别都记录下来，当测试对象的属性和某个训练对象的属性完全匹配时，便可以对其进行分类。但是怎么可能所有测试对象都会找到与之完全匹配的训练对象呢，其次就是存在一个测试对象同时与多个训练对象匹配，导致一个训练对象被分到了多个类的问题，基于这些问题呢，就产生了KNN。

KNN基于这样一种假设，即相似的实例在某种距离度量上应该更为接近。因此在对新实例进行分类时，新实例的分类取决于与其最接近的K个已知实例中出现次数最多的分类(mode)；在对新实例进行回归时，则可使用最接近的K个已知实例的值的平均数。

二、 What

2.1 定义

KNN是通过测量不同特征值之间的距离进行分类。它的的思路是：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。K通常是不大于20的整数。KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

K最近邻(K-Nearest Neighbors, KNN)是一种基于实例的学习方法(instance-based learning)，通过与已有实例的比较来对新的实例进行分类(classification)或回归(regression)。因为基于实例的学习方法在对新实例进行预测之前不需要进行训练，所以也是一种惰性学习方法(lazy learning)。

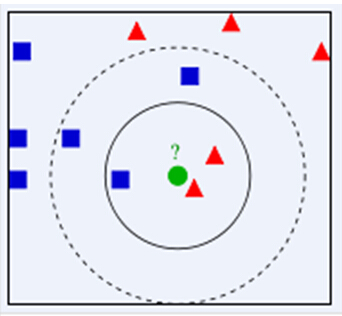
下面通过一个简单的例子说明一下：如下图，绿色圆要被决定赋予哪个类，是红色三角形还是蓝色四方形？如果K=3，由于红色三角形所占比例为2/3，绿色圆将被赋予红色三角形那个类，如果K=5，由于蓝色四方形比例为3/5，因此绿色圆被赋予蓝色四方形类。

2.2 距离函数选择

\[Manhattan Distance (曼哈顿距离) : d(x,y) = \sqrt{ \sum_{k=1}^{n} (x_k - y_k)^2 }
\]

\[Euclidian Distance (欧氏距离) : d(x,y) = \sqrt{ \sum_{k=1}^{n} |x_k - y_k|}
\]

P.S.加权距离——处理维度灾难的一种方法

2.3 Classification vs. Regression

Classification ——— Vote

Regression     ——— Mean

通常，在分类任务中可使用"投票法" 即选择这k 个样本中出现最多的类别标记作为预测结果;

在回归任务中时使用"平均法" ，即将这k 个样本的实值输出标记的平均值作为预测结果.

2.4 优点

无需训练，只需将已知实例存储起来

实现相对简单，例如计算实例之间的距离就比其他动辄需要求解最优化问题的算法要简单得多

2.5 缺点

因为需要将已知实例存储起来，所以需要占用的空间直接取决于实例的数量。

例如在项目中作为成果物提交的分类器，如果是其它方法只需提交训练得到的模型和参数，而基于实例的方法就需要把所有的实例数据都打包，因为其数据即模型。

因为预测时需要与所有已知实例比对，所以耗时也取决于实例的数量。可以用诸如对距离进行排序再进行二分查找的方式优化（此时时间复杂度为\(log_2 N\))

2.6 维度灾难(curse of dimensionality)

    As the number of features or dimensions grows,

    the amount of data we need to generalize accurately also grows exponetially!

    指数增长在CS领域很糟糕！

随着维度的增加，需要维持准确预测的已知实例的数量会随之指数级增加。

因为在增加了新维度之后，已知实例在新空间的投影就变得更稀疏，从而需要比原空间中多得多的实例进行填充

补充：由于KNN训练的代价小(因为不作训练)，KNN或可被用于在线学习(online machine learning)中，即使用新数据不断训练和更新已有模型从而作出更好的预测.

三、How

3.1 pseudocode 伪代码流程

接下来对KNN算法的思想总结一下：就是在训练集中数据和标签已知的情况下，输入测试数据，将测试数据的特征与训练集中对应的特征进行相互比较，找到训练集中与之最为相似的前K个数据，则该测试数据对应的类别就是K个数据中出现次数最多的那个分类，其算法的描述为：

1）计算测试数据与各个训练数据之间的距离；

2）按照距离的递增关系进行排序；

3）选取距离最小的K个点；

4）确定前K个点所在类别的出现频率；

5）返回前K个点中出现频率最高的类别作为测试数据的预测分类。

3.2 Python 代码实例



#coding:utf-8

import numpy #科学计算包

import operator #运算符模块

##给出训练数据以及对应的类别

def createDataSet():

    group = array([[1.0,2.0],[1.2,0.1],[0.1,1.4],[0.3,3.5]])

    labels = ['A','A','B','B']

    return group,labels

###通过KNN进行分类

def classify(input,dataSet,label,k):

    dataSize = dataSet.shape[0] #求数组的行数

    ####计算欧式距离

    diff = tile(input,(dataSize,1)) - dataSet

    #tile使input变为和dataSet相同行数的数组

    #>>> numpy.tile([1.1,0.3],(4,1))#在行方向上重复4次 在列方向上重复1次，

    # array([[ 1.1,  0.3],

#           [ 1.1,  0.3],

#           [ 1.1,  0.3],

#           [ 1.1,  0.3]])

    sqdiff = diff ** 2 # x^2 , y^2

    squareDist = sum(sqdiff,axis = 1) ###矩阵行向量分别相加，从而得到新的一个行向量

#c = np.array([[0, 2, 1], [3, 5, 6], [0, 1, 1]])

#print c.sum()

#print c.sum(axis=0)

#print c.sum(axis=1)

#19

#[3 8 8]

#[ 3 14  2]

    dist = squareDist ** 0.5 # 开根号

    ##对距离进行排序

    sortedDistIndex = argsort(dist)##argsort()根据元素的值从小到大对元素进行排序，返回下标

        ###对选取的K个样本所属的类别个数进行统计

    classCount={}  # 保存A,B出现次数的字典

    for i in range(k):

        voteLabel = label[sortedDistIndex[i]]

        # 获取索引值对应的是A还是B

         # 在字典中保存A,B出现的次数

        classCount[voteLabel] = classCount.get(voteLabel,0) + 1

    ###选取出现的类别次数最多的类别

    maxCount = 0

    for key,value in classCount.items():

        if value > maxCount:

            maxCount = value

            classes = key

    return classes

dataSet,labels = createDataSet()

input = array([1.1,0.3])

K = 3

output = classify(input,dataSet,labels,K)

print("test data :",input,"classification result:",output)

<<<

('test data :', array([ 1.1,  0.3]), 'classification result:', 'A')

参考文章：

http://www.cnblogs.com/littlepear/p/8269653.html

http://www.cnblogs.com/ybjourney/p/4702562.html

http://blog.csdn.net/jmydream/article/details/8644004