Tree - Rooted Trees

Rooted Trees

A graph G = (V, E) is a data structure where V is a finite set of vertices and E is a binary relation on Vrepresented by a set of edges. Fig. 1 illustrates an example of a graph (or graphs).

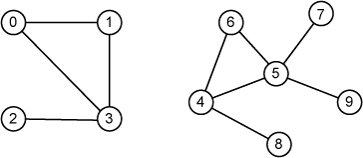
Fig. 1

A free tree is a connnected, acyclic, undirected graph. A rooted tree is a free tree in which one of the vertices is distinguished from the others. A vertex of a rooted tree is called "node."

Your task is to write a program which reports the following information for each node u of a given rooted tree T:

• node ID of u
• parent of u
• depth of u
• node type (root, internal node or leaf)
• a list of chidlren of u

If the last edge on the path from the root r of a tree T to a node x is (p, x), then p is the parent of x, and xis a child of p. The root is the only node in T with no parent.

A node with no children is an external node or leaf. A nonleaf node is an internal node

The number of children of a node x in a rooted tree T is called the degree of x.

The length of the path from the root r to a node x is the depth of x in T.

Here, the given tree consists of n nodes and evey node has a unique ID from 0 to n-1.

Fig. 2 shows an example of rooted trees where ID of each node is indicated by a number in a circle (node). The example corresponds to the first sample input.

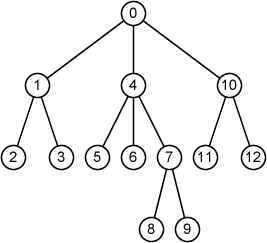
Fig. 2

Input

The first line of the input includes an integer n, the number of nodes of the tree.

In the next n lines, the information of each node u is given in the following format:

id k c1 c2 ... ck

where id is the node ID of u, k is the degree of u, c1 ... ck are node IDs of 1st, ... kth child of u. If the node does not have a child, the k is 0.

Output

Print the information of each node in the following format ordered by IDs:

node id: parent = p , depth = d, type, [c1...ck]

p is ID of its parent. If the node does not have a parent, print -1.

d is depth of the node.

type is a type of nodes represented by a string (root, internal node or leaf). If the root can be considered as a leaf or an internal node, print root.

c1...ck is the list of children as a ordered tree.

Please follow the format presented in a sample output below.

Constraints

• 1 ≤ n ≤ 100000

Sample Input 1

13
0 3 1 4 10
1 2 2 3
2 0
3 0
4 3 5 6 7
5 0
6 0
7 2 8 9
8 0
9 0
10 2 11 12
11 0
12 0

Sample Output 1

node 0: parent = -1, depth = 0, root, [1, 4, 10]
node 1: parent = 0, depth = 1, internal node, [2, 3]
node 2: parent = 1, depth = 2, leaf, []
node 3: parent = 1, depth = 2, leaf, []
node 4: parent = 0, depth = 1, internal node, [5, 6, 7]
node 5: parent = 4, depth = 2, leaf, []
node 6: parent = 4, depth = 2, leaf, []
node 7: parent = 4, depth = 2, internal node, [8, 9]
node 8: parent = 7, depth = 3, leaf, []
node 9: parent = 7, depth = 3, leaf, []
node 10: parent = 0, depth = 1, internal node, [11, 12]
node 11: parent = 10, depth = 2, leaf, []
node 12: parent = 10, depth = 2, leaf, []

Sample Input 2

4
1 3 3 2 0
0 0
3 0
2 0

Sample Output 2

node 0: parent = 1, depth = 1, leaf, []
node 1: parent = -1, depth = 0, root, [3, 2, 0]
node 2: parent = 1, depth = 1, leaf, []
node 3: parent = 1, depth = 1, leaf, []

Note

You can use a left-child, right-sibling representation to implement a tree which has the following data:

• the parent of u
• the leftmost child of u
• the immediate right sibling of u

Reference

Introduction to Algorithms, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. The MIT Press.

有根树的存储, 根据数据看出不是二叉树, 故用孩子兄弟表示法存储(左孩子, 右兄弟)

利用递归求树的深度时, 若是左孩子则深度加一, 右孩子(兄弟节点)还是当前深度

#include <iostream>
using namespace std;
#define MAX 100005
#define NIL -1

struct Node {
	int parent;
	int left;
	int right;
}; 

Node T[MAX];
int n, D[MAX];

void print(int u)
{
	int i, c;
	cout << "node " << u << ": ";
	cout << "parent = " << T[u].parent << ", ";
	cout << "depth = " << D[u] << ", ";

	if(T[u].parent == NIL)
	{
		cout << "root, ";
	}
	else if(T[u].left == NIL)
	{
		cout << "leaf, ";
	}
	else
	{
		cout << "internal node, ";
	}

	cout << "[";

	for(i = 0, c = T[u].left; c != NIL; ++ i, c = T[c].right)
	{
		if(i)	cout << ", ";
		cout << c;
	}

	cout << "]" << endl;
}

// 递归求深度
void rec(int u, int p)
{
	D[u] = p;
	if(T[u].right != NIL)
	{
		rec(T[u].right, p);
	}
	if(T[u].left != NIL)
	{
		rec(T[u].left, p + 1);
	}
}

int main()
{
	int i, j, d, v, c, l, r;
	cin >> n;
	for(i = 0; i < n; ++ i)
	{
		T[i].parent = T[i].left = T[i].right = NIL;
	}

	for(i = 0; i < n; ++ i)
	{
		cin >> v >> d;
		for(j = 0; j < d; ++ j)
		{
			cin >> c;
			if(j == 0)
			{
				T[v].left = c;	// 父节点的左孩子为c
			}
			else
			{
				T[l].right = c;	// 当前兄弟节点为c
			}
			l = c;	// 记录前一个兄弟节点
			T[c].parent = v;
		}
	}
	for(i = 0; i < n; ++ i)
	{
		if(T[i].parent == NIL)
		{
			r = i;
		}
	}

	rec(r, 0);

	for(i = 0; i < n; ++ i)
	{
		print(i);
	}

	return 0;
}

/*
13
0 3 1 4 10
1 2 2 3
2 0
3 0
4 3 5 6 7
5 0
6 0
7 2 8 9
8 0
9 0
10 2 11 12
11 0
12 0
*/