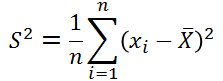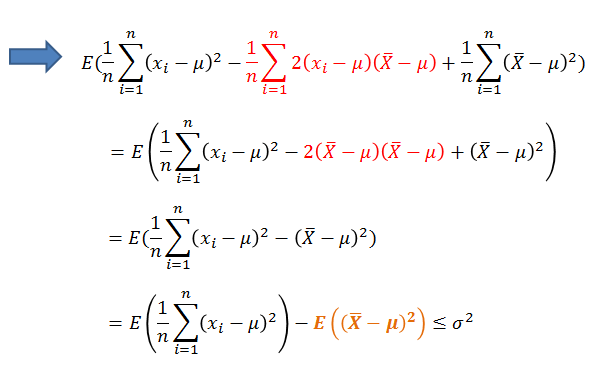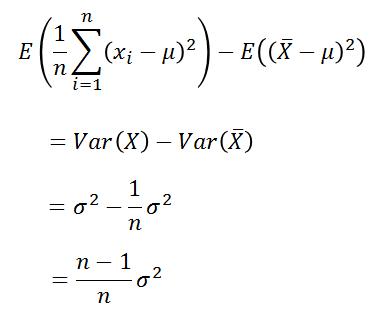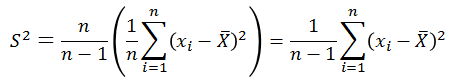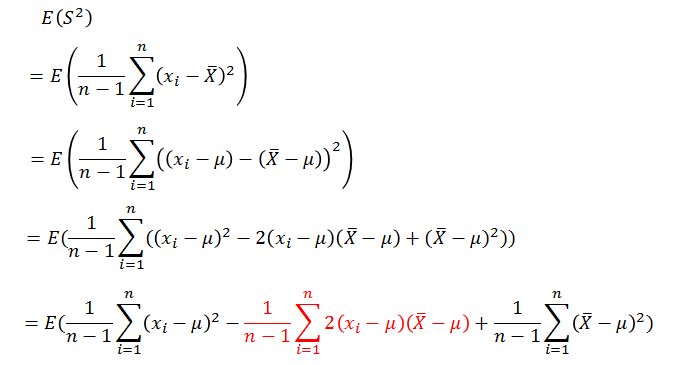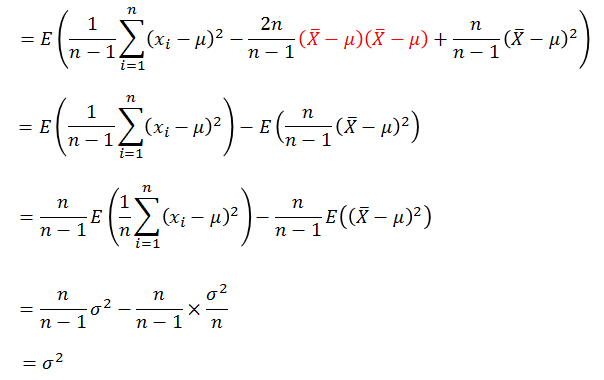无偏方差为什么除以n-1
设样本均值为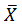
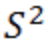 ,总体均值为
,总体均值为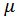
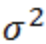 ,那么样本方差
,那么样本方差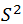
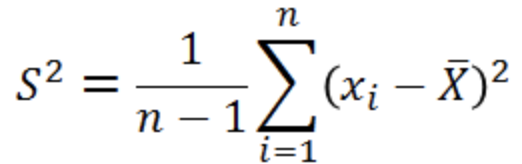
很多人可能都会有疑问,为什么要除以n-1,而不是n,但是翻阅资料,发现很多都是交代到,如果除以n,对样本方差的估计不是无偏估计,比总体方差要小,要想是无偏估计就要调小分母,所以除以n-1,那么问题来了,为什么不是除以n-2、n-3等等。所以在这里彻底总结一下,首先交代一下无偏估计。
无偏估计
以例子来说明,假如你想知道一所大学里学生的平均身高是多少,一个大学好几万人,全部统计有点不现实,但是你可以先随机挑选100个人,统计他们的身高,然后计算出他们的平均值,记为 。如果你只是把
。如果你只是把 作为整体的身高平均值,误差肯定很大,因为你再随机挑选出100个人,身高平均值很可能就跟刚才计算的不同,为了使得统计结果更加精确,你需要多抽取几次,然后分别计算出他们的平均值,分别记为:
作为整体的身高平均值,误差肯定很大,因为你再随机挑选出100个人,身高平均值很可能就跟刚才计算的不同,为了使得统计结果更加精确,你需要多抽取几次,然后分别计算出他们的平均值,分别记为: 然后在把这些平均值,再做平均,记为:
然后在把这些平均值,再做平均,记为: ,这样的结果肯定比只计算一次更加精确,随着重复抽取的次数增多,这个期望值会越来越接近总体均值
,这样的结果肯定比只计算一次更加精确,随着重复抽取的次数增多,这个期望值会越来越接近总体均值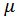
 ,这就是一个无偏估计,其中统计的样本均值也是一个随机变量,
,这就是一个无偏估计,其中统计的样本均值也是一个随机变量,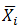
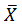
介绍无偏估计的意义就是,我们计算的样本方差,希望它是总体方差的一个无偏估计,那么假如我们的样本方差是如下形式:

那么,我们根据无偏估计的定义可得:

由上式可以看出如果除以n,那么样本方差比总体方差的值偏小,那么该怎么修正,使得样本方差式总体方差的无偏估计呢?我们接着上式继续化简:

到这里得到如下式子,看到了什么?该怎修正似乎有点眉目。

如果让我们假设的样本方差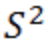
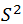
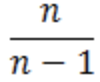
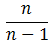
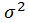

则:
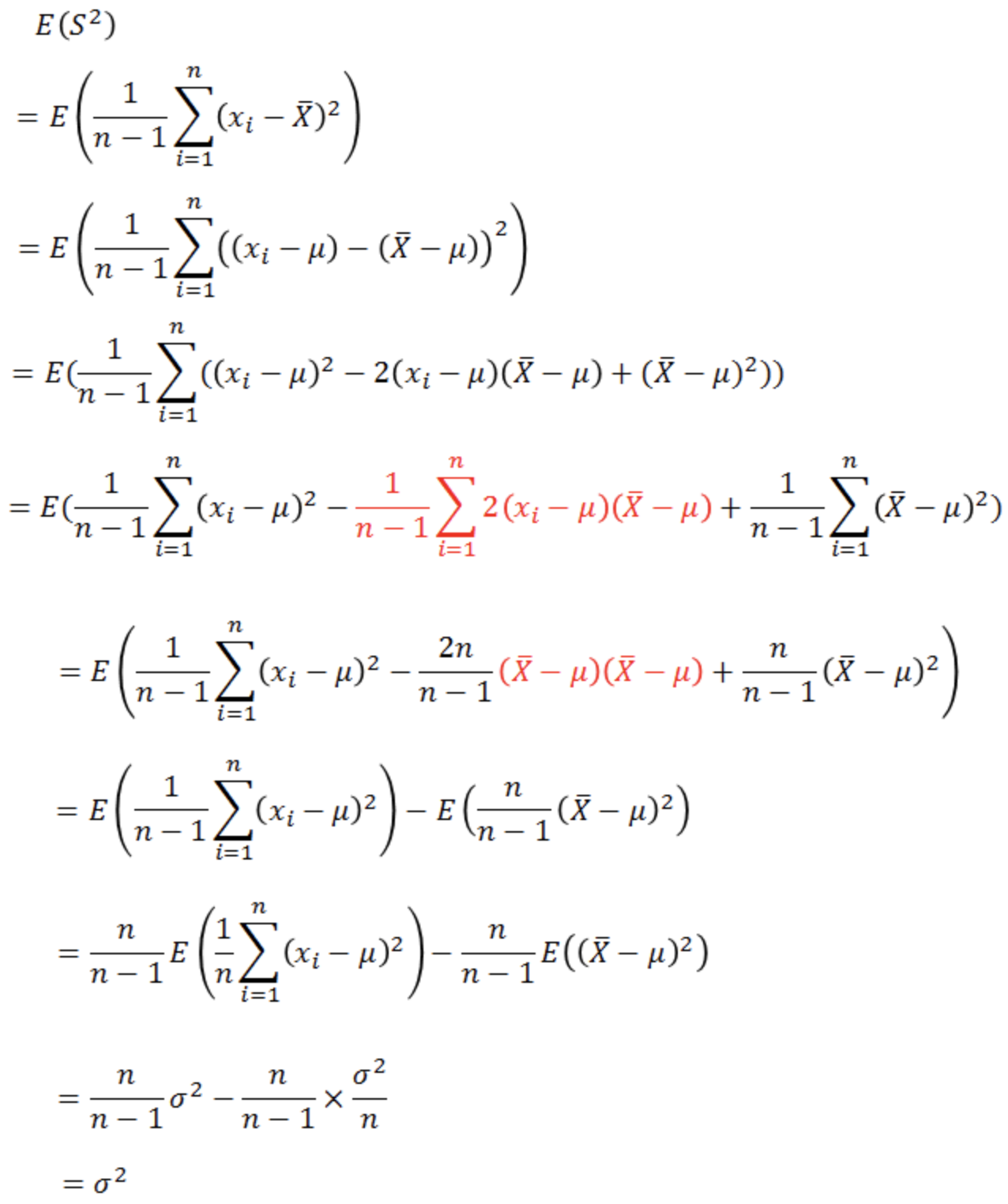
因此修正之后的样本方差的期望是总体方差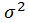
https://blog.csdn.net/hearthougan/article/details/77859173
无偏方差为什么除以n-1的更多相关文章
- 方差(variance)、标准差(Standard Deviation)、均方差、均方根值(RMS)、均方误差(MSE)、均方根误差(RMSE)
方差(variance).标准差(Standard Deviation).均方差.均方根值(RMS).均方误差(MSE).均方根误差(RMSE) 2017年10月08日 11:18:54 cqfdcw ...
- 【原创】开源Math.NET基础数学类库使用(10)C#进行基本数据统计
本博客所有文章分类的总目录:[总目录]本博客博文总目录-实时更新 开源Math.NET基础数学类库使用总目录:[目录]开源Math.NET基础数学类库使用总目录 前言 ...
- RapidJSON 代码剖析(四):优化 Grisu
我曾经在知乎的一个答案里谈及到 V8 引擎里实现了 Grisu 算法,我先引用该文的内容简单介绍 Grisu.然后,再谈及 RapidJSON 对它做了的几个底层优化. (配图中的<Grisù& ...
- 开源Math.NET基础数学类库使用(10)C#进行基本数据统计
原文:[原创]开源Math.NET基础数学类库使用(10)C#进行基本数据统计 本博客所有文章分类的总目录:http://www.cnblogs.com/asxinyu/p ...
- 【XSY2843】「地底蔷薇」 NTT什么的 扩展拉格朗日反演
题目大意 给定集合\(S\),请你求出\(n\)个点的"所有极大点双连通分量的大小都在\(S\)内"的不同简单无向连通图的个数对\(998244353\)取模的结果. \(n\le ...
- Pandas系列(七)-计算工具介绍
内容目录 1. 统计函数 2. 窗口函数 3. 加深加强 数据准备 # 导入相关库 import numpy as np import pandas as pd #Pandas 中包含了非常丰富的计算 ...
- 深度学习框架PyTorch一书的学习-第四章-神经网络工具箱nn
参考https://github.com/chenyuntc/pytorch-book/tree/v1.0 希望大家直接到上面的网址去查看代码,下面是本人的笔记 本章介绍的nn模块是构建与autogr ...
- Spark SQL 函数全集
org.apache.spark.sql.functions是一个Object,提供了约两百多个函数. 大部分函数与Hive的差不多. 除UDF函数,均可在spark-sql中直接使用. 经过impo ...
- GoogLeNetv2 论文研读笔记
Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift 原文链接 摘要 ...
随机推荐
- Ubuntu16.04更换NVIDIA驱动导致无法进入图形界面的解决方案
一.进入recovery模式 由于无法进入图形界面,所以需要在开机时进入恢复模式.我的机器上时在开机时通过引导选项中的recovery mode选项进入,进入之后可以看到许多选项卡,选择root,回车 ...
- Django 模型中FileField字段
FileField¶ class FileField([upload_to=None, max_length=100, **options])¶ 一个上传文件的字段. 注意 FileField字段不支 ...
- 「bzoj4264 小C找朋友」
权限题 就是一个集合\(hash\) 集合\(hash\)可以用于判断两个集合是否相等,具体做法就是给每个随机一个值,之后异或起来就是可以了 这个题就是这样,处理出每个点直接相连的点集的\(hash\ ...
- UVA151 Power Crisis
嘟嘟嘟 这道题被评为紫题完全是在假(虽然我也跟风评了紫题),顶多黄题难度. 评黄题的主要原因是得知道约瑟夫递推公式,即fn = (fn - 1 +m) % n.表示n个人报数最后的获胜者,需要注意的是 ...
- 使用appium在android9.0真机上测试程序时报错command failed shell “ps ‘uiautomator’”的解决办法
appium目前最新的windows版本是1.4.16,在android9.0真机上测试程序时会报错:command failed shell “ps ‘uiautomator’”. 网上大多数人的解 ...
- tomcat部署web项目方法
一.tomcat部署web项目之静态配置: 方法一:直接将为web项目放到webapps下: 如图所示:在webapps文件下,存放了一个html文件,启动tomcat,访问http://localh ...
- JDK自带监控工具
该篇文章,主要是工具普及,告诉大家有这么两款工具,可帮助我们进行JVM调优,及时看到JVM的变化. 不过建议,最好还是对于JVM相关的知识点,有一定的基础和熟悉. JDK自带jconsole.exe和 ...
- mybaitis动态sql利用bind标签代替%拼接完成模糊查询
Oracle中使用bind的写法 <select id="selectUser" resultType="user" parameterType=&quo ...
- SpringMVC使用校验validator校验对象属性
1.pom.xm添加依赖 <dependency> <groupId>javax.validation</groupId> <artifactId>va ...
- 如果js设置移动端有两种方式 大家可以参考
//使用em单位 var scaleObj = { documentEle : document.documentElement, deviceWidth : document.documentEle ...