【20161109】noip模拟赛

1．Game

【题目描述】

明明和亮亮在玩一个游戏。桌面上一行有n个格子，一些格子中放着棋子。明明和亮亮轮流选择如下方式中的一种移动棋子（图示中o表示棋子，*表示空着的格子）:

1） 当一枚棋子的右边是空格子的话，可以将这枚棋子像右移动一格。

**o***         ->           ***o**

2） 当一枚棋子的右边连续两个都有棋子，并且这个棋子往右边数第3格没有棋子，那么可以将这个棋子可以跳过去那两个棋子

**ooo*        ->           ***oo*

当任何一枚棋子到达最右边的格子时，这枚棋子自动消失。当一方不能移动时，这方输。假设明明和亮亮都采取最优策略，明明先走，谁将取胜？

【输入数据】

第一行一个整数T表示数据组数， 0 < T < 10。

之后T组数据，每组两行，第一行n 表示格子个数，第二行n个字符表示每个格子的情况，o表示有棋子，*表示空着。

【输出数据】

对于每组数据一个输出，M表示明明赢，L表示亮亮赢。

【样例输入】

4

2

*o

5

*o***

6

**o**o

14

*o***ooo**oo**

【样例输出】

L

M

M

L

【数据范围】

0 <T < 10

对于50%的数据， n < 20。

对于100%的数据， n < 1000。

---

第一题就博弈。。跪跪跪。。

真心不会博弈。。今晚好好重学一遍。。

看题解好像很好理解？？？

---

Game解题报告

对于前50%的数据，由于n<20，整个棋盘的状态个数 < 2^20。 由于状态数有限，我们可以采取记忆化搜索的办法来实现。

但对于100%的数据，n的最大可能值达到999，记忆化搜索就不怎么可行了。其实本题有一个更简单的做法：

考虑每个棋子到最右边格子的距离。把所有棋子这样的距离的总和计为s。我们发现不管选择两种操作中的一种操作，每走一步，s的奇偶性都会发生一次变化。所以说，如果第一次轮到明明时，s是奇数，那么每次轮到明明时s都是奇数。而当s是奇数时，s肯定>0，这时明明总可以走最右边的棋子。也就是说当s为奇数时，总有棋子可以走。所以说，一开始若s为奇数，则明明必胜。同理，若一开始s为偶数，则当亮亮走的时候s总是奇数，所以明明必败。

---

贴个代码：

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 using namespace std;

 const int N=,M=<<;
 int n,f[][M],a[N],b[N];
 char c[N],cc[N];

 int dfs(int x,int s)
 {
     if((s&)!=) s--;
     if(f[x][s]!=-) return f[x][s];
     int ss,ans=;
     for(int i=;i<n;i++)
     {
         if((s&(<<i))!= && (i->= && (s&(<<(i-)))==))
         {
             ss=s-(<<i)+(<<(i-));
             if(dfs(-x,ss)==) ans=;
         }
         if((s&(<<i))!= && (i->= && (s&(<<(i-)))!=) && (i->= && (s&(<<(i-)))!=) && (i->= && (s&(<<(i-)))==))
         {
             ss=s-(<<i)+(<<(i-));
             if(dfs(-x,ss)==) ans=;
         }
     }
     f[x][s]=ans;
     // printf("f %d %d = %d\n",x,s,ans);
     return ans;
 }

 void solve1()
 {
     scanf("%s",c);
     memset(f,-,sizeof(f));
     f[][]=f[][]=;
     int x=;
     for(int i=;i<n;i++)
     {
         if(c[i]=='o') x|=(<<(n--i));
     }
     // printf("x = %d\n",x);
     if(dfs(,x)==) printf("M\n");
     else printf("L\n");
 }

 void solve2()
 {
     scanf("%s",c+);
     int sum=;
     for(int i=;i<=n;i++)
     {
         if(c[i]=='o') sum+=n-i;
     }
     if(sum%==) printf("L\n");
     else printf("M\n");
 }

 int main()
 {
     // freopen("a.in","r",stdin);
     freopen("game.in","r",stdin);
     freopen("game.out","w",stdout);
     int T,x;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d",&n);
         if(n<=) solve1();
         else solve2();
     }
     return ;
 }

---

2．Walk

【题目描述】

有一块n *n 的土地上，明明和亮亮站在(1,1)处。每块地上写有一个数字a(i, j)。现在他们决定玩一个游戏，每一秒钟，他们俩走向相邻且坐标变大的格子（从(x,y)到(x+1,y)或者从(x,y)到(x,y+1)），他们俩可以按照不同方式来走，最后经过2n-1步到达(n,n)处。明明和亮亮每一秒钟计算他们站的两个位置上数字的差的绝对值，他们希望这些差值的和最大，请问这个最大的和是多少？

【输入数据】

第一行一个正整数n。

后面n行，每行n个整数，分别表示每块地上的数字。

【输出数据】

一个整数，表示最大的差值的和。

【样例输入】

4

1 2 3 4

1 5 3 2

8 1 3 4

3 2 1 5

【样例输出】

13

【数据范围】

n <= 100, 每块地上的数字的绝对值不超过300。

---

没什么好说的。就直接dp,f[i][j][k]表示走了i步，第一个人的横坐标是j，第二个人的横坐标是k。

通过走了i步可以算出纵坐标。

第一维只开了100又跪了。。

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 using namespace std;

 const int N=;
 int n,a[N][N],f[N][N][N];
 int dx[]={,};
 int dy[]={,};

 int myabs(int x){return x> ? x:-x;}
 int minn(int x,int y){return x<y ? x:y;}
 int maxx(int x,int y){return x>y ? x:y;}

 int main()
 {
     // freopen("a.in","r",stdin);
     freopen("walk.in","r",stdin);
     freopen("walk.out","w",stdout);
     scanf("%d",&n);
     for(int i=;i<n;i++)
         for(int j=;j<n;j++)
             scanf("%d",&a[i][j]);
     memset(f,-,sizeof(f));
     f[][][]=;
     int x1,y1,x2,y2,xx1,yy1,xx2,yy2;
     for(int i=;i<=*n-;i++)
         for(int j=;j<n;j++)
             for(int k=;k<n;k++)
             {
                 if(f[i][j][k]==-) continue;
                 // printf("f %d %d %d = %d\n",i,j,k,f[i][j][k]);
                 x1=j;y1=i-j;
                 x2=k;y2=i-k;
                 for(int ii=;ii<=;ii++)
                     for(int jj=;jj<=;jj++)
                     {
                         xx1=x1+dx[ii];yy1=y1+dy[ii];
                         xx2=x2+dx[jj];yy2=y2+dy[jj];
                         if(xx1>=n || yy1>=n || xx2>=n || yy2>=n) continue;
                         f[i+][xx1][xx2]=maxx(f[i+][xx1][xx2],f[i][x1][x2]+myabs(a[xx1][yy1]-a[xx2][yy2]));
                     }
             }
     printf("%d\n",f[*n-][n-][n-]);
     return ;
 }

---

3. Trip

【题目描述】

小朋友们出去郊游，明明和亮亮负责在草地上开一个篝火晚会。这个草地你可以认为是又 N * M 块单位长度为1的小正方形的草组成。

显然有的地方草长的好，有的地方长的不好，坐在上面显然舒服度是不一样的，于是每一块草都有一个舒服度 F。

现在明明和亮亮要选定一个 a*b 的草场作为晚会的地点，小朋友们就坐在上面，显然他希望小朋友们坐的最舒服！

不过别急，篝火晚会怎么能少了篝火呢，篝火需要占用 c*d 的草地，当然，篝火必须严格放置在选定的草地的内部，也就是说，篝火的边界不能和选定操场的边界有公共部分，不然学生们怎么围着篝火开晚会呢？

给定 N*M 大草地每一块的舒服度，寻找一个 a*b 的草地，除去一个严格内部的 c*d 的子草地，使得总的舒服度最大。

【输入数据】

第1行：6个整数，M ,  N,  b,   a,   d,   c

第2~N+1行：每行 M 个整数，第 i行j列的整数 Fi,j 表示，第 i行j列的单位草地的舒服度。

【输出数据】

一个整数，表示最大的舒服值。

【样例输入】

8 5 5 3 2 1

1 5 10 3 7 1 2 5

6 12 4 4 3 3 1 5

2 4 3 1 6 6 19 8

1 1 1 3 4 2 4 5

6 6 3 3 3 2 2 2

【样例输出】

70

【数据说明】

下面的图片就是对样例的解释，阴影区域就是最佳的选择方案。

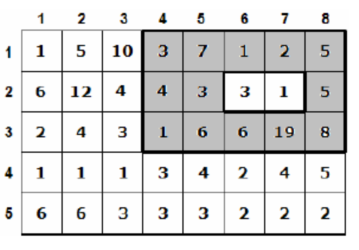
比如方案 4 1 4 1 就是显然非法的，因为篝火出现出现在了选定草地的边界，学生们无法严格围住篝火。

【数据范围】

1 ≤ Fi,j ≤ 100

3 ≤ a ≤ N

3 ≤ b ≤ M

1 ≤ c ≤ a-2

1 ≤ d ≤ b-2

对于 40% 的数据 N,M ≤ 10

对于 60% 的数据 N,M ≤ 150

对于 100% 的数据 N,M ≤ 1000

---

这题其实就是求一个矩阵里的最小值。

然后就可以行做一遍，列做一遍。

我们可以一行一行的求出每个连续b-d-1个c*d矩形的最小值。再基于这个最小值，一列一列的求出每个a*b大矩形中和最小的c*d矩形。这样我们就可以找到最优的舒服值了。本算法的时间复杂度是O(MN)。

原本用优先队列。。然后超时了4个点哭。。

然后用单调队列就巨快了。。orz。。

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<vector>
 #include<queue>
 using namespace std;

 const int N=;
 int n,m,A,B,C,D;
 int a[N][N],c[N][N],s[N][N],t[N][N],p[N][N],rr[N][N],R[N][N];
 struct node{int x,d;}q[N*N];

 int maxx(int x,int y){return x>y ? x:y;}

 void solve()
 {
     node k;
     int ind,l,r;
     for(int i=;i<=n;i++)
     {
         l=;r=;
         for(int j=;j+D-<=B-;j++)
         {
             k.x=j;k.d=p[i][j];
             while(q[r].d>k.d && l<=r) r--;
             q[++r]=k;
             ind=j;
         }
         for(int j=;j+B-<=m;j++)
         {
             while(q[l].x<j) l++;
             rr[i][j]=q[l].d;
             ind++;k.x=ind;k.d=p[i][ind];
             while(q[r].d>k.d && l<=r) r--;
             q[++r]=k;
         }
     }
     for(int i=;i<=m;i++)
     {
         l=;r=;
         for(int j=;j+C-<=A-;j++)
         {
             k.x=j;k.d=rr[j][i];
             while(q[r].d>k.d && l<=r) r--;
             q[++r]=k;
             ind=j;
         }
         for(int j=;j+A-<=n;j++)
         {
             while(q[l].x<j) l++;
             R[j][i]=q[l].d;
             ind++;k.x=ind;k.d=rr[ind][i];
             while(q[r].d>k.d && l<=r) r--;
             q[++r]=k;
         }
     }
     int ans=;
     for(int i=;i+A-<=n;i++)
         for(int j=;j+B-<=m;j++)
             ans=maxx(ans,t[i][j]-R[i+][j+]);
     printf("%d\n",ans);
 }

 int main()
 {
     // freopen("a.in","r",stdin);
     freopen("trip.in","r",stdin);
     freopen("trip.out","w",stdout);
     scanf("%d%d%d%d%d%d",&m,&n,&B,&A,&D,&C);
     for(int i=;i<=n;i++)
         for(int j=;j<=m;j++)
             scanf("%d",&a[i][j]);
     memset(s,,sizeof(s));
     for(int i=;i<=n;i++)
         for(int j=;j<=m;j++)
         {
             s[i][j]=s[i-][j]+s[i][j-]-s[i-][j-]+a[i][j];
         }
     for(int i=;i+A-<=n;i++)
         for(int j=;j+B-<=m;j++)
             t[i][j]=s[i+A-][j+B-]-s[i+A-][j-]-s[i-][j+B-]+s[i-][j-];
     for(int i=;i+C-<=n;i++)
         for(int j=;j+D-<=m;j++)
             p[i][j]=s[i+C-][j+D-]-s[i+C-][j-]-s[i-][j+D-]+s[i-][j-];
     solve();
     return ;
 }

---

点分治裸题。。

先找出树的重心，对于每个点维护一个到树的重心的乘积d[x]。

然后找经过树的重心的树链是否有乘积为k的。

然后分治算各个子树。

ps：学了奥爷爷的线性求逆元。。强啊。。

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<vector>
 #include<queue>
 using namespace std;

 typedef long long LL;
 const int N=,M=,mod=,INF=(int)1e9;
 int n,len,sl,tl,a1,a2;
 LL K,d[N],val[N],t[N],s[N],v[M],ny[M];
 int first[N],size[N],mark[N],id[M];
 struct node{
     int x,y,next;
 }a[*N];

 int minn(int x,int y){return x<y ? x:y;}

 LL quickpow(LL x,LL y)
 {
     LL ans=;
     while(y)
     {
         if(y&) ans=ans*x%mod;
         x=x*x%mod;
         y/=;
     }
     return ans;
 }

 int ins(int x,int y)
 {
     a[++len].x=x;a[len].y=y;
     a[len].next=first[x];first[x]=len;
 }

 void find_root(int x,int fa,int tot,int &root)
 {
     size[x]=;
     bool bk=;
     for(int i=first[x];i;i=a[i].next)
     {
         int y=a[i].y;
         if(mark[y] || y==fa) continue;
         find_root(y,x,tot,root);
         size[x]+=size[y];
         if(*size[y]>tot) bk=;
     }
     if(bk && *(tot-size[x])<=tot) root=x;
 }

 void DFS(int x,int fa,int root)
 {
     d[x]=d[fa]*val[x]%mod;
     t[++tl]=d[x];id[tl]=x;
     LL now=(ny[d[x]]*K%mod)*val[root]%mod;
     if(v[now])
     {
         int X=x,Y=v[now];
         if(X>Y) swap(X,Y);
         if(X<a1) a1=X,a2=Y;
         else if(X==a1 && Y<a2) a2=Y;
     }
     size[x]=;
     for(int i=first[x];i;i=a[i].next)
     {
         int y=a[i].y;
         if(mark[y] || y==fa) continue;
         DFS(y,x,root);
         size[x]+=size[y];
     }
 }

 int dfs(int x,int tot)
 {
     find_root(x,,tot,x);
     // printf("tot = %d  root = %d\n",tot,x);
     mark[x]=;
     sl=;s[++sl]=val[x];
     d[x]=val[x];
     for(int i=first[x];i;i=a[i].next)
     {
         int y=a[i].y;
         if(mark[y]==) continue;
         tl=;
         DFS(y,x,x);
         for(int j=;j<=tl;j++)
         {
             s[++sl]=t[j];
             if(v[t[j]]==) v[t[j]]=id[j];
             else v[t[j]]=minn(v[t[j]],id[j]);
         }
     }
     if(v[K])
     {
         int X=x,Y=v[K];
         if(X>Y) swap(X,Y);
         if(X<a1) a1=X,a2=Y;
         else if(X==a1 && Y<a2) a2=Y;
     }
     for(int i=;i<=sl;i++) v[s[i]]=;
     for(int i=first[x];i;i=a[i].next)
     {
         int y=a[i].y;
         if(mark[y]==) continue;
         dfs(y,size[y]);
     }
 }

 int main()
 {
     // freopen("a.in","r",stdin);
     freopen("multik.in","r",stdin);
     freopen("multik.out","w",stdout);
     scanf("%d%d",&n,&K);
     len=;a1=INF;a2=INF;
     memset(v,,sizeof(v));
     memset(mark,,sizeof(mark));
     memset(first,,sizeof(first));
     ny[]=;
     for(int i=;i<=mod;i++)
         ny[i]=(mod-(mod/i))*ny[mod%i]%mod;
         // ny[i]=quickpow(i,mod-2);
     for(int i=;i<=n;i++)
         scanf("%d",&val[i]);
     for(int i=;i<n;i++)
     {
         int x,y;
         scanf("%d%d",&x,&y);
         ins(x,y);
         ins(y,x);
     }
     dfs(,n);
     if(a1<INF) printf("%d %d\n",a1,a2);
     else printf("No solution\n");
     return ;
 }