H5C303

H5C303

1、CSS3



一些js功能可以通过css3实现。

坚持渐进增强原则。

另一侧：优雅降级hack

3、选择器

1）属性选择器：根据指定名称的属性来查找元素



E是元素

li[style]{

}//含style属性的li元素
li[class=cc]{

}
选择class属性为cc的li属性。注意不必加引号
li[class*=cc]{
}
查找拥有指定属性及相应值的Li元素,可以在任意位置
li[class^=cc]{
查找拥有指定的a属性并且该属性值以cc开头的li元素
}

在这里的开头和结尾不一定要是一个完整的单词。

2）伪类选择器

兄弟伪类：以某元素或兄弟元素的位置来获取元素的结构伪类



相对于父元素的结构伪类

都是相当于相应元素的父元素来说的

注意：E限定了被选择元素的类型，其他类型元素是不满足要求的。若第一个元素类型不是E，失效。此时，改用以下语句：



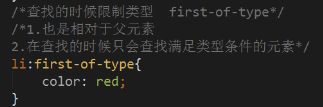
自动过滤不符合条件的元素，同样也有last-of-type





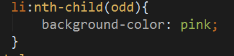
与之前类似，也有限制元素类型的of=type后缀的语句。



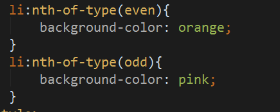
使用表达式：



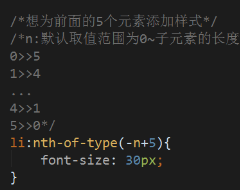
无法选取中间的元素

3）伪类样式target

结合锚点使用，处于当前锚点的元素会被选中

锚点：即href=‘id值’

4）伪类元素：before/after



伪元素并不在文档中生成。







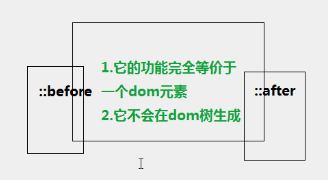
before与after仅示区分，表示各个dom元素都有该两个隐形的伪元素。

5）其他元素的使用

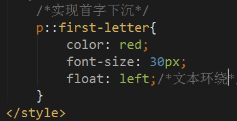
首字下沉：

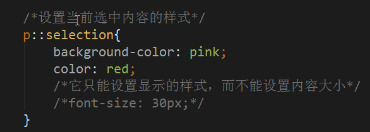
4、颜色模式

1）RGB ：



通过预设值或者是颜色拾取器可以进行颜色的设置

通过rgb设置：

background-color:rgb(红，绿，蓝)

2）HSL模式







3)设置透明 色的方式

利用opacity设置透明度会把该元素下的子元素的透明度都改变。

这时可利用rgba()中的最后一个参数设定透明度，将只改变当前元素的透明度

或者hsla()即可



5,文本阴影

可对文字产生阴影和模糊主体

看在css3之前可通过ps制作。

右键图层-投影









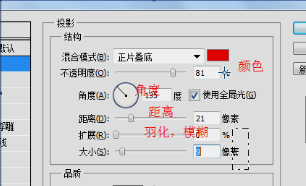
可依次设置多个阴影



这里有两点要注意：transparent是作为color的值，还有就是可以用rgba和hsla表示颜色。

6、盒模型

边框和padding值都是在盒子的外边追加，所以会把盒子撑大





设置box-sizing:border-box的样式即可

7、边框圆角

之前需要使用PS,非常不方便









每个角都各有两个方向的偏移可以设置。

案例：安卓机器人。