Christmas Spruce

　　Consider a rooted tree. A rooted tree has one special vertex called the root. All edges are directed from the root. Vertex u is called a child of vertex v and vertex v is called a parent of vertex u if there exists a directed edge from v to u. A vertex is called a leaf if it doesn't have children and has a parent.

　　Let's call a rooted tree a spruce if its every non-leaf vertex has at least 3 leaf children. You are given a rooted tree, check whether it's a spruce.

　　The definition of a rooted tree can be found here.

Input

　　The first line contains one integer n — the number of vertices in the tree (3 ≤ n ≤ 1 000). Each of the next n - 1 lines contains one integer pi (1 ≤ i ≤ n - 1) — the index of the parent of the i + 1-th vertex (1 ≤ pi ≤ i).

Vertex 1 is the root. It's guaranteed that the root has at least 2 children.

Output

　　Print "Yes" if the tree is a spruce and "No" otherwise.

Examples

input

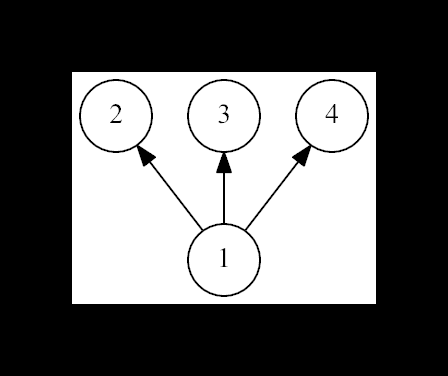
4
1
1
1

output

Yes

input

7
1
1
1
2
2
2

output

No

input

8
1
1
1
1
3
3
3

output

Yes

Note

The first example:

The second example:

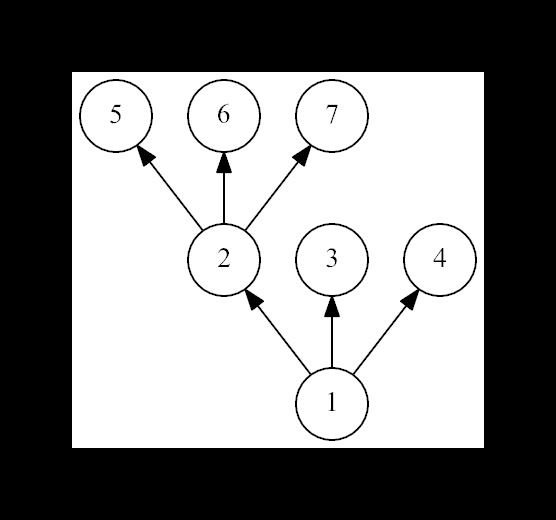
It is not a spruce, because the non-leaf vertex 1 has only 2 leaf children.

The third example:

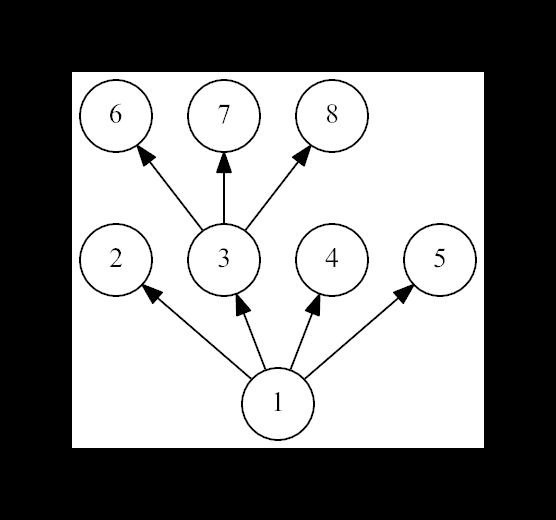
题意：给你一颗有根树，n个结点第一个结点为根结点。输入n-1行，代表从第二个结点开始的当前结点的父结点，例如样例一：第一个1代表2号结点父结点是1，

同理，3，4号父结点也是1。于是就连接成了样例一那种树。让我们判断每个非叶子结点的叶子个数是否 >=3 ，满足就输入Yes,否则就输出No.

分析：模拟，开个vis数组标记每个非叶子节点为1，叶子节点为0，从n到1扫一次，找叶子节点，就代表父结点有个满足条件的孩子。最后扫一次，扫每个非叶子节点，判断他的孩子是否>=3,就满足条件

输出yes.

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 using namespace std;
 const int maxn = ;
 int a[maxn],vis[maxn];

 int main(){
     int n;
     while(cin>>n){
         memset(vis,,sizeof(vis));
         for( int i=; i<=n; i++ ){
             cin>>a[i];
             vis[a[i]]=;//非叶子节点标记为1
         }
         for( int i=n; i>=; i-- ){
             if(!vis[i]) vis[a[i]]++;
         }
         int flag=;
         for( int i=; i<=n; i++ ){
             if(vis[i]&&vis[i]<){
                 flag=;
                 break;
             }
         }
         if(flag) cout<<"Yes"<<endl;
         else{
             cout<<"No"<<endl;
         }

     }
     return ;
 }