使用K-S检验一个数列是否服从正态分布、两个数列是否服从相同的分布

假设检验的基本思想：

若对总体的某个假设是真实的，那么不利于或者不能支持这一假设的事件A在一次试验中是几乎不可能发生的。如果事件A真的发生了，则有理由怀疑这一假设的真实性，从而拒绝该假设。

实质分析：

假设检验实质上是对原假设是否正确进行检验，因此检验过程中要使原假设得到维护，使之不轻易被拒绝；否定原假设必须有充分的理由。同时，当原假设被接受时，也只能认为否定该假设的根据不充分，而不是认为它绝对正确。

1、检验指定的数列是否服从正态分布

借助假设检验的思想，利用K-S检验可以对数列的性质进行检验，看代码：

from scipy.stats import kstest
import numpy as np

x = np.random.normal(0,1,1000)
test_stat = kstest(x, 'norm')

 

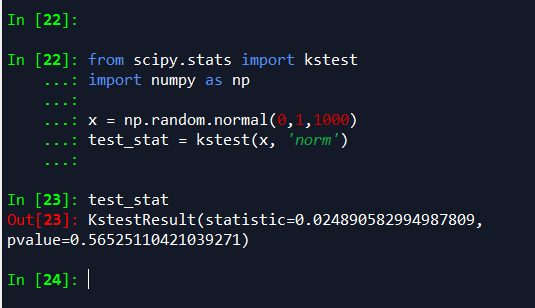
首先生成1000个服从N(0,1)标准正态分布的随机数，在使用k-s检验该数据是否服从正态分布，提出假设：x从正态分布。

最终返回的结果，p-value=0.76584491300591395，比指定的显著水平（假设为5%）大，则我们不能拒绝假设：x服从正态分布。

这并不是说x服从正态分布一定是正确的，而是说没有充分的证据证明x不服从正态分布。因此我们的假设被接受，认为x服从正态分布。

如果p-value小于我们指定的显著性水平，则我们可以肯定的拒绝提出的假设，认为x肯定不服从正态分布，这个拒绝是绝对正确的。

2、检验指定的两个数列是否服从相同分布

from scipy.stats import ks_2samp
beta=np.random.beta(7,5,1000)
norm=np.random.normal(0,1,1000)
ks_2samp(beta,norm)

　　

 

 

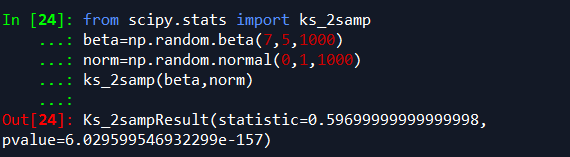
我们先分别使用beta分布和normal分布产生两个样本大小为1000的数列，使用ks_2samp检验两个数列是否来自同一个样本，提出假设：beta和norm服从相同的分布。

最终返回的结果，p-value=4.7405805465370525e-159，比指定的显著水平（假设为5%）小，则我们完全可以拒绝假设：beta和norm不服从同一分布。