高速公路 [HAOI2012] [线段树]

Description

Y901高速公路是一条重要的交通纽带，政府部门建设初期的投入以及使用期间的养护费用都不低，因此政府在这条高速公路上设立了许多收费站。
Y901高速公路是一条由N-1段路以及N个收费站组成的东西向的链，我们按照由西向东的顺序将收费站依次编号为1~N，从收费站i行驶到i+1(或从i+1行驶到i)需要收取Vi的费用。高速路刚建成时所有的路段都是免费的。
政府部门根据实际情况，会不定期地对连续路段的收费标准进行调整，根据政策涨价或降价。
无聊的小A同学总喜欢研究一些稀奇古怪的问题，他开车在这条高速路上行驶时想到了这样一个问题:对于给定的l,r(l＜r),在第l个到第r个收费站里等概率随机取出两个不同的收费站a和b，那么从a行驶到b将期望花费多少费用呢?

Input

第一行2个正整数N,M，表示有N个收费站，M次调整或询问
接下来M行，每行将出现以下两种形式中的一种
C l r v 表示将第l个收费站到第r个收费站之间的所有道路的通行费全部增加v
Q l r 表示对于给定的l,r，要求回答小A的问题
所有C与Q操作中保证1<=l l＜r,在第l个到第r个收费站里等概率随机取出两个不同的收费站a和b，那么从a行驶到b将期望花费多少费用呢?

Output

对于每次询问操作回答一行，输出一个既约分数
若答案为整数a，输出a/1

Sample Input

4 5
C 1 4 2
C 1 2 -1
Q 1 2
Q 2 4
Q 1 4

Sample Output

1/1
8/3
17/6

Hint

数据约束

所有C操作中的v的绝对值不超过10000

在任何时刻任意道路的费用均为不超过10000的非负整数

N,M<=1e5

Solution
对于一次询问，第i条边的贡献为 wi*(i-L+1)*(R-i+1)

可以这么理解，在i的左边（包括自身）选择起点，在i的右边（包括自身）选择终点，相乘即为组合的个数

然后

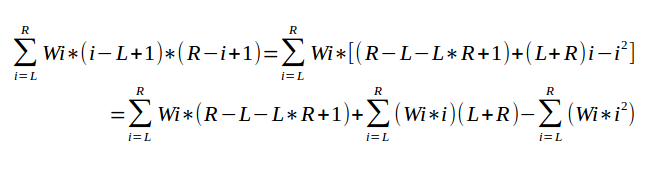
我们就可以看出，用线段树分别维护三个值：S0:∑wi , S1:∑(wi*i) , S2:∑(wi*i²)即可

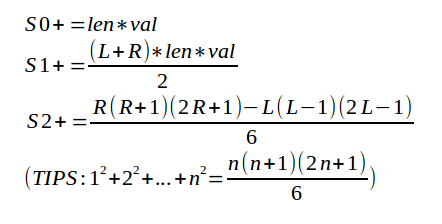（S2漏乘了一个val）

这个该死的线段树调了我两个小时。以后打线段树还是要小心一点慢点打 = =

Code

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #define RG register int
 #define rep(i,a,b)    for(RG i=a;i<=b;i++)
 #define per(i,a,b)    for(RG i=a;i>=b;i--)
 #define inf (1<<30)
 #define maxn 100005
 #define ll long long
 #define ls pos<<1
 #define rs pos<<1|1
 #define L t[pos].l
 #define R t[pos].r
 #define mid ((t[pos].l+t[pos].r)>>1)
 #define cal0(x,y) x*y
 #define cal1(x,y,z,w) (x+y)*z*w/2ll
 #define cal2(x,y,z) (y*(y+1ll)*(2ll*y+1ll)-x*(x-1ll)*(2ll*x-1ll))*z/6ll //bug
 using namespace std;
 int n,m;
 struct T{
     int l,r;
     ll s0,s1,s2,tag;
 }t[maxn<<];
 struct Dat{
     ll a0,a1,a2;
     inline Dat operator + (const Dat x)const{
         return (Dat){a0+x.a0,a1+x.a1,a2+x.a2};
     }
 };
 inline int read()
 {
     int x=,f=;char c=getchar();
     while(c<''||c>''){if(c=='-')f=-;c=getchar();}
     while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
     return x*f;
 }

 void build(int pos,int l,int r)
 {
     t[pos].l=l,t[pos].r=r;
     if(l==r)    return;
     build(ls,l,mid);build(rs,mid+,r);
 }

 inline void pushdown(int pos)
 {
     t[ls].tag+=t[pos].tag,t[rs].tag+=t[pos].tag;
     ll len1=t[ls].r-t[ls].l+,len2=t[rs].r-t[rs].l+;//bug

     t[ls].s0+=cal0(len1,t[pos].tag),
     t[ls].s1+=cal1(t[ls].l,t[ls].r,len1,t[pos].tag),
     t[ls].s2+=cal2(t[ls].l,t[ls].r,t[pos].tag);

     t[rs].s0+=cal0(len2,t[pos].tag),
     t[rs].s1+=cal1(t[rs].l,t[rs].r,len2,t[pos].tag),
     t[rs].s2+=cal2(t[rs].l,t[rs].r,t[pos].tag);

     t[pos].tag=;
 }

 void update(int pos,int l,int r,ll val)
 {
     if(l<=L&&R<=r)
     {
         ll len=R-L+;
         t[pos].s0+=cal0(len,val),
         t[pos].s1+=cal1(L,R,len,val),
         t[pos].s2+=cal2(L,R,val);
         t[pos].tag+=val;
         return;
     }
     if(t[pos].tag)     pushdown(pos);
     if(l<=mid)        update(ls,l,r,val);//bug
     if(r>mid)        update(rs,l,r,val);//bug
     t[pos].s0=t[ls].s0+t[rs].s0,
     t[pos].s1=t[ls].s1+t[rs].s1,
     t[pos].s2=t[ls].s2+t[rs].s2;
 }

 Dat query(int pos,int l,int r)
 {
     if(l<=t[pos].l&&t[pos].r<=r)
         return (Dat){t[pos].s0,t[pos].s1,t[pos].s2};
     if(t[pos].tag)    pushdown(pos);
     Dat ans=(Dat){,,};
     if(l<=mid)    ans=query(ls,l,r);
     if(r>mid)    ans=ans+query(rs,l,r);
     return ans;
 }

 ll gcd(ll a,ll b){return (!(a%b)?b:gcd(b,a%b));}

 int main()
 {
     n=read(),m=read();
     build(,,n-);
     char opt[];
     register ll l,r,v;
     rep(i,,m)
     {
         scanf("%s",opt);
         if(opt[]=='C')
         {
             l=read(),r=read()-,v=read();
             update(,l,r,v);
         }
         else
         {
             l=read(),r=read()-;
             Dat ans=query(,l,r);
             ll up=ans.a0*(r-l-l*r+1ll)+ans.a1*(l+r)-ans.a2;
             ll down=(r-l+1ll)*(r-l+2ll)/2ll;
             ll gd=gcd(up,down);
             up/=gd,down/=gd;
             printf("%lld/%lld\n",up,down);
         }
     }
     return ;
 }