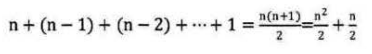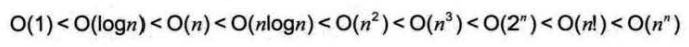【Algorithm】-NO.140.Algorithm.1.Algorithm.1.001-【空间复杂度 时间复杂度 o(1), o(n), o(logn), o(nlogn)】-
Style:Mac
Series:Java
Since:2018-09-10
End:2018-09-10
Total Hours:1
Degree Of Diffculty:5
Degree Of Mastery:5
Practical Level:5
Desired Goal:5
Archieve Goal:3
Gerneral Evaluation:3
Writer:kingdelee
Related Links:
http://www.cnblogs.com/kingdelee/
https://blog.csdn.net/daijin888888/article/details/66970902
在描述算法复杂度时,经常用到o(1), o(n), o(logn), o(nlogn)来表示对应算法的时间复杂度, 这里进行归纳一下它们代表的含义:
这是算法的时空复杂度的表示。
不仅仅用于表示时间复杂度,也用于表示空间复杂度。
O后面的括号中有一个函数,指明某个算法的耗时/耗空间与数据增长量之间的关系,其中的n代表输入数据的量。
比如时间复杂度为O(n),就代表数据量增大几倍,耗时也增大几倍。比如常见的遍历算法。
再比如时间复杂度O(n^2),就代表数据量增大n倍时,耗时增大n的平方倍,这是比线性更高的时间复杂度。比如冒泡排序,就是典型的O(n^2)的算法,对n个数排序,需要扫描n×n次。
再比如O(logn),当数据增大n倍时,耗时增大logn倍(这里的log是以2为底的,比如,当数据增大256倍时,耗时只增大8倍,是比线性还要低的时间复杂度)。二分查找就是O(logn)的算法,每找一次排除一半的可能,256个数据中查找只要找8次就可以找到目标。
O(nlogn)同理,就是n乘以logn,当数据增大256倍时,耗时增大256*8=2048倍。这个复杂度高于线性低于平方。归并排序就是O(nlogn)的时间复杂度。
O(1)就是最低的时空复杂度了,也就是耗时/耗空间与输入数据大小无关,无论输入数据增大多少倍,耗时/耗空间都不变。 哈希算法就是典型的O(1)时间复杂度,无论数据规模多大,都可以在一次计算后找到目标(不考虑冲突的话)
举例
一组数据的数据量为10000,查找算法耗时2s,当数据量增大100倍时,n为100,即100W的数据
则0(n),耗时增大100倍,耗时为200s
0(n^2),耗时增大100^2,即10000,耗时为2000000s
0(logn),耗时增大log100,对数是6.6,即增大6.6倍,耗时为13.2s
O(nlogn),耗时增大100*log100,即增大100*6.6倍=660倍,耗时为660*2=1320s
一、算法的时间复杂度定义
在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)随n的变化情况并确定T(n)的数量级。算法的时间复杂度,也就是算法的时间量度。记作:T(n)=O(f(n))。它表示随问题n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐进时间复杂度,简称为时间复杂度。其中,f(n)是问题规模n的某个函数。
这样用大写O()来体现算法时间复杂度的记法,我们称之为大0记法。
二、推导大O阶方法
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
三、推导示例
1、常数阶
首先顺序结构的时间复杂度。下面这个算法,是利用高斯定理计算1,2,……n个数的和。
- int sum = 0, n = 100; /*执行一次*/
- sum = (1 + n) * n / 2; /*执行一次*/
- printf("%d",sum); /*执行一次*/
这个算法的运行次数函数是f (n) =3。 根据我们推导大0阶的方法,第一步就是把常数项3 改为1。在保留最高阶项时发现,它根本没有最高阶项,所以这个算法的时间复杂度为0(1)。
另外,我们试想一下,如果这个算法当中的语句 sum = (1+n)*n/2; 有10 句,则与示例给出的代码就是3次和12次的差异。这种与问题的大小无关(n的多少),执行时间恒定的算法,我们称之为具有O(1)的时间复杂度,又叫常数阶。对于分支结构而言,无论是真,还是假,执行的次数都是恒定的,不会随着n 的变大而发生变化,所以单纯的分支结构(不包含在循环结构中),其时间复杂度也是0(1)。
2、线性阶
线性阶的循环结构会复杂很多。要确定某个算法的阶次,我们常常需要确定某个特定语句或某个语句集运行的次数。因此,我们要分析算法的复杂度,关键就是要分析循环结构的运行情况。
下面这段代码,它的循环的时间复杂度为O(n), 因为循环体中的代码须要执行n次。
- int i;
- for(i = 0; i < n; i++){
- /*时间复杂度为O(1)的程序步骤序列*/
- }
3、对数阶
如下代码:
- int count = 1;
- while (count < n){
- count = count * 2;
- /*时间复杂度为O(1)的程序步骤序列*/
- }
4、平方阶
下面例子是一个循环嵌套,它的内循环刚才我们已经分析过,时间复杂度为O(n)。
- int i, j;
- for(i = 0; i < n; i++){
- for(j = 0; j < n; j++){
- /*时间复杂度为O(1)的程序步骤序列*/
- }
- }
而对于外层的循环,不过是内部这个时间复杂度为O(n)的语句,再循环n次。 所以这段代码的时间复杂度为O(n^2)。
如果外循环的循环次数改为了m,时间复杂度就变为O(mXn)。
所以我们可以总结得出,循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数。
那么下面这个循环嵌套,它的时间复杂度是多少呢?
- int i, j;
- for(i = 0; i < n; i++){
- for(j = i; j < n; j++){ /*注意j = i而不是0*/
- /*时间复杂度为O(1)的程序步骤序列*/
- }
- }
由于当i=0时,内循环执行了n次,当i = 1时,执行了n-1次,……当i=n-1时,执行了1次。所以总的执行次数为:
用我们推导大O阶的方法,第一条,没有加法常数不予考虑;第二条,只保留最高阶项,因此保留时(n^2)/2; 第三条,去除这个项相乘的常数,也就是去除1/2,最终这段代码的时间复杂度为O(n2)。
从这个例子,我们也可以得到一个经验,其实理解大0推导不算难,难的是对数列的一些相关运算,这更多的是考察你的数学知识和能力。
5、立方阶
下面例子是一个三重循环嵌套。
- int i, j;
- for(i = 1; i < n; i++)
- for(j = 1; j < n; j++)
- for(j = 1; j < n; j++){
- /*时间复杂度为O(1)的程序步骤序列*/
- }
这里循环了(1^2+2^2+3^2+……+n^2) = n(n+1)(2n+1)/6次,按照上述大O阶推导方法,时间复杂度为O(n^3)。
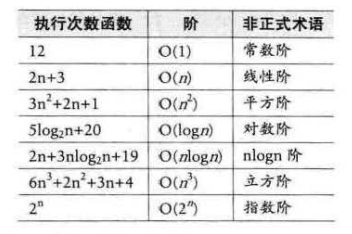
四、常见的时间复杂度
常见的时问复杂度如表所示。
常用的时间复杂度所耗费的时间从小到大依次是:
我们前面已经谈到了。O(1)常数阶、O(logn)对数阶、O(n)线性阶、 O(n^2)平方阶等,像O(n^3),过大的n都会使得结果变得不现实。同样指数阶O(2^n)和阶乘阶O(n!)等除非是很小的n值,否则哪怕n 只是100,都是噩梦般的运行时间。所以这种不切实际的算法时间复杂度,一般我们都不去讨论。
五、最坏情况与平均情况
我们查找一个有n 个随机数字数组中的某个数字,最好的情况是第一个数字就是,那么算法的时间复杂度为O(1),但也有可能这个数字就在最后一个位置上待着,那么算法的时间复杂度就是O(n),这是最坏的一种情况了。
最坏情况运行时间是一种保证,那就是运行时间将不会再坏了。 在应用中,这是一种最重要的需求, 通常, 除非特别指定, 我们提到的运行时间都是最坏情况的运行时间。
而平均运行时间也就是从概率的角度看, 这个数字在每一个位置的可能性是相同的,所以平均的查找时间为n/2次后发现这个目标元素。平均运行时间是所有情况中最有意义的,因为它是期望的运行时间。也就是说,我们运行一段程序代码时,是希望看到平均运行时间的。可现实中,平均运行时间很难通过分析得到,一般都是通过运行一定数量的实验数据后估算出来的。一般在没有特殊说明的情况下,都是指最坏时间复杂度。
六、算法空间复杂度
我们在写代码时,完全可以用空间来换取时间,比如说,要判断某某年是不是闰年,你可能会花一点心思写了一个算法,而且由于是一个算法,也就意味着,每次给一个年份,都是要通过计算得到是否是闰年的结果。 还有另一个办法就是,事先建立一个有2050个元素的数组(年数略比现实多一点),然后把所有的年份按下标的数字对应,如果是闰年,此数组项的值就是1,如果不是值为0。这样,所谓的判断某一年是否是闰年,就变成了查找这个数组的某一项的值是多少的问题。此时,我们的运算是最小化了,但是硬盘上或者内存中需要存储这2050个0和1。这是通过一笔空间上的开销来换取计算时间的小技巧。到底哪一个好,其实要看你用在什么地方。
算法的空间复杂度通过计算算法所需的存储空间实现,算法空间复杂度的计算公式记作:S(n)= O(f(n)),其中,n为问题的规模,f(n)为语句关于n所占存储空间的函数。
一般情况下,一个程序在机器上执行时,除了需要存储程序本身的指令、常数、变量和输入数据外,还需要存储对数据操作的存储单元,若输入数据所占空间只取决于问题本身,和算法无关,这样只需要分析该算法在实现时所需的辅助单元即可。若算法执行时所需的辅助空间相对于输入数据量而言是个常数,则称此算法为原地工作,空间复杂度为0(1)。
通常, 我们都使用"时间复杂度"来指运行时间的需求,使用"空间复杂度"指空间需求。当不用限定词地使用"复杂度'时,通常都是指时间复杂度。
七、一些计算的规则
1、加法规则
T(n,m) = T1(n) + T2(m) = O(max{f(n), g(m)})
2、乘法规则
T(n,m) = T1(n) * T2(m) = O(max{f(n)*g(m)})
3、一个经验
复杂度与时间效率的关系:

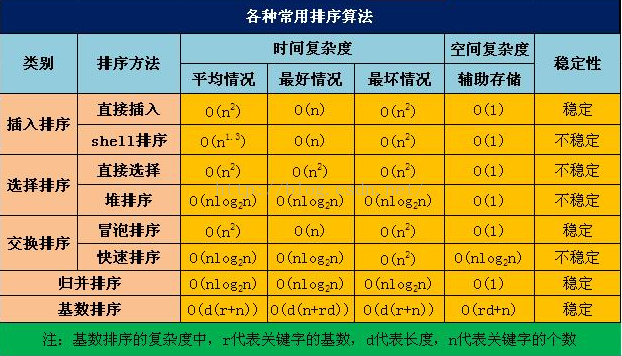
八、常用算法的时间复杂度和空间复杂度
---------------------
本文来自 皮卡丘啾啾 的CSDN 博客 ,全文地址请点击:https://blog.csdn.net/daijin888888/article/details/66970902?utm_source=copy
【Algorithm】-NO.140.Algorithm.1.Algorithm.1.001-【空间复杂度 时间复杂度 o(1), o(n), o(logn), o(nlogn)】-的更多相关文章
- PatentTips - Adaptive algorithm for selecting a virtualization algorithm in virtual machine environments
BACKGROUND A Virtual Machine (VM) is an efficient, isolated duplicate of a real computer system. Mor ...
- SPOJ 5152 Brute-force Algorithm EXTREME && HDU 3221 Brute-force Algorithm 快速幂,快速求斐波那契数列,欧拉函数,同余 难度:1
5152. Brute-force Algorithm EXTREME Problem code: BFALG Please click here to download a PDF version ...
- [Algorithm] Breadth First JavaScript Search Algorithm for Graphs
Breadth first search is a graph search algorithm that starts at one node and visits neighboring node ...
- [Algorithm] Beating the Binary Search algorithm – Interpolation Search, Galloping Search
From: http://blog.jobbole.com/73517/ 二分检索是查找有序数组最简单然而最有效的算法之一.现在的问题是,更复杂的算法能不能做的更好?我们先看一下其他方法. 有些情况下 ...
- BSS Audio® Introduces Full-Bandwidth Acoustic Echo Cancellation Algorithm for Soundweb London Conferencing Processors
BSS Audio® Introduces Full-Bandwidth Acoustic Echo Cancellation Algorithm for Soundweb London Confer ...
- 人脸识别算法准确率最终超过了人类 The Face Recognition Algorithm That Finally Outperforms Humans
Everybody has had the experience of not recognising someone they know—changes in pose, illumination ...
- MR for Baum-Welch algorithm
The Baum-Welch algorithm is commonly used for training a Hidden Markov Model because of its superior ...
- [Algorithm] 如何正确撸<算法导论>CLRS
其实算法本身不难,第一遍可以只看伪代码和算法思路.如果想进一步理解的话,第三章那些标记法是非常重要的,就算要花费大量时间才能理解,也不要马马虎虎略过.因为以后的每一章,讲完算法就是这样的分析,精通的话 ...
- Expanded encryption and decryption signature algorithm SM2 & SM3
Expanded encryption and decryption signature algorithm supports multiple signature digest algorithms ...
随机推荐
- logrus日志使用详解
1.logrus特点 golang标准库的日志框架很简单,logrus框架的特点: 1)完全兼容标准日志库 六种日志级别:debug, info, warn, error, fatal, panic ...
- iOS 更改状态栏颜色和隐藏状态栏
更改状态栏颜色 iOS7以后 状态栏的字体为黑色:UIStatusBarStyleDefault 状态栏的字体为白色:UIStatusBarStyleLightContent 解决方案 1.在info ...
- 大话Json对象和Json字符串
一.Json对象和Json字符串的区别 (1)Json对象:可以通过javascript存取属性. 先介绍一下json对象,首先说到对象的概念,对象的属性是可以用:对象.属性进行调用的.例如: var ...
- 第四百零二节,Django+Xadmin打造上线标准的在线教育平台—生产环境部署,uwsgi安装和启动,nginx的安装与启动,uwsgi与nginx的配置文件+虚拟主机配置
第四百零二节,Django+Xadmin打造上线标准的在线教育平台—生产环境部署,uwsgi安装和启动,nginx的安装与启动,uwsgi与nginx的配置文件+虚拟主机配置 软件版本 uwsgi- ...
- 【Tensorflow】tensorboard
tbCallBack = tf.keras.callbacks.TensorBoard(log_dir='./log' , histogram_freq=0, write_graph=True, wr ...
- mui---获取设备的网络状态
在用mui做音乐或视频播放器的时候,往往会考虑当前音乐+视频的播放环境.例如是4G ,WIFI,无网络,给出特定的提示: 具体做法:根据 getCurrentType来进行获取当前网络的类型: plu ...
- python argparse sys.argv
python argparse sys.argv class WeiLearningArgumentParser(argparse.ArgumentParser): def __init__(self ...
- Python学习之旅(八)
Python基础知识(7):数据基本类型之元组.字典 一.元组 用括号把元素括起来中间用逗号隔开.用逗号分开一些值便可创建元组 1,2,3 结果: (1, 2, 3) 空元组可以用没有包含任何内容的两 ...
- python语法_注释
#加需要注释的内容,#号后面的单行注释 #这一段注释 左右各三个注释单引号或者双引号 中间的内容为注释,可以包含多行 '''这一段注释''' """这一段注释" ...
- 微信OAuth授权获取用户OpenId-JAVA(个人经验)【申明:来源于网络】
微信OAuth授权获取用户OpenId-JAVA(个人经验)[申明:来源于网络] 地址:https://my.oschina.net/xshuai/blog/293458