lamada 表达式

语法篇 -- \(lamada\) 表达式

函数内定义的函数，看起来能使代码更加美观。

具体定义方法：

1. 前面挂个 auto ，不管他返不返回值

2. 后面是函数名(表达式名) 例: Cekas

3. 先是中括号表示对外部环境的调用：
   
   具体看下表：

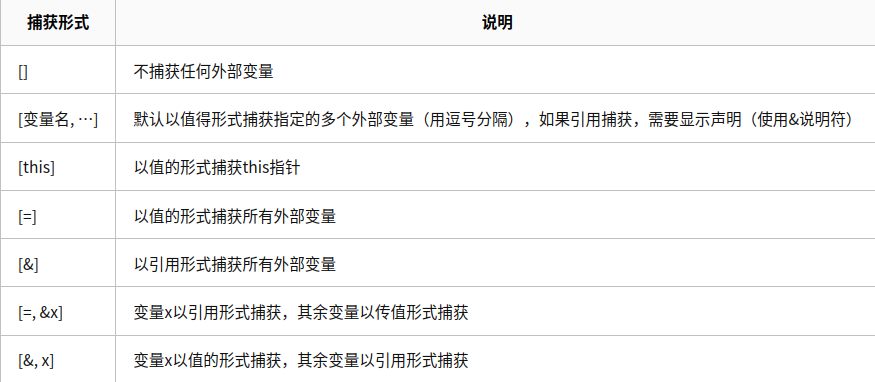
1. 可能你是以值捕获的外部变量，你在 \(lamada\) 体中更改后程序会报错，这时就需要 mutable 关键字这就可以更改了。

具体打法：

auto f1 = [a](int al)mutable {
    a ++ ; // 过编
    cout << a ;
} ; 

f1() ; 

-------

auto f1 = [a](int al) {
    a ++ ; // 编译失败
    cout << a ;
} ; 

f1() ; 

1. Lambda表达式的异常说明符值为 \(noexcept\) ，其意义是指明表达式不会抛出异常；如果不需要此操作，则可以省略此项。

意思是只要你不 throw 就可以打 noexcept , 不打也不会死。

结尾撒花 \(\color{pink}✿✿ヽ(°▽°)ノ✿\)