#排列组合#C 模拟比赛

---

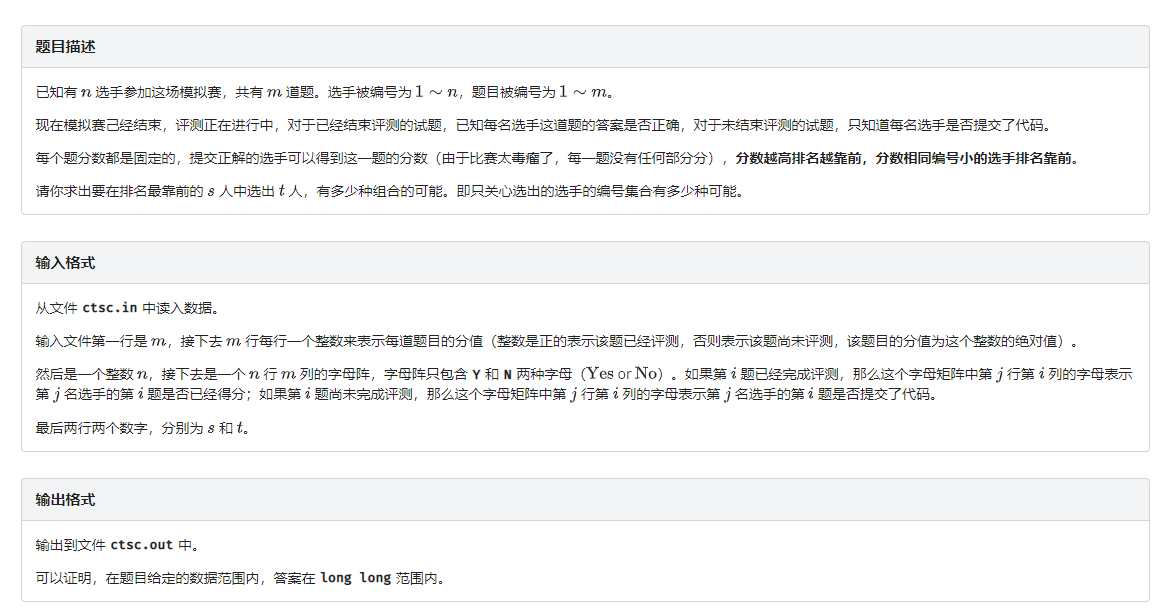
分析

由于每个选手的得分独立，考虑按照选手的最高得分降序排序

如果当前枚举到选手\(i\),首先记录\(o_i\)表示在选手\(i\)之前最小得分不低于选手\(i\)的最高得分

（必选，等于必选当且仅当编号比选手\(i\)的原编号小）

然后再枚举从这些必选的当中选择的数量\(j\)，那么统计的答案即为\(C_{o_i}^{j}\times C_{i-1-o_i}^{t-j-1}\)

注意枚举的\(k\)也有限制条件

---

代码

#include <cstdio>
#include <cctype>
#include <algorithm>
#define rr register
using namespace std;
const int N = 51;
typedef long long lll;
struct rec {
    int rk, mn, mx;
} b[N];
int m, n, a[N], S, T;
lll c[N][N], ans;
inline signed iut() {
    rr int ans = 0, f = 1;
    rr char c = getchar();
    while (!isdigit(c)) f = (c == '-') ? -f : f, c = getchar();
    while (isdigit(c)) ans = (ans << 3) + (ans << 1) + (c ^ 48), c = getchar();
    return ans * f;
}
inline signed min(int a, int b) { return a < b ? a : b; }
inline signed max(int a, int b) { return a > b ? a : b; }
bool cmp(rec x, rec y) { return x.mx != y.mx ? x.mx > y.mx : x.rk < y.rk; }
signed main() {
    freopen("ctsc.in", "r", stdin);
    freopen("ctsc.out", "w", stdout);
    m = iut(), c[0][0] = 1;
    for (rr int i = 1; i <= m; ++i) a[i] = iut();
    n = iut();
    for (rr int i = 1; i <= n; ++i) c[i][0] = 1;
    for (rr int i = 1; i <= n; ++i)
        for (rr int j = 1; j <= i; ++j) c[i][j] = c[i - 1][j - 1] + c[i - 1][j];
    for (rr int i = 1; i <= n; ++i) {
        rr int MN = 0, MX = 0;
        for (rr int j = 1; j <= m; ++j) {
            rr char c = getchar();
            while (c != 'N' && c != 'Y') c = getchar();
            if (c == 'N')
                continue;
            if (a[j] < 0)
                MX -= a[j];
            else
                MN += a[j], MX += a[j];
        }
        b[i] = (rec){ i, MN, MX };
    }
    S = iut(), T = iut(), sort(b + 1, b + 1 + n, cmp);
    for (rr int i = 1; i <= n; ++i) {
        rr int o = 0;
        for (rr int j = 1; j < i; ++j)
            if (b[j].mn > b[i].mx || (b[j].mn == b[i].mx && b[j].rk < b[i].rk))
                ++o;
        if (o >= S)
            continue;//必选超过S人一定不行
        for (rr int j = max(T + o - S, 0); j <= min(o, T - 1); ++j) ans += c[o][j] * c[i - 1 - o][T - j - 1];//上界很容易理解，下界因为oi-j>s-t说明我没有的必选超过前s个没有被选择的个数说明不合法
    }
    return !printf("%lld", ans);
}