NumPy从入门到放弃

看前建议：

本文以jupyter notebook为编辑器进行示例，建议有一定python基础后再进行学习。

python的安装：https://www.cnblogs.com/scfssq/p/17478132.html

jupyter notebook的安装：https://www.cnblogs.com/kohler21/p/18349764

公众号本文地址：https://mp.weixin.qq.com/s/EocThNWhQlI2zeLcUApsQQ

NumPy简介

公众号：愚生浅末

Numeric Python（简称NumPy）是使用Python进行科学计算的基本包，它是一个Python库，提供了多维数组对象，使用NumPy相较于直接编写Python代码实现，性能更加高效、代码更加简洁。NumPy广泛应用于各类场合，例如在机器学习、数值处理、爬虫等。NumPy主要是围绕Ndarray对象展开，通过NumPy的线性代数库对其进行一系列操作如切片索引、广播、修改数组（形状、维度、元素的增删改）、连接数组等，以及对多维数组的点积等。除了数组，Numpy还有很多函数包括三角函数、统计函数等。

NumPy的重要特点之一就是 n 维数组对象，即 ndarray。

在使用Numpy之前需要线导入Numpy：

import numpy as np

生成数组

生成0\1数组

生成0/1数组，利用np.ones(shape, dtype)或np.ones_like(a, shape)、np.zeros(shape, dtype)或np.zeros_like(a, shape)

one_matrix = np.ones([3, 3]) # 生成一个3x3的矩阵，矩阵元素都为1

one_matrix

效果：

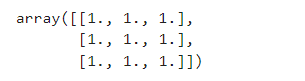
生成一个3x3的矩阵，矩阵元素都为0

zero_matrix = np.zeros_like(one_matrix)

zero_matrix

效果：

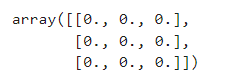
从现有数据生成数组，通过np.array(object, dtype)或np.asarray(a, dtype)

arr = np.array([[3, 4],[1, 2]])

print([[3, 4],[1, 2]])

arr

效果：

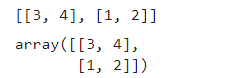
arr1 = np.array(arr)

arr1

效果：

arr2 = np.asarray(arr)

arr2

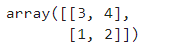
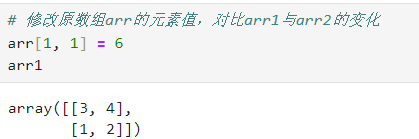
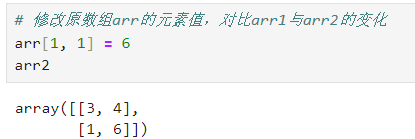
可以发现，arr1和arr2与arr1完全一直，但是采用了不同的函数，实际上这两个复制函数是不同的，对于arr1采用的是np.array()，而arr2采用的是np.asarray()。当修改arr的元素值时候，arr1的元素值不会改变，而arr2的元素值会随着arr的元素值的改变而改变，示例如下：

# 修改原数组arr的元素值，对比arr1与arr2的变化

arr[1, 1] = 6

生成固定范围的数组，利用np.arange()

通过np.linspace(start,stop,num=50)、np.arange([start=None],stop=None,[stop=None])、np.logspace(start,stop,num=50)均可以生成指定范围的数字，以np.arange()示例如下：

arr = np.arange(0, 13, 2)

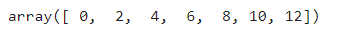
可以发现生成的数组不包含指定的最后一个数字，因为这个区间设定是左闭右开的。

公众号：愚生浅末

4. 生成随机数组

生成随机数组有多种方法。

rand基本用法

numpy.randon.rand(d0,d1,...dn),产生[0,1)之间均匀分布的随机浮点数，其中d0,d1,...dn标识传入的数组形状。

np.random.rand(2)#产生形状为(2,)的数组，也就是相当于有两个元素的一维数组

np.random.rand(2,4)#产生一个形状为(2,4)的数组，数组中的每个元素是[0,1)之间均匀分布的随机浮点数

random基本用法

numpy.random.random(size),产生[0,1)之间的随机浮点数，非均匀分布

numpy.random.random_sample、numpy.random.ranf、numpy.random.sample用法与该函数类似

注意：该函数和rand()的区别

(1)random()参数只有一个参数"size",有3种取值：None,int型整数,int型元组。而在之前的numpy.random.rand()中可以有多个参数。例如，如果要产生一个3*3的随机数组（不考虑服从什么分布)，那么在rand()中的写法是：numpy.random.rand(3,3),而在random中的写法是numpy.random.random((3,3)),这里面是个元组，是有小括弧的。

(2)random()产生的随机数的分布为非均匀分布，numpy.random.rand()产生的随机数的分布为均匀分布

#产生一个[0,1)之间的形状为(3,3)的数组

np.random().random((3,3))

#产生[-5,0)之间的形状为(3,3)的随机数组，即5*[0,1)-5

5*np.random.random_sample((3,3))-5

#产生[5,10)之间的形状为(3,3)的随机数组，即10*[0,1)-5[0,1)+5

(10-5)*np.eandom.random_sample((3,3))+5

numpy.random.uniform

np.random.uniform(0.0, 1.0,size=None),从指定范围内产生均匀分布的随机浮点数，如果在seed()中传入的数字相同，那么接下来生成的随机数序列都是相同的，仅作用于最接近的那句随机数产生语句

#默认产生一个[0,1)之间随机浮点数

np.random.uniform()

#默认产生一个[1,5)之间的形状为(2,4)的随机浮点数

np.random.uniform(1,5,size=(2,4))

randn基本用法

np.random.randn(d0,d1,...,dn),产生服从于标准正态分布（均值为0，方差为1）的随机浮点数，使用方法和rand()类似

# 产生形状为(2,)的数组

np.random.rand(2)

# 产生形状为(2,4)的数组

np.random.rand(2,4)

如果要指定正态分布的均值和方差，则可以使用这个公式：

sigma * np.random.randn(...) + mu:2.5 *np.random.randn(2,4) + 3

注意：2.5是标准差（不是方差），3是期望

normal基本用法

numpy.random.normal(loc=0.0, scale=1.0, size=None)，产生服从正态分布（均值为loc，标准差为scale）的随机浮点数

#产生均值为1标准差为10形状为(1000,)的数组

np.random.normal(1,10,100)

#产生均值为3标准差为2形状为(2,4)的数组

np.random.normal(3,2,size=(2,4))

randint基本用法

numpy.random.randint(low[,high,size,dtype]),产生[low,high)之间的随机数，如果high不知名，则产生[0,low)之间的随机整数，size可以是int整数，或者int型的元组，标识产生随机数的个数，或者随机数组的形状。dtype标识具体随机数的类型，默认是int，可以指定成int64.

#产生一个[0,10)之间的随机整数

np.random.randint(10)

#产生一个[0,10)之间的随机整数8个，以数组的形式返回

np.random.randint(10,size=8)

#产生一个[5,10)之间的形状为(2,4)的随机整数8个，以数组的形式返回

np.random.randint(5,10,size=(2,4))

choice基本用法

numpy.random.choice(a, size=None, replace=True, p=None),从一维arrary a中按概率p选择size个数组，若a为int，则从np.arrange(a)中选择，若a为array，则直接从a中选择。

numpy.random.choice(5,3)#从np.arrange(a)中等概率选择3个，等价于np.random.randint(0,5,3)

numpy.random.choice(5,3,p=[0.1,0,0.3,0.6,0])#从np.arrange(a)中按概率p选择3个

numpy.random.choice(5,3,p=[0.1,0,0.3,0.6,0]

numpy.random.choice(5,3,replace=False,p=[0.1,0,0.3,0.6,0])

aa_milne_arr = ['pooh','rabbit','piglet','Christopher']

np.random.choice(aa_milne_arr,5,p=[0.5,0.1,0.1,0.3])

numpy.random.shuffle

numpy.random.shuffle(x)按x的第一个维度进行打乱，x只能是array

np.random.shuffle(np.arange(9).reshape((3,3)))#对np.arange(9).reshape((3,3))打乱

numpy.random.permutation

numpy.random.permutation(x),按x的第一个维度进行打乱，若a为int，则对np.arrange(a)打乱，若a为array,则直接对a打乱

np.random.permutation(10)#对np.arange(10)打乱

np.random.permutation(np.arange(9).reshape((3,3)))#对np.arange(9).reshape((3,3))打乱

numpy.random.seed

若果在seed()中传入的数字相同，那么接下来生成的随机数序列都是相同的，仅作用于最接近的那句随机数产生语句

np.random.seed(10)

temp1 = np.random.rand(4)

np.random.seed(10)

temp2=np.random.rand(4)

temp3=np.random.rand(4)

上述temp1和temp2是相同的，temp3是不同的，因为seed仅作用于最接近的那句随机数产生语句。

numpy.linspace

numpy.linspace(start,stop,num=50,endpoint = True,retstep = False,dtype = None,axis = 0),区间均等分

np.linspace(2.0,3.0,num=5) #array([2.,2.25,2.5,2.75,3.])

np.linspace(2.0,3.0,num=5,endpoint=False) #array([2.,2.2,2.4,2.6,2.8])

np.linspace(2.0,3.0,num=5,retstep=True) #(array([2.,2.25,2.5,2.75,3.]),0.25)

zeros(),ones(),empty(),eye(),identity(),diag()

zeros(),ones(),empty()三者用法一样，np.zeros(3,dtype=int) np.zeros((2,3))
使用empty()时需要对生成的每一个数进行重新赋值，否则即为随机数，所以慎重使用
np.eye(2,3,k=1)he np.identity(3) : np.identity只能创建方形矩阵，np.eye可以创建矩形矩阵，且k值可以调节，为1 的对角线的位置偏离度，0居中，1向上偏离1,2向上偏离2，以此类推，-1向下偏离。值的绝对值过大就偏离出去了，整个矩阵就全是0了。np.diag可以创建对角矩阵。

数组的索引、切片

ndarray的索引、切片与list稍不同，他只有一个'[]'代码如下：

arr = np.array([ [[1, 2, 3],[4, 5, 6]], [[7, 8, 9],[10, 11, 12]] ])

list1 = [ [[1, 2, 3],[4, 5, 6]], [[7, 8, 9],[10, 11, 12]] ]

# 以下两种方法取值相同

a1 = arr[0, :]

b1 = arr[0][:]

print(list1[0][:])  # list只能用两个中括号来取值

print(a1, b1) # [[1, 2, 3][4, 5, 6]]

a2 = arr[0, 0, 0]

print(a2) # 1

可以看到ndarray的切片索引方法就是：对象[x, y, z, …]先行后列,依据对象的纬度输入的参数也不同。对于ndarray来说，以下两种索引方式均可以。

a = [[1, 2, 3],[4, 5, 6]], [[7, 8, 9],[10, 11, 12]]

b = np.array(a)

print(b[0, 1])  # array([4, 5, 6])

print(b[0][1])  # array([4, 5, 6])

而对于二维的list而言，只能使用[][][] []索引

a = [[1, 2, 3],[4, 5, 6]], [[7, 8, 9],[10, 11, 12]]

# b = np.array(a)

# print(a[0, 1]), 该种索引方式会报错

print(a[0][1])  # [4, 5, 6]

形状修改

通过ndarray.T可以实现一个矩阵的转置，代码如下：

arr = np.array([[1, 2],[3, 4]])

arr.T  # [[1, 3],[2, 4]]

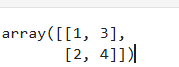
可以通过ndarray.reshapre()将arr变成一个1行4列的数组，reshape()实际上是将原来的数组压平成一维数组，然后再重新排序成目标形状，但不改变原数组。代码如下：

new_arr = arr.reshape([1, 4])

new_arr  # [[1, 2, 3, 4]]

也可以通过ndarray.resize()实现改变结构，但是resize()会改变原数组，而不是直接返回一个新数组。代码如下：

arr.resize([1, 4])

arr  # [[1, 2, 3, 4]]

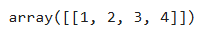
通过np.repeat(a,reps,axis)，可以实现对原数组的复制、重构。其中a是目标数组，reps是重复的次数，axis标识沿某个方向复制。若axis=0，则沿第0个维度变化的方向复制，即增加了行数，若axis=None，则原数组会展平成一维数组，代码如下：

arr = np.array([[1, 2], [3, 4]])

flat_arr = np.repeat(arr, 2)

flat_arr  # [1, 1, 2, 2, 3, 3, 4, 4]

re_arr = np.repeat(arr, 2, axis = 1)

re_arr  # [[1, 1, 2, 2], [3, 3, 4, 4]]

通过np.tile(a, reps)，以可以实现对通过复制原数组构建新的数组，其中a是目标数组，reps是重复的次数。相较于np.repeat()，np.tile()的参数更少，但而这实现的功能是类似的，但其复制的规则不同，np.tile()是对整个array进行复制，np.repeat()是对其中的元素进行复制代码如下：

arr = np.array([[1, 2], [3, 4]])

flat_arr = np.tile(arr, 2)

flat_arr  # [1, 1, 2, 2, 3, 3, 4, 4]

tile_arr = np.tile(arr, (2, 1))

tile_arr  # [[1, 2], [3, 4], [1, 2], [3, 4]]

通过np.concatenate((a, b), axis)可以实现对数组的连接,其中a、b分别标识两个数组；axis表示沿着第几个维度叠加，例如，axis=0时，即沿第0个维度变化的方向相加，代码如下：

a = [[1, 2], [3, 4]]

b = [[10, 11], [12, 13]]

res1 = np.concatenate((a, b), axis = 0)

res1  # [[1, 2], [3, 4], [10, 11], [12, 13]]

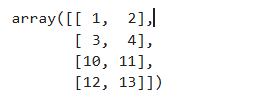
res2 = np.concatenate((a, b), axis = 1)

res2  # [[1, 2, 10, 11], [3, 4, 12, 13]]

此外，np.vstack((a, b))的作用与np.concatenate((a, b), axis = 0)相似，np.hstack((a, b))的作用与np.concatenate((a, b), axis = 1)相似,代码如下：

v_res = np.vstack((a, b))

v_res  # [[1, 2], [3, 4], [10, 11], [12, 13]]

h_res = np.hstack((a, b))

h_res  # [[1, 2, 10, 11], [3, 4, 12, 13]

类型修改

首先生成一个数组，代码如下：

# 生成数组

arr = np.array([[1, 2], [3, 4]])

可以通过ndarray.astype(str)将这个数组中的每个元素都变成string类型，该方法不改变原数组，而是返回一个新数组，代码如下：

arr1 = arr.astype(str)

arr1  # [['1' '2'], ['3' '4']]

数组的通用函数

通过np.unique()可以实现对一个现有数组，除去其中重复的元素，返回一个没有重复元素的一维数组，且这个方法不会改变原数组，代码如下：

arr = np.array([[1, 1, 2, 3],[1, 22, 34, 5]])

unique = np.unique(arr)

unique  # [1, 2, 3, 5, 22, 34]

如果按某个维度去重，则使用axis指定去重维度即可，代码如下：

a = [[1, 2, 3],[4, 5, 6]], [[1, 2, 3],[4, 5, 6]]

b = np.array(a)

c = np.unique(b, axis=0)

print(c)  # array([[[1, 2, 3], [4, 5, 6]]])

通过np.intersect1d()和np.union1d()，可以分别实现求两个矩阵的交集和并集。代码如下：

a = [1, 2, 3, 4]

b = [3, 4, 5, 6]

print(np.intersect1d(a, b))  # [3, 4]

print(np.union1d(a, b))  # [1, 2, 3, 4, 5, 6]

Numpy中还有一些常用的一元函数、二元函数，在原数组进行操作，直接修改原数组的元素。np.abs()，可以实现计算浮点数、整数或复数的绝对值.

a = [-1, 2, -3, 4]

print(np.abs(a))  # [1, 2, 3, 4]

np.sqrt()，可以实现计算元素的平方根，相当于Python中的“ ** ”的反函数

b = [3, 4, 5, 6]

print(np.sqrt(b))  # [1.73205081, 2, 2.23606798, 2.44948974]

print(2**2)

np.square()计算各元素的平方，np.exp()可以计算各元素的e指数，np.power(arr, t)可以计算数组中各元素t次方

# np.square()计算各元素的平方，np.exp()可以计算各元素的e指数，np.power(arr, t)可以计算数组中各元素t次方

a = [-1, 2, -3, 4]

print(np.square(a))  # [1, 4, 9, 16]

print(np.exp(a))  # [3.67879441e-01, 7.38905610e+00, 4.97870684e-02, 5.45981500e+01]

print(np.power(a, 3)) # [ -1, 8, -27, 64]

np.isnan()用于判断数组中哪些元素是空值

c = [1, np.nan, 3, 5]

print(np.isnan(c))  # [False, True, False, False]

np.sum(np.isnan(c))

np.where()可以对数组进行筛选，有两种用法：

1、np.where(condition, x, y)：x, y是两个数组，condition指选择条件，若满足条件则输出x，否则，输出y；

2、np.where(condition)：condition是一个条件，输出数组中满足条件的下标。

a = [[1, 2], [3, 0]]

b = [[7, 8], [9, 1]]

c = [1, 2, 3, 4]

print(np.where([[True, False], [False, False]], a, b))  # [[1, 2], [9, 0]]

np.where(np.array(c)>2)

c = np.array(a)

np.where(c > 1)

输出结果：

(array([0, 1], dtype=int64), array([1, 0], dtype=int64))

Numpy也实现了三角函数的计算，np.sin()，np.cos()，np.tan()

a = [-1, 2, -3, 4]

print(np.sin(a))  # [-0.84147098, 0.90929743, -0.14112001, -0.7568025 ]

print(np.cos(a))  # [ 0.54030231, -0.41614684, -0.9899925, -0.65364362]

print(np.tan(a))  # [-1.55740772, -2.18503986, 0.14254654, 1.15782128]

线性代数

NumPy的中的np.linalg模块实现了许多矩阵的基本操作，如：求对角线元素，求对角线元素的和（求迹）、矩阵乘积、求解矩阵行列式等。

首先生成两个数组，代码如下：

# 生成两个数组

a = [1, 2, 3]

b = [[1, 3, 9], [2, 7, 0], [4, 3, 2]]

通过np.diag(matrix)，matirx为一个矩阵，当matrix为二维数组时，以一维数组的形式返回方阵的对角线；当matrix为一维数组时，则返回非对角线元素均为0的方阵。

print(np.diag(a))  # [[1, 0, 0], [0, 2, 0], [0, 0, 3]]

print(np.diag(b))  # [1, 7, 2]

通过np.trace()，可以计算矩阵对角线元素的迹

print(np.trace(b))  # 10

通过np.dot()可以实现矩阵乘积

print(np.dot(b, a))  # [34, 16, 16]

通过np.det()可以计算矩阵的行列式

np.linalg.det(b)  # -196.00000000000009

np.linalg.eig()可以计算方阵的特征值、特征向量

eig = np.linalg.eig(b)

array([-4.40641364,  9.92452468,  4.48188896])

# 特征值

eig[0]  # [-4.40641364, 9.92452468, 4.48188896]

# 特征向量

eig[1]  # [[0.86881121, -0.6982852, 0.69750503], [-0.15233731,  -0.47753756, -0.55399068], [-0.47112676, -0.53325009, 0.4545119]]

np.linalg.inv()可以计算矩阵的逆

np.linalg.inv(b)  # [[-0.07142857, -0.10714286, 0.32142857], [0.02040816, 0.17346939, -0.09183673], [0.1122449, -0.04591837, -0.00510204]]

np.linalg.solve(A，b)可以求解线性方程组Ax=b，A为一个方阵

np.linalg.solve(b,a)  # [0.67857143, 0.09183673, 0.00510204]

np.linalg.svd(a, full_matrices = 1, compute_uv = 1)可以用于矩阵的奇异值分解，返回该矩阵的左奇异值（u）、奇异值（s）、右奇异值（v）

svd = np.linalg.svd(b)

svd

统计分析

1）通过np.sum(a, axis)计算数组a沿指定轴的和；

2） np.mean(a,axis)计算数组a沿指定轴的平均值；

3） min(axis)和a.max(axis)用于获取数组a，沿指定轴的最小值和最大值；

4） np.std(a,axis)计算数组a沿指定轴的标准差；

5） np.var(a,axis)计算数组a沿指定轴的方差；

6） np.argmin(a,axis)和np.argmax(a,axis)分别用于获取数组a，沿指定轴的最小值和最大值的索引。

注：axis=None时，会返回所有元素的和；axis=0时，会沿着第0个维度（也就是列）的变化方向进行计算，即按列求和；axis=1时，则为按行求和，以此类推。

a = np.array([[1, 2, 3], [4, 5, 6]])

# 通过np.sum(a, axis)计算数组a沿指定轴的和

print(np.sum(a))  # 21

print(np.sum(a, axis=0))  # [5, 7, 9]

#  np.mean(a,axis)计算数组a沿指定轴的平均值

print(np.mean(a, axis=1))  # [2, 5]

# min(axis)和a.max(axis)用于获取数组a，沿指定轴的最小值和最大值

print(a.min(axis=0))  # [1, 2, 3]

#  np.std(a,axis)计算数组a沿指定轴的标准差

print(np.std(a, axis=1))  # [0.81649658, 0.81649658]

#  np.argmin(a,axis)和np.argmax(a,axis)分别用于获取数组a，沿指定轴的最小值和最大值的索引

print(np.argmax(a, axis=1))  # [2, 2]

公众号：愚生浅末

欢迎关注公众号：愚生浅末

公众号本文地址：https://mp.weixin.qq.com/s/EocThNWhQlI2zeLcUApsQQ