POJ1759 Garland —— 二分

题目链接：http://poj.org/problem?id=1759

Garland

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 2477		Accepted: 1054

Description

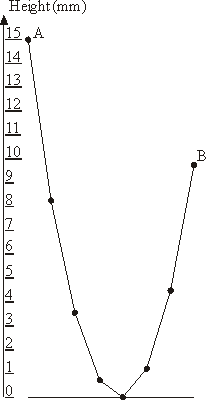The New Year garland consists of N lamps attached to a common wire that hangs down on the ends to which outermost lamps are affixed. The wire sags under the weight of lamp in a particular way: each lamp is hanging at the height that is 1 millimeter lower than the average height of the two adjacent lamps.

The leftmost lamp in hanging at the height of A millimeters above the ground. You have to determine the lowest height B of the rightmost lamp so that no lamp in the garland lies on the ground though some of them may touch the ground.

You shall neglect the lamp's size in this problem. By numbering the lamps with integers from 1 to N and denoting the ith lamp height in millimeters as Hi we derive the following equations:

H1 = A 
Hi = (H_i-1 + H_i+1)/2 - 1, for all 1 < i < N 
HN = B 
Hi >= 0, for all 1 <= i <= N

The sample garland with 8 lamps that is shown on the picture has A = 15 and B = 9.75.

Input

The input file consists of a single line with two numbers N and A separated by a space. N (3 <= N <= 1000) is an integer representing the number of lamps in the garland, A (10 <= A <= 1000) is a real number representing the height of the leftmost lamp above the ground in millimeters.

Output

Write to the output file the single real number B accurate to two digits to the right of the decimal point representing the lowest possible height of the rightmost lamp.

Sample Input

692 532.81

Sample Output

446113.34

Source

Northeastern Europe 2000

 

 

 

 

题解：

　　错误思路：惯性思维，一上来就想二分答案，即B点。但问题是，知道了A、B点，怎么求出中间的点呢？首先递推是推不出来的，然后就尝试用递归，看能否“先前进再返回”地求出各点，结果还是不行。后来也大概得出结论，如果要求出各个点：1)要么能推导出关于A、B点的公式直接计算；2)要么是知道相邻两个点的值，然后一路递推。公式我是推导不出来的，所以就要尝试第二种方法。所以：

1.二分第二个点，然后一路递推，直到求出B。

2.根据：H[i] = 2*H[i-1] + 2 - H[i-2] 可知，当H[i-2]固定时（对应A点已知），H[i-1]越小（对应第二个点） H[i]的值也越小。然后一直递推，最终B的值也越小。所以二分的第二个点B点具有同增同减性。

　　　—— 然而这个证明很牵强，因为H[i+1]越小时，应该是H[i]尽可能小， H[i-1]尽可能大。但此时H[i]、H[i-1]都是尽可能小，所以并不能说明：在第二个点越小的情况下，H[i+1]也越小，同理B点。所以也无法说明第二个点与B点具有同增同减性，那怎么证明呢？如下：

可知：H[3] = 2*H[2] + 2 - H[1] 

那么：H[4] = 2*H[3] + 2 - H[2]

得出：H[4] = 3*H[2] +6 - 2*H[1]。

一直将H[i]的式子带入H[i+1]的式子，那么得到：H[i+1] = a*H[2] + b - c*H[1]， 其中a和b和c为正数。所以H[i+1]的增减性就显而易见了，因为H[1]已经确定，根据一元一方方程的特性，H[2]（二分的第二个点）的值越小， H[i+1]的值也越小。所以表明了第二个点与所有点具有相同的增减性。所以，第二个点的值越小，B的值也越小。

　　—— 或者，还有一个更快“目测”方法。观察：H[i] = 2*H[i-1] + 2 - H[i-2] 。 H[i-1] 的系数为2， H[i-2]的系数为1，所以H[i-1]占H[i]的权重最大，所以就可以得出：H[i] 与 H[i-1] 同增同减，一路递推。所以第二个点与B点具有同增同减性。

 

 

 

 

代码如下：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <cmath>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 #define rep(i,a,n) for(int (i) = a; (i)<=(n); (i)++)
 #define ms(a,b) memset((a),(b),sizeof((a)))
 using namespace std;
 typedef long long LL;
 const double EPS = 1e-;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const int mod = 1e9+;
 const int maxn = 1e5+;

 int n;
 double A, ans;

 bool test(double x1, double x2)
 {
     for(int i = ; i<=n; i++)   //递推出每个点的高度
     {
         double x3 = *x2+-x1;
         if(x3<=) return false; //出现负数，证明接地了， 不符合。
         x1 = x2, x2 = x3;
     }
     ans = x2;   //符合条件， 则更新答案。
     return true;
 }

 int main()
 {
     while(scanf("%d%lf", &n, &A)!=EOF)
     {
         double l = , r = A;    //二分第二个点
         while(l+EPS<=r)
         {
             double mid = (l+r)/;
             if(test(A, mid))
                 r = mid - EPS;
             else
                 l = mid + EPS;
         }
         printf("%.2f\n", ans);
     }
 }