luogu P1775 古代人的难题_NOI导刊2010提高（02）（斐波纳契+数学）

题意

已知x，y为整数，且满足以下两个条件：

1．x，y∈[1…k]，且x，y，k∈Z

2.（x^2-xy-y^2）^2=1

给你一个整数k，求一组满足上述条件的x，y并且使得x^2+y^2的值最大。

k<=10¹⁸

题解

这题需要推式子

(x²-xy-y²)²=1

(y²+xy-x²)²=1

[(x+y)²-xy-2x²)]²=1

[(x+y)²-(x+y)x-x²)]²=1

然后因为斐波那契数列有一个性质：

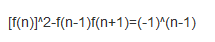
把f[n+1]变成f[n]+f[n-1]这个式子就变成了：

f[n]²-f[n]f[n-1]-f[n-1]²=(-1)^n-1

发现这两个式子很像

仔细观察我们发现，当x+y=f[n],x=f[n-1]时式子成立

令x1=x+y;y1=x;

(x1²-x1y1-y1²)²=1即当x1=f[n],y1=f[n-1]时式子成立

我们要求x²+y²的最大值。

就是求f[n]²+f[n-1]²的最大值。

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #include<algorithm>
 using namespace std;
 unsigned long long n,f[];
 int now;
 int main(){
     scanf("%llu",&n);
     now=;
     f[]=;f[]=;f[]=;
     while(n>=f[now]){
         now++;
         f[now]=f[now-]+f[now-];
     }
     printf("%llu %llu",f[now-],f[now-]);
     return ;
 }