ATcoder 1983 BBQ Hard

E - BBQ Hard

---

Time limit : 2sec / Memory limit : 256MB

Score : 1400 points

Problem Statement

Snuke is having another barbeque party.

This time, he will make one serving of Skewer Meal.

He has a stock of N Skewer Meal Packs. The i-th Skewer Meal Pack contains one skewer, Ai pieces of beef and Bi pieces of green pepper. All skewers in these packs are different and distinguishable, while all pieces of beef and all pieces of green pepper are, respectively, indistinguishable.

To make a Skewer Meal, he chooses two of his Skewer Meal Packs, and takes out all of the contents from the chosen packs, that is, two skewers and some pieces of beef or green pepper. (Remaining Skewer Meal Packs will not be used.) Then, all those pieces of food are threaded onto both skewers, one by one, in any order.

(See the image in the Sample section for better understanding.)

In how many different ways can he make a Skewer Meal? Two ways of making a Skewer Meal is different if and only if the sets of the used skewers are different, or the orders of the pieces of food are different. Since this number can be extremely large, find it modulo 109+7.

Constraints

• 2≦N≦200,000
• 1≦Ai≦2000,1≦Bi≦2000

---

Input

The input is given from Standard Input in the following format:

N
A1 B1
A2 B2
:
AN BN

Output

Print the number of the different ways Snuke can make a serving of Skewer Meal, modulo 109+7.

---

Sample Input 1

3
1 1
1 1
2 1

Sample Output 1

26

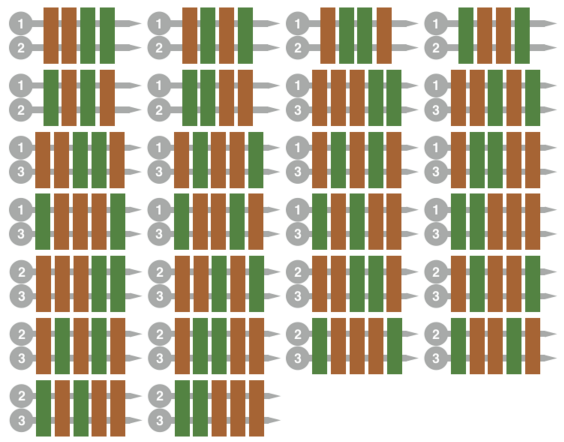
The 26 ways of making a Skewer Meal are shown below. Gray bars represent skewers, each with a number denoting the Skewer Meal Set that contained the skewer. Brown and green rectangles represent pieces of beef and green pepper, respectively.

 

 

 

我们可以先强行把 有序对转化成无序对并可以自己加自己的形式，也就是题目要求的 Σ(i=1 to n)Σ(j=i+1 to n) C(a[i]+a[j]+b[i]+b[j] , a[i]+a[j])=[ Σ(i=1 to n)Σ(j=1 to n) C(a[i]+a[j]+b[i]+b[j] , a[i]+a[j])  - Σ(i= 1 to n) C(a[i]*2+b[i]*2 , a[i]*2) ]/2。

后面那个Σ好求，直接带一遍组合数就行了，所以现在问题的关键是Σ(i=1 to n)Σ(j=1 to n) C(a[i]+a[j]+b[i]+b[j] , a[i]+a[j]) 怎么求。

考虑到a[],b[]都是<=2000的，可以从这里入手。我们发现，设点X[i] = {-a[i] , -b[i]} ,Y[i] = {a[i] , b[i]} ，那么上式的含义就是在二维平面上，每次只能向右或者向上走，从每个X[i] 走到每个Y[j]的方案数的和，而这个玩意又很好dp，嗯。。。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int ha=1000000007;
const int maxn=4005;
const int N=200005,inv=ha/2+1;
int n,px[N],py[N],jc[maxn<<1];
int ans=0,f[maxn][maxn],ni[maxn<<1];

inline int add(int x,int y){
	x+=y;
	return x>=ha?x-ha:x;
}

inline int ksm(int x,int y){
	int an=1;
	for(;y;y>>=1,x=x*(ll)x%ha) if(y&1) an=an*(ll)x%ha;
	return an;
}

inline void init(){
	jc[0]=1;
	for(int i=1;i<=8000;i++) jc[i]=jc[i-1]*(ll)i%ha;
	ni[8000]=ksm(jc[8000],ha-2);
	for(int i=8000;i;i--) ni[i-1]=ni[i]*(ll)i%ha;
}

inline void dp(){
	for(int i=0;i<=4000;i++)
	    for(int j=0;j<=4000;j++){
	    	if(i) f[i][j]=add(f[i][j],f[i-1][j]);
	    	if(j) f[i][j]=add(f[i][j],f[i][j-1]);
		}
}

inline int C(int x,int y){
	return jc[x]*(ll)ni[y]%ha*(ll)ni[x-y]%ha;
}

inline void calc(){
	for(int i=1;i<=n;i++) ans=add(ans,f[2000+px[i]][2000+py[i]]);
	for(int i=1;i<=n;i++) ans=add(ans,ha-C((px[i]+py[i])<<1,py[i]<<1));
	ans=ans*(ll)inv%ha;
}

int main(){
	init();
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d%d",px+i,py+i);
		f[2000-px[i]][2000-py[i]]++;
	}
	dp();
	calc();
	printf("%d\n",ans);
	return 0;
}