Codeforces Round #470 Div. 2题解

A. Protect Sheep

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Bob is a farmer. He has a large pasture with many sheep. Recently, he has lost some of them due to wolf attacks. He thus decided to place some shepherd dogs in such a way that all his sheep are protected.

The pasture is a rectangle consisting of R × C cells. Each cell is either empty, contains a sheep, a wolf or a dog. Sheep and dogs always stay in place, but wolves can roam freely around the pasture, by repeatedly moving to the left, right, up or down to a neighboring cell. When a wolf enters a cell with a sheep, it consumes it. However, no wolf can enter a cell with a dog.

Initially there are no dogs. Place dogs onto the pasture in such a way that no wolf can reach any sheep, or determine that it is impossible. Note that since you have many dogs, you do not need to minimize their number.

Input

First line contains two integers R (1 ≤ R ≤ 500) and C (1 ≤ C ≤ 500), denoting the number of rows and the numbers of columns respectively.

Each of the following R lines is a string consisting of exactly C characters, representing one row of the pasture. Here, 'S' means a sheep, 'W' a wolf and '.' an empty cell.

Output

If it is impossible to protect all sheep, output a single line with the word "No".

Otherwise, output a line with the word "Yes". Then print R lines, representing the pasture after placing dogs. Again, 'S' means a sheep, 'W' a wolf, 'D' is a dog and '.' an empty space. You are not allowed to move, remove or add a sheep or a wolf.

If there are multiple solutions, you may print any of them. You don't have to minimize the number of dogs.

Examples

input

Copy

6 6
..S...
..S.W.
.S....
..W...
...W..
......

output

Yes
..SD..
..SDW.
.SD...
.DW...
DD.W..
......

input

Copy

1 2
SW

output

No

input

Copy

5 5
.S...
...S.
S....
...S.
.S...

output

Yes
.S...
...S.
S.D..
...S.
.S...

Note

In the first example, we can split the pasture into two halves, one containing wolves and one containing sheep. Note that the sheep at (2,1) is safe, as wolves cannot move diagonally.

In the second example, there are no empty spots to put dogs that would guard the lone sheep.

In the third example, there are no wolves, so the task is very easy. We put a dog in the center to observe the peacefulness of the meadow, but the solution would be correct even without him.

题意：给定一个$R\times C$的草坪，草坪上有一些羊和一些狼，你可以在羊的周围放一些狗，有狗的地方狼就过不去了，问是否存在一种方案使得所有的羊都能不被吃掉，并输出任意一组解。

题解：随便输出一组解的话，我们可以贪心地思考，把每一块空地都放一只狗，然后以每一只狼为起点进行一遍DFS，如果能碰到羊就无解，如果到最后都没有羊被吃掉，那么就输出方案。

#include<cstdio>
#include<cstring>
#include<cstdlib>
using namespace std;
char a[510][510];
bool vis[510][510];
int r,c;
const int dx[]={-1,1,0,0},dy[]={0,0,1,-1};
void dfs(int x,int y)
{
	if(a[x][y]=='S')
	{
		puts("No");
		exit(0);
	}
	int xx,yy;
	for(int i=0;i<4;i++)
	{
		xx=x+dx[i],yy=y+dy[i];
		if(xx>=0&&yy>=0&&xx<r&&yy<c&&a[xx][yy]!='D')
		{
			if(!vis[xx][yy])
			{
				vis[xx][yy]=1;
				dfs(xx,yy);
			}
		}
	}
}
int main()
{
	scanf("%d%d",&r,&c);
	for(int i=0;i<r;i++)
		scanf("%s",a[i]);
	for(int i=0;i<r;i++)
		for(int j=0;j<c;j++)
			if(a[i][j]=='.')
				a[i][j]='D';
	for(int i=0;i<r;i++)
		for(int j=0;j<c;j++)
			if(a[i][j]=='W')
				dfs(i,j);
	puts("Yes");
	for(int i=0;i<r;i++)
		printf("%s\n",a[i]);
	return 0;
}

这么水的题竟然写了接近50行qwq。。。

B. Primal Sport

time limit per test

1.5 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Alice and Bob begin their day with a quick game. They first choose a starting number X0 ≥ 3 and try to reach one million by the process described below.

Alice goes first and then they take alternating turns. In the i-th turn, the player whose turn it is selects a prime number smaller than the current number, and announces the smallest multiple of this prime number that is not smaller than the current number.

Formally, he or she selects a prime p < Xi - 1 and then finds the minimum Xi ≥ Xi - 1 such that p divides Xi. Note that if the selected prime p already divides Xi - 1, then the number does not change.

Eve has witnessed the state of the game after two turns. Given X2, help her determine what is the smallest possible starting number X0. Note that the players don't necessarily play optimally. You should consider all possible game evolutions.

Input

The input contains a single integer X2 (4 ≤ X2 ≤ 106). It is guaranteed that the integer X2 is composite, that is, is not prime.

Output

Output a single integer — the minimum possible X0.

Examples

input

Copy

14

output

6

input

Copy

20

output

15

input

Copy

8192

output

8191

Note

In the first test, the smallest possible starting number is X0 = 6. One possible course of the game is as follows:

• Alice picks prime 5 and announces X1 = 10
• Bob picks prime 7 and announces X2 = 14.

In the second case, let X0 = 15.

• Alice picks prime 2 and announces X1 = 16
• Bob picks prime 5 and announces X2 = 20.

题意：两个人玩游戏，先指定一个$X_0$，第$i$轮的时候他会选择一个满足$p\le X_i$的质数，然后找到一个最小的数满足$X_{i+1}>X_i,X_{i+1}\mid p$，如此进行若干轮。现在给定你$X_2$，你要求出最小的$X_0$。

题解：令$P(N)$为$N$的最大质因数，显然我们可以通过选择$P(N)$作为每次操作的质数获得区间$[N-P(N)+1,N]$中的任意数，并且我们不能从其他任何数获得$N$。通过分解$X_2$，我们可以找到$X_1$的区间，通过分解$X_1$区间中的所有数，我们可以找到$X_0$的区间，答案是$X_1$区间交集的最小元素。

C. Producing Snow

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Alice likes snow a lot! Unfortunately, this year's winter is already over, and she can't expect to have any more of it. Bob has thus bought her a gift — a large snow maker. He plans to make some amount of snow every day. On day i he will make a pile of snow of volume Viand put it in her garden.

Each day, every pile will shrink a little due to melting. More precisely, when the temperature on a given day is Ti, each pile will reduce its volume by Ti. If this would reduce the volume of a pile to or below zero, it disappears forever. All snow piles are independent of each other.

Note that the pile made on day i already loses part of its volume on the same day. In an extreme case, this may mean that there are no piles left at the end of a particular day.

You are given the initial pile sizes and the temperature on each day. Determine the total volume of snow melted on each day.

Input

The first line contains a single integer N (1 ≤ N ≤ 105) — the number of days.

The second line contains N integers V1, V2, ..., VN (0 ≤ Vi ≤ 109), where Vi is the initial size of a snow pile made on the day i.

The third line contains N integers T1, T2, ..., TN (0 ≤ Ti ≤ 109), where Ti is the temperature on the day i.

Output

Output a single line with N integers, where the i-th integer represents the total volume of snow melted on day i.

Examples

input

Copy

3
10 10 5
5 7 2

output

5 12 4

input

Copy

5
30 25 20 15 10
9 10 12 4 13

output

9 20 35 11 25

Note

In the first sample, Bob first makes a snow pile of volume 10, which melts to the size of 5 on the same day. On the second day, he makes another pile of size 10. Since it is a bit warmer than the day before, the first pile disappears completely while the second pile shrinks to 3. At the end of the second day, he has only a single pile of size 3. On the third day he makes a smaller pile than usual, but as the temperature dropped too, both piles survive till the end of the day.

题意：有$N$堆雪，每堆雪都有一定体积，第$i$天每堆雪的体积都会缩小$T[i]$，求$1$到$N$天融化的雪的体积。

题解：由于$T[i]$是固定的，我们只需要确定每堆雪融化完的时间即可。对每堆雪的融化量做一个前缀和，然后就可以维护每天化了多少雪了。对于每堆雪的融化完成时间，直接在做前缀和的过程中就能处理完。

C. Perfect Security

time limit per test

3.5 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

Alice has a very important message M consisting of some non-negative integers that she wants to keep secret from Eve. Alice knows that the only theoretically secure cipher is one-time pad. Alice generates a random key K of the length equal to the message's length. Alice computes the bitwise xor of each element of the message and the key (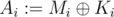, where  denotes the bitwise XOR operation) and stores this encrypted message A. Alice is smart. Be like Alice.

For example, Alice may have wanted to store a message M = (0, 15, 9, 18). She generated a key K = (16, 7, 6, 3). The encrypted message is thus A = (16, 8, 15, 17).

Alice realised that she cannot store the key with the encrypted message. Alice sent her key K to Bob and deleted her own copy. Alice is smart. Really, be like Alice.

Bob realised that the encrypted message is only secure as long as the key is secret. Bob thus randomly permuted the key before storing it. Bob thinks that this way, even if Eve gets both the encrypted message and the key, she will not be able to read the message. Bob is not smart. Don't be like Bob.

In the above example, Bob may have, for instance, selected a permutation (3, 4, 1, 2) and stored the permuted key P = (6, 3, 16, 7).

One year has passed and Alice wants to decrypt her message. Only now Bob has realised that this is impossible. As he has permuted the key randomly, the message is lost forever. Did we mention that Bob isn't smart?

Bob wants to salvage at least some information from the message. Since he is not so smart, he asks for your help. You know the encrypted message A and the permuted key P. What is the lexicographically smallest message that could have resulted in the given encrypted text?

More precisely, for given A and P, find the lexicographically smallest message O, for which there exists a permutation π such that 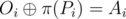 for every i.

Note that the sequence S is lexicographically smaller than the sequence T, if there is an index i such that Si < Ti and for all j < i the condition Sj = Tj holds.

Input

The first line contains a single integer N (1 ≤ N ≤ 300000), the length of the message.

The second line contains N integers A1, A2, ..., AN (0 ≤ Ai < 230) representing the encrypted message.

The third line contains N integers P1, P2, ..., PN (0 ≤ Pi < 230) representing the permuted encryption key.

Output

Output a single line with N integers, the lexicographically smallest possible message O. Note that all its elements should be non-negative.

Examples

input

Copy

3
8 4 13
17 2 7

output

10 3 28

input

Copy

5
12 7 87 22 11
18 39 9 12 16

output

0 14 69 6 44

input

Copy

10
331415699 278745619 998190004 423175621 42983144 166555524 843586353 802130100 337889448 685310951
226011312 266003835 342809544 504667531 529814910 684873393 817026985 844010788 993949858 1031395667

output

128965467 243912600 4281110 112029883 223689619 76924724 429589 119397893 613490433 362863284

Note

In the first case, the solution is (10, 3, 28), since 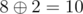,  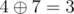and 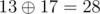. Other possible permutations of key yield messages (25, 6, 10), (25, 3, 15), (10, 21, 10), (15, 21, 15) and (15, 6, 28), which are all lexicographically larger than the solution.

题意：给定两组数，求这两组数两两异或后连接起来字典序最小的一组。

题解：我们贪心的解密每一对数，考虑要维护一些数的异或和，我们直接上Trie树把数的每一位分解，记录个数，然后在Trie树上寻找最优解即可。

D. Picking Strings

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Alice has a string consisting of characters 'A', 'B' and 'C'. Bob can use the following transitions on any substring of our string in any order any number of times:

• A  BC
• B  AC
• C  AB
• AAA  empty string

Note that a substring is one or more consecutive characters. For given queries, determine whether it is possible to obtain the target string from source.

Input

The first line contains a string S (1 ≤ |S| ≤ 105). The second line contains a string T (1 ≤ |T| ≤ 105), each of these strings consists only of uppercase English letters 'A', 'B' and 'C'.

The third line contains the number of queries Q (1 ≤ Q ≤ 105).

The following Q lines describe queries. The i-th of these lines contains four space separated integers ai, bi, ci, di. These represent the i-th query: is it possible to create T[ci..di] from S[ai..bi] by applying the above transitions finite amount of times?

Here, U[x..y] is a substring of U that begins at index x (indexed from 1) and ends at index y. In particular, U[1..|U|] is the whole string U.

It is guaranteed that 1 ≤ a ≤ b ≤ |S| and 1 ≤ c ≤ d ≤ |T|.

Output

Print a string of Q characters, where the i-th character is '1' if the answer to the i-th query is positive, and '0' otherwise.

Example

input

Copy

AABCCBAAB
ABCB
5
1 3 1 2
2 2 2 4
7 9 1 1
3 4 2 3
4 5 1 3

output

10011

Note

In the first query we can achieve the result, for instance, by using transitions .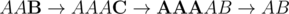

The third query asks for changing AAB to A — but in this case we are not able to get rid of the character 'B'.

题意：给两个只有$A,B,C$的字符串$S$和$T$，有$Q$次询问，每次询问能否将$S$的一段区间$[a_i,b_i]$变换为$T$的一段区间$[c_i,d_i]$。

变换方式如下：

\begin{equation*}
\begin{aligned}
A&\rightarrow BC\\
B&\rightarrow AC\\
C&\rightarrow AB\\
AAA&\rightarrow\varnothing
\end{aligned}
\end{equation*}

题解：

根据所给条件，我们对字符串进行一些变换，容易发现一些单个字符变换的规律：

\begin{equation*}
\begin{aligned}
&B\rightarrow AC\rightarrow AAB\rightarrow\mathbf{AAA}C\rightarrow C\\
&C\rightarrow AB\rightarrow AAC\rightarrow\mathbf{AAA}B\rightarrow B\\
&B\rightarrow AC\rightarrow AAB\rightarrow\mathbf{AAA}C\rightarrow\mathbf{AAA}AB\rightarrow AB\\
&C\rightarrow AB\rightarrow AAC\rightarrow\mathbf{AAA}B\rightarrow\mathbf{AAA}AC\rightarrow AC\\
&A\rightarrow BC\rightarrow BAB\rightarrow BAAC\rightarrow B\mathbf{AAA}B\rightarrow BB\\
\end{aligned}
\end{equation*}

由上述一些规律我们还容易得到：

\begin{equation*}
\begin{aligned}
&B\rightarrow AC\rightarrow AB\rightarrow BBB\\
&AAB\rightarrow \mathbf{AAA}C\rightarrow C\rightarrow B\\
&AB\rightarrow ACB\rightarrow ABB\\
\end{aligned}
\end{equation*}

综上所述，我们得到以下一些结论：

\begin{align}
&B\Leftrightarrow C\\
&B每次可以增加偶数个\\
&在B之前出现的A都可以删除\\
\end{align}

于是我们得到了原字符串和目标字符串之间的关系：

1. 目标字符串中的$B$与$C$的数量和必须大于等于原字符串中的$B$与$C$的数量和
2. 目标字符串中的$B$与$C$的数量和的奇偶性必须与原字符串中的$B$与$C$的数量和相同

最后，如果原字符串中的$B$和$C$的数量与目标字符串中的$B$和$C$的数量相等，那么没有操作$1$和操作$2$，只能将后面的$A$减少$3n,n\in N$个。由于所有操作都无法增加原字符串末尾的$A$的个数，如果原字符串末尾$A$的个数少于目标字符串就无解，否则对3取个模然后与目标字符串末尾$A$的个数对3取模的结果判一下是否相等就行了。

至于怎么维护两个字符串中$B$和$C$的数量，直接上前缀和预处理一下就行了。