直接线性变换解法（DLT）用于标定相机

直接线性变换法是建立像点坐标和相应物点物方空间坐标之间直接的线性关系的算法。特点：不需要内外方位元素；适合于非量测相机；满足中、低精度的测量任务；可以标定单个相机。

1 各坐标系之间的关系推导直接线性变换解法

1.1 像素坐标系与像平面坐标系

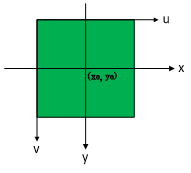
图 1 像素坐标系与像平面坐标系间的关系

两坐标系的关系式如下：

像素坐标系即CCD坐标系，是以左上角为原点，水平向右为$u$方向，竖直向下为$v$方向；像平面坐标系是影像平面内的直角坐标系，用以表示像点在像平面上的位置，其以像主点$o$为原点，$x$方向与$u$方向平行，$y$方向与$v$方向平行。其二者的关系如右图所示，

$u= \frac{x}{dx}+u_{0}\\v=\frac{y}{dy}+v_{0}$

式中，$dx$为在$x$方向上每个像素的宽度；$dy$为在$y$方向上每个像素的高度。

将上式化为齐次坐标矩阵形式为

$\begin{bmatrix}u\\ v\\ 1\end{bmatrix}=\begin{bmatrix}\frac{1}{dx} & 0 & u_{0}\\ 0 & \frac{1}{dy} & v_{0}\\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}x\\ y\\ 1\end{bmatrix}$

1.2 像平面坐标系与像空间坐标系

像空间坐标系是以摄站点$S$为坐标原点，摄影机的主光轴$SO$坐标系的$Z_{C}$轴，像空间坐标系的$X_{C}$、$Y_{C}$轴分别与像平面坐标系的$x$、$y$轴平行。

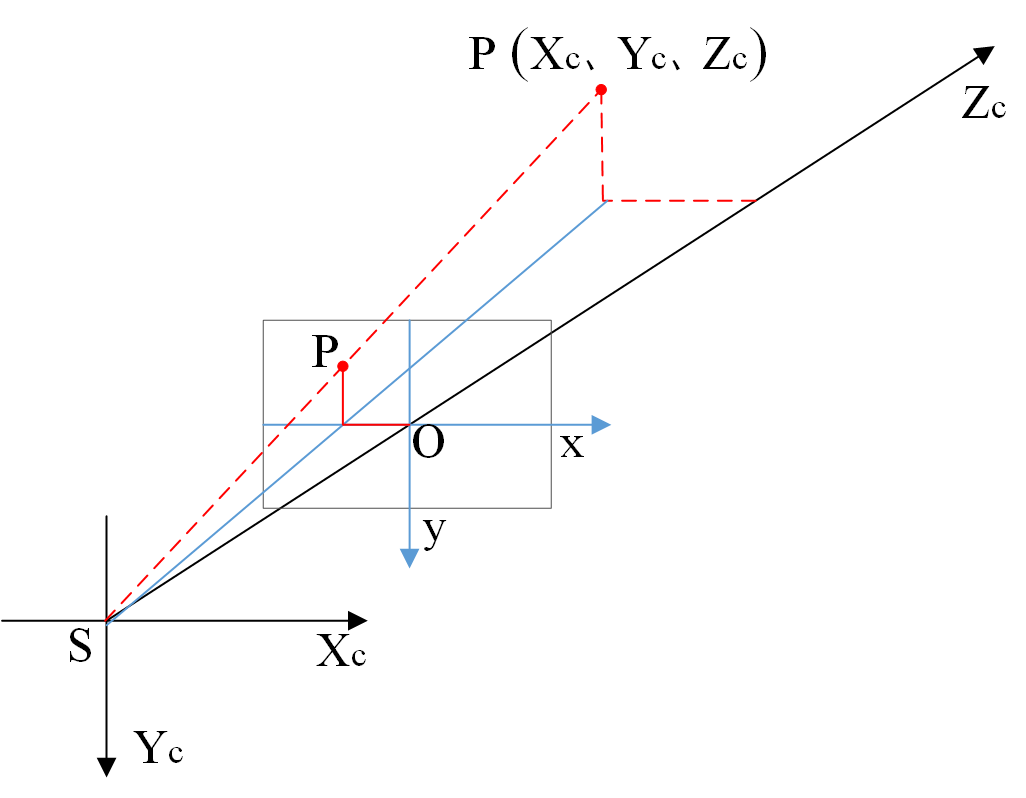
图 2 像平面坐标系与像空间坐标系的关系

两坐标系的关系如下式

$\left\{\begin{matrix}\frac{x}{f}=\frac{X_{C}}{Z_{C}}\\ \frac{y}{f}=\frac{Y_{C}}{Z_{C}}\end{matrix}\right.\Rightarrow \left\{\begin{matrix}Z_{C}\cdot x=f\cdot X_{C}\\ Z_{C}\cdot y=f\cdot Y_{C}\end{matrix}\right.$

将上式化为矩阵形式为

$Z_{C}\begin{bmatrix}x\\ y\\ 1\end{bmatrix}=\begin{bmatrix}f & 0 & 0 & 0\\ 0 & f & 0 & 0\\ 0 & 0 & 1 & 0\end{bmatrix}\begin{bmatrix}X_{C}\\ Y_{C}\\ Z_{C}\\ 1\end{bmatrix}$

1.3 像空间坐标系与笛卡尔空间坐标系

笛卡尔空间坐标系即为所摄物体所在的空间直角坐标系。两坐标系间的关系公式如下

$\begin{bmatrix}X_{C}\\ Y_{C}\\ Z_{C}\end{bmatrix}=R\begin{bmatrix}X\\ Y\\ Z\end{bmatrix}+\begin{bmatrix}X_{S}\\ Y_{S}\\ Z_{S}\end{bmatrix}$

化成齐次坐标矩阵形式为

$\begin{bmatrix}X_{C}\\ Y_{C}\\ Z_{C}\\1\end{bmatrix}=\begin{bmatrix}R & t\\ 0^{T} & 1\end{bmatrix}\begin{bmatrix}X\\ Y\\ Z\\1\end{bmatrix}=T\begin{bmatrix}X\\ Y\\ Z\\1\end{bmatrix}$

其中R，t为

$R=\begin{bmatrix}r_{11} & r_{12} & r_{13}\\ r_{21} & r_{22} & r_{23}\\ r_{31} & r_{32} & r_{33}\end{bmatrix},t=\begin{bmatrix}t_{1}\\ t_{2}\\ t_{3}\end{bmatrix}$

1.4 四种坐标系的合成

由上述四个坐标系间的转换可得像素坐标系和笛卡尔空间坐标系的转换关系，见下式

$Z_{C}\begin{bmatrix}u\\ v\\ 1\end{bmatrix}=\begin{bmatrix}\frac{1}{dx} & 0 & u_{0}\\ 0 & \frac{1}{dy} & v_{0}\\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}f & 0 & 0 & 0\\ 0 & f & 0 & 0\\ 0 & 0 & 1 & 0\end{bmatrix}\begin{bmatrix}R & t\\ 0^{T} & 1\end{bmatrix}\begin{bmatrix}X\\ Y\\ Z\\1\end{bmatrix}=\begin{bmatrix}l_{1} & l_{2} & l_{3} & l_{4}\\ l_{5} & l_{6} & l_{7} & l_{8}\\ l_{9} & l_{10} &  l_{11}& l_{12}\end{bmatrix}\begin{bmatrix}X\\ Y\\ Z\\1\end{bmatrix}$

由上式可得

$\left\{\begin{matrix}u=(l_{1}X+l_{2}Y+l_{3}Z+l_{4})/Z_{C}\\ v=(l_{5}X+l_{6}Y+l_{7}Z+l_{8})/Z_{C}\\ Z_{C}=l_{9}X+l_{10}Y+l_{11}Z+l_{12}\end{matrix}\right.\Rightarrow \left\{\begin{matrix}u=\frac{l_{1}X+l_{2}Y+l_{3}Z+l_{4}}{l_{9}X+l_{10}Y+l_{11}Z+1}\\ v=\frac{l_{5}X+l_{6}Y+l_{7}Z+l_{8}}{l_{9}X+l_{10}Y+l_{11}Z+1}\end{matrix}\right.$

$\left\{\begin{matrix}l_{1}=\frac{f\cdot r_{11}}{dx}+u_{0}\cdot r_{31} & l_{2}= \frac{f\cdot r_{12}}{dx}+u_{0}\cdot r_{32}& l_{3}= \frac{f\cdot r_{13}}{dx}+u_{0}\cdot r_{33}& l_{4}=\frac{f\cdot t_{1}}{dx}+u_{0}\cdot t_{3}\\ l_{5}= \frac{f\cdot r_{21}}{dx}+v_{0}\cdot r_{31}& l_{6}= \frac{f\cdot r_{22}}{dx}+v_{0}\cdot r_{32}& l_{7}= \frac{f\cdot r_{23}}{dx}+v_{0}\cdot r_{33}& l_{8}=\frac{f\cdot t_{2}}{dx}+v_{0}\cdot t_{3}\\ l_{9}= r_{31}& l_{10}= r_{32}& l_{11}= r_{33}& l_{12}=t_{3}\end{matrix}\right.$

式中，$(X、Y、Z)$为笛卡尔空间坐标系中的三维坐标，$(u,v)$为图像上对应三维点的像素坐标，$l_{1}...l_{12}$为笛卡尔空间坐标系与像素坐标系之间的关系系数，此外令$l_{12}=1$，因为$l_{12}$的取值对其他参数的值没有影响，顾上述两式是等同的，可由后续的计算过程证明。

2 相机内参数计算

2.1 DLT求解

将1.4小节中的最后一个方程组进行变换可得到下列等式

$\begin{bmatrix}X & Y & Z & 1 & 0 & 0 & 0 & 0 & -Xu & -Yu & -Zu\\ 0 & 0 & 0 & 0 & X & Y & Z & 1 & -Xv & -Yv & -Zv \end{bmatrix}\begin{bmatrix}l_{1}\\ l_{2}\\ l_{3}\\ l_{4}\\ l_{5}\\ l_{6}\\ l_{7}\\ l_{8}\\ l_{9}\\ l_{10}\\ l_{11} \end{bmatrix}-\begin{bmatrix}u\\ v\end{bmatrix}=0\Rightarrow BL=C$

上式中有11个未知数，每对点（像素与对应的三维点）可列两个等式，所以最少需要6对点才可解该方程。

未知数矩阵的解为

$L=(B^{T}B)^{-1}(B^{T}C)$

到此，即解出了$l_{1}...l_{11}$的值。

2.2 内参数计算

通过旋转矩阵的特性可求得相机的内参数

$\left\{\begin{matrix}u_{0}=l_{1}l_{9}+l_{2}l_{10}+l_{3}l_{11}\\ v_{0}=l_{5}l_{9}+l_{6}l_{10}+l_{7}l_{11}\\ f_{u}=\sqrt{l_{1}^{2}+l_{2}^{2}+l_{3}^{2}-u_{0}^{2}}\\ f_{v}=\sqrt{l_{5}^{2}+l_{6}^{2}+l_{7}^{2}-v_{0}^{2}}\end{matrix}\right.$