单源最短路径spfa模板（pascal）洛谷P3371

题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入输出格式

输入格式：

第一行包含三个整数N、M、S，分别表示点的个数、有向边的个数、出发点的编号。

接下来M行每行包含三个整数Fi、Gi、Wi，分别表示第i条有向边的出发点、目标点和长度。

输出格式：

一行，包含N个用空格分隔的整数，其中第i个整数表示从点S出发到点i的最短路径长度（若S=i则最短路径长度为0，若从点S无法到达点i，则最短路径长度为2147483647）

输入输出样例

输入样例#1：

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

输出样例#1：

0 2 4 3

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=15

对于40%的数据：N<=100，M<=10000

对于70%的数据：N<=1000，M<=100000

对于100%的数据：N<=10000，M<=500000

样例说明：

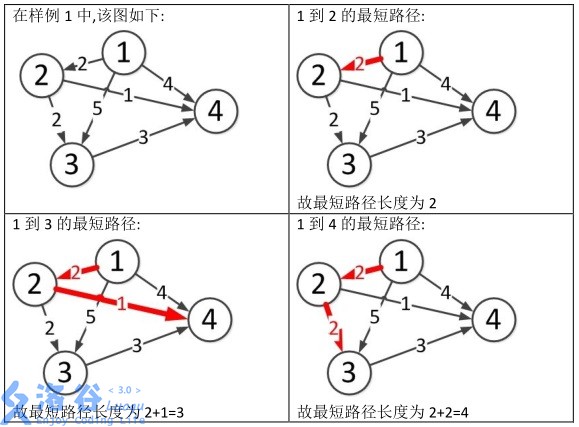
明天要市赛了，复习一些模板。

 program rrr(input,output);
 const
   inf=;
 type
   etype=record
      t,w,next:longint;
   end;
 var
   e:array[..]of etype;
   a,q,dis:array[..]of longint;
   inq:array[..]of boolean;
   n,m,s,i,h,t,u,v,w,cnt:longint;
 procedure add(u,v,w:longint);
 begin
    inc(cnt);e[cnt].t:=v;e[cnt].w:=w;e[cnt].next:=a[u];a[u]:=cnt;
 end;
 begin
    assign(input,'r.in');assign(output,'r.out');reset(input);rewrite(output);
    readln(n,m,s);
    fillchar(a,sizeof(a),);
    for i:= to m do begin read(u,v,w);add(u,v,w); end;
    fillchar(inq,sizeof(inq),false);
    for i:= to n do dis[i]:=inf;
    h:=;t:=;q[]:=s;dis[s]:=;inq[s]:=true;
    while h<>t do
       begin
          inc(h);if h> then h:=;
          i:=a[q[h]];
          while i<> do
             begin
                if dis[q[h]]+e[i].w<dis[e[i].t] then
                   begin
                      dis[e[i].t]:=dis[q[h]]+e[i].w;
                      if not inq[e[i].t] then
                         begin
                            inq[e[i].t]:=true;
                            inc(t);if t> then t:=;q[t]:=e[i].t;
                         end;
                   end;
                i:=e[i].next;
             end;
          inq[q[h]]:=false;
       end;
    for i:= to n do if dis[i]=inf then write(maxlongint,' ') else write(dis[i],' ');
    close(input);close(output);
 end.