【bzoj4195】【NOI2015】程序自动分析

4195: [Noi2015]程序自动分析

Time Limit: 10 Sec  Memory Limit: 512 MB
Submit: 3470  Solved: 1626
[Submit][Status][Discuss]

Description

在实现程序自动分析的过程中,常常需要判定一些约束条件是否能被同时满足。

考虑一个约束满足问题的简化版本：假设x1,x2,x3,…代表程序中出现的变量，给定n个形如xi=xj或xi≠xj的变量相等/不等的约束条件，请判定是否可以分别为每一个变量赋予恰当的值，使得上述所有约束条件同时被满足。例如，一个问题中的约束条件为：x1=x2，x2=x3，x3=x4，x1≠x4，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足。

现在给出一些约束满足问题，请分别对它们进行判定。

Input

输入文件的第1行包含1个正整数t，表示需要判定的问题个数。注意这些问题之间是相互独立的。

对于每个问题，包含若干行：

第1行包含1个正整数n，表示该问题中需要被满足的约束条件个数。

接下来n行，每行包括3个整数i,j,e，描述1个相等/不等的约束条件，相邻整数之间用单个空格隔开。若e=1，则该约束条件为xi=xj；若e=0，则该约束条件为xi≠xj。

1≤n≤1000000

1≤i,j≤1000000000

题解：

这题可以离线，并且是对整体进行询问，直接离线所有判断，然后并查集合并所有等号，对不等号一一判断即可；

想说的是这个题的在线版本(ORZ  wwwwodddd)

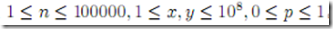
       大致就是在线了然后回答每一个询问；

依旧用并查集，但是用set对每个并查集维护一个敌人集合，然后合并两个集合的时候启发式合并set即可，需要离散化；(两份代码都放了OVO)

复杂度O(nlogn)

 #include<bits/stdc++.h>
 using namespace std;
 const int N=;
 int T,n,tot,tx[N],ty[N],cnt,fa[N];
 map<int,int>mp;
 int get(int x){
     if(!mp[x])mp[x]=++tot,fa[tot]=tot;
     return mp[x];
 }
 int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
 int main(){
 //  freopen("bzoj4195.in","r",stdin);
 //  freopen("bzoj4195.out","w",stdout);
     scanf("%d",&T);
     while(T--){
         scanf("%d",&n);
         tot=cnt=;mp.clear();
         for(int i=,x,y,e;i<=n;i++){
             scanf("%d%d%d",&x,&y,&e);
             x=get(x);y=get(y);
             if(e){
                 int fx=find(x),fy=find(y);
                 if(fx!=fy)fa[fx]=fy;
             }else tx[++cnt]=x,ty[cnt]=y;
         }
         int fg=;
         for(int i=;i<=cnt;i++)if(find(tx[i])==find(ty[i])){fg=;break;}
         puts(fg?"NO":"YES");
     }
     return ;
 }

离线版本

 #include<cstdio>
 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<queue>
 #include<cmath>
 #include<vector>
 #include<stack>
 #include<map>
 #include<set>
 #define Run(i,l,r) for(int i=l;i<=r;i++)
 #define Don(i,l,r) for(int i=l;i>=r;i--)
 #define ll long long
 #define inf 0x3f3f3f3f
 using namespace std;
 const int N=;
 int n,m,sub[N],tot,fa[N];
 struct data{
     int x,y,p;
     data(int _x=,int _y=,int _p=):x(_x),y(_y),p(_p){};
 }A[N];
 set<int>s[N];
 set<int>::iterator it;
 char gc(){
     static char*p1,*p2,S[];
     if(p1==p2)p2=(p1=S)+fread(S,,,stdin);
     return(p1==p2)?EOF:*p1++;
 }
 int rd(){
     int x=,f=; char c=gc();
     while(c<''||c>''){if(c=='-')f=-;c=gc();}
     while(c>=''&&c<='')x=(x<<)+(x<<)+c-'',c=gc();
     return x*f;
 }
 int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
 bool check(int x,int y){
     if(x==y)return false;
     if(s[x].size()>s[y].size())swap(x,y);
     for(it=s[x].begin();it!=s[x].end();it++){
         if(find(*it)==y)return true;
     }
     fa[x]=y;
     for(it=s[x].begin();it!=s[x].end();it++){
         s[y].insert(find(*it));
     }
     s[x].clear();
     return false;
 }
 int main(){
 //  freopen("mzoj1292.in","r",stdin);
 //  freopen("mzoj1292.out","w",stdout);
     //scanf("%d",&n);
     n=rd();
     Run(i,,n){
         //A[i]=(data){rd(),rd(),rd()};
         //scanf("%d%d%d",&A[i].x,&A[i].y,&A[i].p);
         A[i].x=rd(); A[i].y=rd(); A[i].p=rd();
         sub[++tot]=A[i].x , sub[++tot]=A[i].y;
     }
     sort(sub+,sub+tot+);
     tot=unique(sub+,sub+tot+)-sub-;
     Run(i,,tot)fa[i]=i;
     for(int i=,x,y;i<=n;i++){
         x=A[i].x=lower_bound(sub+,sub+tot+,A[i].x)-sub;
         y=A[i].y=lower_bound(sub+,sub+tot+,A[i].y)-sub;
         if(A[i].p==){
             if(find(x)==find(y)){puts("No");continue;}
             puts("Yes");
             s[fa[x]].insert(fa[y]);
             s[fa[y]].insert(fa[x]);
         }else {
             int fx=find(x) , fy=find(y);
             if(check(fx,fy)){puts("No");continue;}
             else puts("Yes");
         }
     }
     return ;
 }//by tkys_Austin;

在线版本