一些动态规划问题的java实现

从上往下推公式，从下往上求解值。

一：矩阵链乘法，最小括号化方案，动态规划方程。

0        如果i=j

m[i,j]  ={

min[i,k]+m[k+1,j]+p_i-1p_kp_{j          如果  i<j}  

子问题涉及到子问题起始点和终止点 i , j 的 ，要用三层for循环。

第一层循环代表子问题的长度。

第二层for循环代表 子问题的 起始点。

第三层for循环在  子问题起始点和终止点之间找一个最优的分割点。 需用到动态规划公式。

1：求最小的矩阵，也就是两个相邻的矩阵 。两个相邻矩阵相乘之后，将会组成一个新的矩阵。行列为两个相乘矩阵的左行右列。

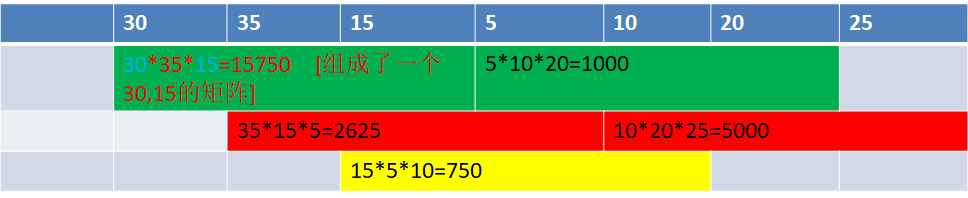
2：求长度为3的矩阵的计算次数，

例如求30,35,15,5组成的3个矩阵的计算次数。

用到1的结果：  30,35,15 得到的矩阵A[30,15]和计算次数15750,  35,15,5得到的矩阵B [35,5] 和计算次数  2625。

[30,35,15,5]=min{(30*15*5+15750) , 30*35*5+2625}.

以此类推...

java代码:

package com.li.chapter15.class02;

/**
 * 矩阵链乘法:使用动态规划方法
 */
public class JuZhenLianChengFa {

    public static void main(String[] args){
        int[] p={30,35,15,5,10,20,25};  //p.length-1个矩阵
        matrixChainOrder(p);
    }

    public static void matrixChainOrder(int[] p) {  //p个矩阵，要用p.length+1个数字来表示。例如两个矩阵相乘要用p0*p1*p2表示，p1是p0的列，p2的行
        int[][] m = new int[p.length-1][p.length-1];   //保存
//        int[][] s = new int[p.length - 1][p.length-1];

        for (int i = 0; i < m.length; i++) {
            m[i][i]=0;  //矩阵链长度为0时，乘积为0,m[j][j+0];
        }

        //p.length=3;
        for (int i = 1; i < p.length - 1; i++) {  // i 矩阵链的长度
            for (int j = 0; j < p.length-i-1; j++) {  //j从0到p.lenght-i-1，子问题的起始点   计算长度为i的矩阵链，所有的最优值。
                m[j][j+i]=Integer.MAX_VALUE;   //最大值。
                for (int k = j; k < j+i; k++) {   //求j到j+i这段长度乘积的最小值，  k是分割点
                    int value = m[j][k] + m[k + 1][j + i] + p[j]*p[k+1] * p[j+i+1];  //k为分割点时，乘积的大小
                    if (value < m[j][j + i]) {
                        m[j][j+i]=value;
//                        s[j][j + i]=k;  //j到j+i这段矩阵链最优分割点为 k
                    }
                }
            }
        }

        for (int i = 0; i < m.length; i++) {
            for (int j = 0; j < m[1].length; j++) {
                System.out.print(m[i][j]+"             ");
            }
            System.out.println("");
        }
        System.out.println(m[1][4]);
    }
}

二：动态规划字符串匹配，  求字符串最大匹配长度。

给定两个字符串，str1="adef";   str2="bdfg";    求字符串最大的匹配个数。

将字符串化为字符数组进行匹配

1：判断最后一个字符串是否匹配，如果不匹配，那么使用就是其中一个字符串减去最后一个字符，再重新匹配。取两者中的较大值。

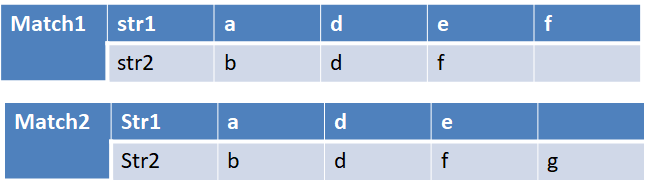
2：

求Match1  这两个字符串匹配的长度。

如果最后一个字符串相同。那么就是将两个字符串都去掉最后一个字符，然后对剩余的字符串进行匹配得到匹配长度，然后加1（刚刚匹配的这一个字符）。

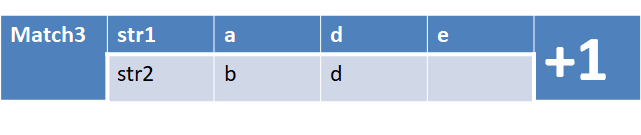
以此类推，得到公式：

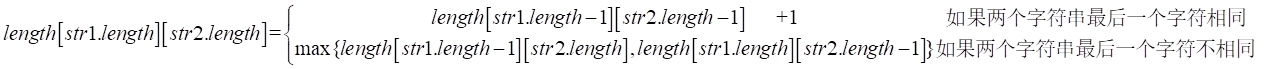
java代码：

package com.li.dynamic;

/**
 * @program: GradleTestUseSubModule
 * @author: Yafei Li
 * @create: 2018-08-02 17:14
 * https://www.cnblogs.com/wuyuegb2312/p/3281264.html
 *   字符串相似度。
 *   动态规划求解
 **/
public class ZiFuChuanXiangShiDu {
    public static void main(String[] args){
        String str1 = "wbdsakfieudfkdfg";
        String str2 = "isdfkjiekdjfkajg";

        char[] chars1 = str1.toCharArray();
        char[] chars2 = str2.toCharArray();

        int[][] arrs = new int[chars1.length][chars2.length];
        for (int i = 0; i < chars1.length; i++) {
            if (chars1[i] == chars2[0]) {
                arrs[i][0]=1;
            }
        }
        for (int i = 0; i < chars2.length; i++) {
            if (chars2[i] == chars1[0]) {
                arrs[0][i]=1;
            }
        }

        for (int i = 1; i < chars1.length; i++) {
            for (int j = 1; j < chars2.length; j++) {
                if (chars1[i] == chars2[j]) {
                    arrs[i][j] = arrs[i - 1][j - 1]+1;
                }else {
                    if (arrs[i - 1][j] > arrs[i][j - 1]) {
                        arrs[i][j]=arrs[i - 1][j];
                    }else {
                        arrs[i][j]=arrs[i][j-1];
                    }
                }
            }
        }

        for (int i = 0; i < arrs.length; i++) {
            for (int j = 0; j < arrs[0].length; j++) {
                System.out.print(arrs[i][j]+"   ");
            }
            System.out.println("");
        }
    }
}

https://www.cnblogs.com/wuyuegb2312/p/3281264.html

动态规划，主要要找到一个问题的最优子结构。

哪个变量作为子结构的变量。

变量：看哪个变量重复。

看哪个变量的集合能够分出一个更小的子集。且完全无关。一般都有多个变量作为子结构的变量。