感知机PLA算法实现[转载]

转自:https://blog.csdn.net/u010626937/article/details/72896144#commentBox

1.实现原始形式

import numpy as np
import matplotlib.pyplot as plt

#1、创建数据集
def createdata():
    samples=np.array([[3,-3],[4,-3],[1,1],[1,2]])#4行2列
    labels=[-1,-1,1,1]
    return samples,labels

#训练感知机模型
class Perceptron:
    def __init__(self,x,y,a=1):
        self.x=x
        self.y=y
        self.w=np.zeros((x.shape[1],1))#初始化权重，w1,w2均为0
        self.b=0
        self.a=1#学习率
        self.numsamples=self.x.shape[0]
        self.numfeatures=self.x.shape[1]

    def sign(self,w,b,x):
        y=np.dot(x,w)+b
        return int(y)

    def update(self,label_i,data_i):
        tmp=label_i*self.a*data_i
        tmp=tmp.reshape(self.w.shape)#转换成w的形状。
        #更新w和b
        self.w=tmp+self.w
        self.b=self.b+label_i*self.a

    def train(self):
        isFind=False
        while not isFind:
            count=0
            for i in range(self.numsamples):
                tmpY=self.sign(self.w,self.b,self.x[i,:])
                if tmpY*self.y[i]<=0:#如果是一个误分类实例点
                    print ('误分类点为：',self.x[i,:],'此时的w和b为：',self.w,self.b)
                    count+=1
                    self.update(self.y[i],self.x[i,:])#更新
            if count==0:
                print ('最终训练得到的w和b为：',self.w,self.b)
                isFind=True
        return self.w,self.b

#画图描绘
class Picture:
    def __init__(self,data,w,b):
        self.b=b
        self.w=w
        plt.figure(1)
        plt.title('Perceptron Learning Algorithm',size=14)
        plt.xlabel('x0-axis',size=14)
        plt.ylabel('x1-axis',size=14)

        xData=np.linspace(0,5,100)#start stop 要生成的样本数，是一个array
        yData=self.expression(xData)#
        plt.plot(xData,yData,color='r',label='sample data')

        plt.scatter(data[0][0],data[0][1],s=50)
        plt.scatter(data[1][0],data[1][1],s=50)
        plt.scatter(data[2][0],data[2][1],s=50,marker='x')
        plt.scatter(data[3][0],data[3][1],s=50,marker='x')
        plt.savefig('2d.png',dpi=75)

    def expression(self,x):#只是为了画出这一条直线。
        y=(-self.b-self.w[0]*x)/self.w[1]#注意在此，把x0，x1当做两个坐标轴，把x1当做自变量，x2为因变量
        return y

    def Show(self):
        plt.show()

if __name__ == '__main__':
    samples,labels=createdata()
    myperceptron=Perceptron(x=samples,y=labels)
    weights,bias=myperceptron.train()
    Picture=Picture(samples,weights,bias)
    Picture.Show()

运行结果：

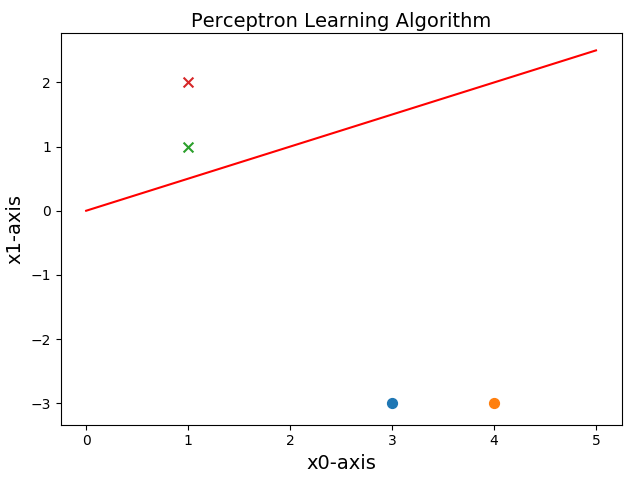
误分类点为： [ 3 -3] 此时的w和b为： [[0.]
 [0.]] 0
误分类点为： [1 1] 此时的w和b为： [[-3.]
 [ 3.]] -1
最终训练得到的w和b为： [[-2.]
 [ 4.]] 0

//真是太厉害了。

2.实现对偶形式

import numpy as np
import matplotlib.pyplot as plt

#1、创建数据集
def createdata():
    samples=np.array([[3,-3],[4,-3],[1,1],[1,2]])
    labels=np.array([-1,-1,1,1])
    return samples,labels

#训练感知机模型
class Perceptron:
    def __init__(self,x,y,a=1):
        self.x=x
        self.y=y
        self.w=np.zeros((1,x.shape[0]))#1行4列
        self.b=0
        self.a=1#学习率
        self.numsamples=self.x.shape[0]
        self.numfeatures=self.x.shape[1]
        self.gMatrix=self.cal_gram(self.x)

    def cal_gram(self,x):
        gMatrix=np.zeros((self.numsamples,self.numsamples))
        for i in range(self.numsamples):
            for j in range(self.numsamples):
                gMatrix[i][j]=np.dot(self.x[i,:],self.x[j,:])
        return gMatrix

    def sign(self,w,b,key):
        y=np.dot(w*self.y,self.gMatrix[:,key])+b
        return int(y)

    def update(self,i):
        print(i,'@@@iii')
        self.w[:,i]=self.w[:,i]+self.a
        self.b=self.b+self.y[i]*self.a

    def cal_w(self):
        w=np.dot(self.w*self.y,self.x)
        return w

    def train(self):
        isFind=False
        while not isFind:
            count=0
            for i in range(self.numsamples):
                tmpY=self.sign(self.w,self.b,i)
                if tmpY*self.y[i]<=0:#如果是一个误分类实例点
                    print('误分类点为：',self.x[i,:],'此时的w和b为：',self.cal_w(),',',self.b)
                    count+=1
                    self.update(i)
            if count==0:
                print ('最终训练得到的w和b为：',self.cal_w(),',',self.b)
                print(self.w)
                isFind=True
        weights=self.cal_w()
        return weights,self.b

#画图描绘
class Picture:
    def __init__(self,data,w,b):
        self.b=b
        self.w=w
        plt.figure(1)
        plt.title('Perceptron Learning Algorithm',size=14)
        plt.xlabel('x0-axis',size=14)
        plt.ylabel('x1-axis',size=14)

        xData=np.linspace(0,5,100)
        yData=self.expression(xData)
        plt.plot(xData,yData,color='r',label='sample data')

        plt.scatter(data[0][0],data[0][1],s=50)
        plt.scatter(data[1][0],data[1][1],s=50)
        plt.scatter(data[2][0],data[2][1],s=50,marker='x')
        plt.scatter(data[3][0],data[3][1],s=50,marker='x')
        plt.savefig('2d.png',dpi=75)

    def expression(self,x):
        y=(-self.b-self.w[:,0]*x)/self.w[:,1]
        return y

    def Show(self):
        plt.show()

if __name__ == '__main__':

    samples,labels=createdata()
    myperceptron=Perceptron(x=samples,y=labels)
    weights,bias=myperceptron.train()
    Picture=Picture(samples,weights,bias)
    Picture.Show()

//注：原博主的update的函数有误，应该是对w的列+a，而不是行。。。现在已经更改。 结果也是正确的结果。

运行结果：

误分类点为： [ 3 -3] 此时的w和b为： [[0. 0.]] , 0
0 @@@iii
误分类点为： [1 1] 此时的w和b为： [[-3. 3.]] , -1
2 @@@iii
最终训练得到的w和b为： [[-2. 4.]] , 0
[[1. 0. 1. 0.]]

注：最后一行是——w。

讨论：

转：https://blog.csdn.net/qq_28618765/article/details/78083179

dot()函数是矩阵乘，而*则表示逐个元素相乘

以及关于这个向量和矩阵乘法的问题：

array对于这种shape函数结果是(3,)类型的，它在运算时是十分灵活的，既可以作为列向量，也可以作为行向量。

import numpy as np

x=[[1,2,3],[4,5,6]]
y=[1,2,3]
xy=np.dot(x,y)
print(xy,xy.shape)

z=[1,2]
xy2=np.dot(z,x)
print(xy2,xy2.shape)

结果：

[14 32] (2,)
[ 9 12 15] (3,)

对于y右乘x，是作为列向量处理了；对于z坐成x，是作为行向量处理了。

3.关于矩阵运算的一些坑试跳

import numpy as np

x=[[1,1,1,1]]
#print(x.shape)
#报错：AttributeError: 'list' object has no attribute 'shape'

y=[1,1,1,1]
#print(y.shape)
#报错：AttributeError: 'list' object has no attribute 'shape'

z=np.array([1,1,1,1])
print(z.shape)
#输出:(4,)

z[2,]=z[2,]+1
print(z)
#输出：[1 1 2 1]

u=np.matrix([1,2,3,4])
print(u.shape)
#输出：(1, 4)

u[:,1]=u[:,1]+1
print(u)
#输出:[[1 3 3 4]]

#u[1,]=u[1,]+10
#print(u)
#输出：IndexError: index 1 is out of bounds for axis 0 with size 1

print(u[0,])
#输出：[[1 3 3 4]]

u[:,1]=u[:,1]+10
print(u)
#输出：[[ 1 13  3  4]]

print(u[0])
#输出：[[ 1 13  3  4]]
#说明：取矩阵的一行是可以使用u[1]或者u[1,]的
#但是取矩阵的一列必须使用:，u[:,1]，否则会报错。