0921 LCA练习

1.poj 1330

数据结构中的树，在计算机科学中是非常重要的，例如我们来看看下面这棵树：

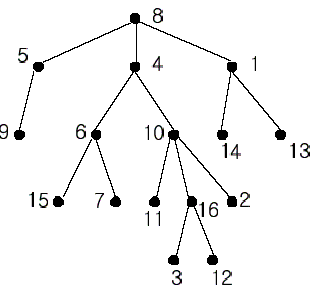
在图中我们对每个节点都有编号了。 8号节点是这棵树的根。我们定义，一个子节点向它的根节点的路径上，任意一个节点都称为它的祖先。例如， 4号节点是16号节点的祖先。而10号节点同样也是16号的祖先。事实上，16号的祖先有8，4，10，16共四个。另外8， 4， 6，7都是7号节点的祖先，所以7号和16号的公共祖先是4和8号，而在这两个里面，4号是距离7和16最近的一个，所以我们称7号和16号的最近公共祖先是4号。

再例如，2和3的最近公共祖先是10，再例如6和13的是8。

现在你需要编写一个程序，在一棵树中找出指定两个节点的最近公共祖先

Input

第一行输入T表示有T组数据。每组第一行是N表示这棵树有多少个节点，其中 2<=N<=10,000。 节点用正整数1, 2,..., N表示。 接下来的 N -1 行表示这棵树的边，每行两个数，都是节点编号，前一个是后一个的父节点。最后一行是要查询的两个节点，计算出这两个节点的最近公共祖先

Output

对于每组测试输出一行，输出它们的最近公共祖先的编号。

分析:lca

代码:

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
using namespace std;
#define maxn 10005
int n,m,s;
int cnt,head[maxn],depth[maxn],p[maxn][25],fat[500005];
struct node{
	int nxt,to;
}e[maxn];
void add(int x,int y){
	e[++cnt].nxt=head[x];
	head[x]=cnt;
	e[cnt].to=y;
    fat[y]=x;
}
void pre(int u,int fa){
    depth[u]=depth[fa]+1;
    p[u][0]=fa;
    for(int i=1;1<<i<=depth[u];i++)p[u][i]=p[p[u][i-1]][i-1];
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v!=fa)pre(v,u);
    }
}
int lca(int a,int b){
    if(depth[a]>depth[b])swap(a,b);
    for(int i=20;i>=0;i--){
        if(depth[a]<=depth[b]-(1<<i))b=p[b][i];
    }
    if(a==b)return a;
    for(int i=20;i>=0;i--){
        if(p[a][i]==p[b][i])continue;
        else a=p[a][i],b=p[b][i];
    }
    return p[a][0];
}
int main(){
    int t;scanf("%d",&t);
    while(t--){
        memset(head,0,sizeof(head));
        memset(depth,0,sizeof(depth));
        memset(p,0,sizeof(p));
        memset(fat,0,sizeof(fat));
        memset(e,0,sizeof(e));
        cnt=0;
        scanf("%d",&n);
        for(int i=1;i<n;i++){
            int x,y;scanf("%d%d",&x,&y);
            add(x,y);
        }
        for(int i=1;i<=n;i++){
            if(!fat[i]){
                s=i;
                break;
            }
        }
        pre(s,0);
        int a,b;scanf("%d%d",&a,&b);
        printf("%d\n",lca(a,b));
    }
    return 0;
}

T3 P4281

题目描述

欢乐岛上有个非常好玩的游戏，叫做“紧急集合”。在岛上分散有 nnn 个等待点，有 n−1n-1n−1 条道路连接着它们，每一条道路都连接某两个等待点，且通过这些道路可以走遍所有的等待点，通过道路从一个点到另一个点要花费一个游戏币。

参加游戏的人三人一组，开始的时候，所有人员均任意分散在各个等待点上（每个点同时允许多个人等待），每个人均带有足够多的游戏币（用于支付使用道路的花费）、地图（标明等待点之间道路连接的情况）以及对话机（用于和同组的成员联系）。当集合号吹响后，每组成员之间迅速联系，了解到自己组所有成员所在的等待点后，迅速在 nnn 个等待点中确定一个集结点，组内所有成员将在该集合点集合，集合所用花费最少的组将是游戏的赢家。

小可可和他的朋友邀请你一起参加这个游戏，由你来选择集合点，聪明的你能够完成这个任务，帮助小可可赢得游戏吗？

输入格式

第一行两个正整数 nnn 和 mmm，分别表示等待点的个数（等待点也从 111 到 nnn 进行编号）和获奖所需要完成集合的次数。随后 n−1n-1n−1 行，每行两个正整数 a,ba,ba,b，表示编号为 aaa 和编号为 bbb 的等待点之间有一条路。随后 mmm 行，每行用三个正整数 x,y,zx,y,zx,y,z，表示某次集合前小可可、小可可的朋友以及你所在等待点的编号。

输出格式

输出共 mmm 行，每行两个用空格隔开的整数 p,cp,cp,c。其中第 iii 行表示第 iii 次集合点选择在编号为 ppp 的等待点，集合总共的花费是 ccc 个游戏币。

分析:

经分析,对每两个点求lca,三个点一定有其中两个lca相同,并在另一个lca上面,下面的lca一定是到三点路径并最小的，正确性显然。

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
#define maxn 500005
int n,m,s;
int cnt,head[maxn],depth[maxn],p[maxn][25],fat[maxn];
struct node{
	int nxt,to;
}e[2*maxn];
void add(int x,int y){
	e[++cnt].nxt=head[x];
	head[x]=cnt;
	e[cnt].to=y;
}
void pre(int u,int fa){
    depth[u]=depth[fa]+1;
    fat[u]=fa;
    p[u][0]=fa;
    for(int i=1;1<<i<=depth[u];i++)p[u][i]=p[p[u][i-1]][i-1];
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v!=fa)pre(v,u);
    }
}
int lca(int a,int b){
    if(depth[a]>depth[b])swap(a,b);
    for(int i=20;i>=0;i--){
        if(depth[a]<=depth[p[b][i]])b=p[b][i];//printf("$$$$%d %d\n",i,b);
    }
    //printf("%d %d\n",a,b);
    if(a==b)return a;
    for(int i=20;i>=0;i--){
        if(p[a][i]==p[b][i])continue;
        else a=p[a][i],b=p[b][i];
    }
    return p[a][0];
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<n;i++){
        int a,b;scanf("%d%d",&a,&b);
        add(a,b);add(b,a);
    }
    pre(1,0);
    //printf("sidjhsdl%d\n",depth[0]);
    //for(int i=1;i<=n;i++){
    // printf("%d",depth[i]);
    // }
    for(int i=1;i<=m;i++){
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        int aa=lca(x,y);
        int bb=lca(x,z);
        int cc=lca(y,z);
        // printf("%d %d %d\n",aa,bb,cc);
        int t;
        if(aa==bb)t=cc;
        if(aa==cc)t=bb;
        if(bb==cc)t=aa;
        printf("%d %d\n",t,depth[x]+depth[y]+depth[z]-depth[aa]-depth[bb]-depth[cc]);
    }
    return 0;
}