LeetCode周赛#207

5519. 重新排列单词间的空格 #字符串 #模拟

题目链接

题意

给定字符串text，该字符串由若干被空格包围的单词组成，也就说两个单词之间至少存在一个空格。现要你重新排列空格，使每对相邻单词间空格数目都相等，并尽可能最大化该数目。若不能重新平均分配所有空格，请将多余的空格放置在字符串末尾，这也意味着返回的字符串应当与原text字符串的长度相等。

class Solution {
public:
    string reorderSpaces(string text) {
        int spacenum = 0, words = 0;
        vector<int> pos;
        for (int i = 0; i < text.size(); i++){
            if(text[i] != ' '){
                pos.push_back(i);
                while(i < text.size() && text[i] != ' ') i++;
                words++;
            }
            if(text[i] == ' ') spacenum++;
        }
        if(spacenum == 0) return text;
        int last = (words <= 1) ? spacenum : (spacenum % (words - 1));
        int gap =  (words <= 1) ? 0 : (spacenum / (words - 1));
        string ans;
        for (int i = 0; i < pos.size(); i ++){
            int j = pos[i];
            while(j < text.size() && text[j] != ' ') ans += text[j++];
            if(i != pos.size() - 1) ans += string(gap, ' ');
        }
        ans += string(last, ' ');
        return ans;
    }
};

5520. 拆分字符串使唯一子字符串的数目最大 #深搜 #哈希表

题目链接

题意

给定字符串s，请拆分该字符串，使得拆分出来的若干非空子字符串连接后能够还原为原字符串，返回拆分后唯一子字符串的最大数目。

分析

起初我采用的是贪心策略qaq，将当前未访问过的子串加入map，如果访问过就将该子串连接上后面的字符。然而"addbsd"串得到的答案应是5，也就说拆分成"a","dd","b","s","d"，贪心的话会拆分成"a","d","db","s"。

观察数据范围，串s的长度最多才16，暴搜可行，递归起点来进行拆分，用map判断该子串是否已出现过。

class Solution {
private:
    unordered_map<string, int> vis;
    int ans = -1;
public:
    void DFS(string s, int start, int cnt){
        if(start == s.size())
            ans = max(ans, cnt);
        else if(cnt + (int)s.size() - start + 1 < ans) //注意s.size()一定要强制转换下
            return; //剪枝，此情况说明，无论如何划分都无法超过ans值
        else {
            string tmp;
            for (int i = start; i < s.size(); i++){
                tmp += s[i];
                if(vis[tmp] == 0){
                    vis[tmp]++;
                    DFS(s, i + 1, cnt + 1);
                    vis[tmp]--;
                }
            }
        }
    }
    int maxUniqueSplit(string s) {
        DFS(s, 0, 0);
        return ans;
    }
};

5521. 矩阵的最大非负积 #深搜 #动态规划

题目链接

题意

给定rows*cols的矩阵，矩阵每个元素有一整数(可正可负)，你从(0,0)出发，只能向右或向下移动。从(0,0)到达(rows-1, cols-1)的所有路径中，找出具有最大非负积的路径，路径之积为沿路径访问的单元格中所有整数的乘积。对最后返回的最大非负积取余，若该结果为负值，则返回-1

分析

• DFS版本(\(1856ms\)奇慢)

typedef long long ll;
class Solution {
private:
    ll ans = -1;
    const int MOD = 1e9 + 7;
public:
    void DFS(vector<vector<int>>& grid, int x, int y, ll sum){
        if((x == grid.size() - 1 && y == grid[x].size() - 1) || sum == 0) {
            ans = max(ans, sum); //注意sum==0剪枝，否则超时
            return;
        }
        if(x != grid.size() - 1)
            DFS(grid, x + 1, y, (sum * (ll)grid[x + 1][y]));
        if(y != grid[x].size() - 1)
            DFS(grid, x, y + 1, (sum * (ll)grid[x][y + 1]));
    }
    int maxProductPath(vector<vector<int>>& grid) {
        DFS(grid, 0, 0, (ll)grid[0][0]);
        return ans % MOD; //由于涉及到值间比较，只对最后结果取模即可
    }
};

• DP版本(\(8ms\))

我们定义一个三维数组DP[i][j][0\1]，代表从(0,0)到达(i,j)的最小乘积和最大乘积。为什么要维护两个最值，考虑到乘积的过程中会遇到负数，最大之积乘上负数便成为最小之积了。此外，未到达终点之前移动过程中得到的负数，在后面有机会被另一负数抵消为正数，因而需要维护这两个最值。注意，遇到负数时，即变号的过程，要切换两个最值。

typedef long long ll;
class Solution {
private:
    const int MOD = 1e9 + 7;
    ll DP[16][16][2];
public:
    int maxProductPath(vector<vector<int>>& grid) {
        DP[0][0][1] = DP[0][0][0] = grid[0][0];
        int n = grid.size(), m = grid[0].size();
        for(int i = 1; i < n; i++) //初始化边界，只有一个方向无需选择
            DP[i][0][0] = DP[i][0][1] = DP[i - 1][0][1] * (ll)grid[i][0];
        for(int j = 1; j < m; j++) //初始化边界，只有一个方向无需选择
            DP[0][j][0] = DP[0][j][1] = DP[0][j - 1][1] * (ll)grid[0][j];
        for(int i = 1; i < n; i++){
            for(int j = 1; j < m; j++){
                if(grid[i][j] == 0) continue;
                else if(grid[i][j] > 0){ //不用变号
                    DP[i][j][1] = max(DP[i][j - 1][1] * (ll)grid[i][j], DP[i - 1][j][1] * (ll)grid[i][j]);
                    DP[i][j][0] = min(DP[i][j - 1][0] * (ll)grid[i][j], DP[i - 1][j][0] * (ll)grid[i][j]);
                }
                else if(grid[i][j] < 0){ //乘上grid[i][j]会使结果变号
                    DP[i][j][1] = max(DP[i][j - 1][0] * (ll)grid[i][j], DP[i - 1][j][0] * (ll)grid[i][j]); //最大值成负值变为最小值
                    DP[i][j][0] = min(DP[i][j - 1][1] * (ll)grid[i][j], DP[i - 1][j][1] * (ll)grid[i][j]);
                }
            }
        }
        if(DP[n - 1][m - 1][1] < 0) return -1;
        else return DP[n - 1][m - 1][1] % MOD;
    }
};

1595. 连通两组点的最小成本 #状压DP #枚举子集 #滚动数组

题目链接

题意

给定两组点，第一组有size1个点，第二组有size2个点，size1>=size2。给定cost[][]数组，cost[i][j]代表第一组点i和第二组点j的连接成本。现要你将第一组的每个点都必须至少与第二组中一个点连接，且第二组的每个点都必须至少与第一组中的一个点连接，返回连通两组点所需的最小成本。

分析

这道题，让我意识到我状压DP练习得还不够qaq。

由于第一组点的数量大于第二组点，也就说状态比第二组点多，那么定义dp[i][state]代表当前遍历到左侧的第i个节点时，与第二组顶点的连接状态state(二进制意义，连接为1，未连接为0)下，所需的最小成本。

对于左侧第i个节点，它有两种连接方案：

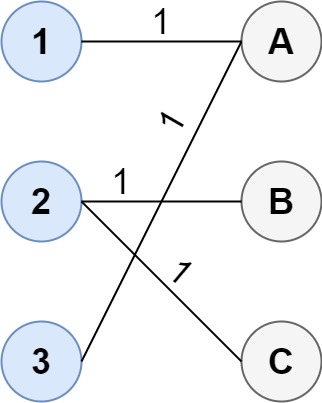
1. 选择右侧中已被连接的一个点，进行连接（保证所有的左侧点均与右侧点相连）。也许你会觉得多余，但是你看上图中的顶点3，它只能与A匹配（之前被顶点1连接过）。

2. 选择右侧中未被连接的若干个点，进行连接。（保证所有右侧点均被左侧点相连）如上图中的顶点2。此处要连接的数量，一时无法确定下来，故需要枚举，也就说枚举当前未连接点状态的子集，我们不妨将这状态反转（未连接的表示1，与上面不同，这样是便于与上一状态进行合并，按位或操作取并集），比如当前状态00111说明，右侧3,4,5点未被左侧点连接，那么该状态子集为00001,00010,00011,….。

   [位运算枚举子集的方法]：参考自@lucifer1004的笔记

   模板即为

   for(int state = 0; state < mymax; state++){ //枚举所有状态
       int rest = ....
       for(int subState = res; subState; subState = (subState - 1) & res){
           //....
       } //从后往前，枚举子集：即不断-1的过程中，对状态-1得到的结果与最初母集进行按位和操作，比如"1100"，1100-1=1011，我们看到后面两位的11并不是"1100"的子集，那么将1011按位与1100得到1000，属于1100的子集
   }
   

   对n个元素所有子集进行枚举，时间复杂度\(O(3^n)\)。

状态压缩DP往往能通过滚动数组节省空间，注意到每次迭代左侧的一个顶点时，当前新状态只依赖于上一状态结果即可（即当前顶点的上一个顶点或上一轮循环计算的结果），因而我们可以对dp[i][state]的第一维滚掉，只需定义dp[state]即可。

class Solution {
private:
    int dp[5000];
public:
    int connectTwoGroups(vector<vector<int>>& cost) {
        int n = cost.size(), m = cost[0].size(), mymax = 1 << m;
        for (int i = 0; i <= mymax; i++) dp[i] = 0x3f3f3f3f;
        dp[0] = 0;
        for (int i = 0; i < n; i++) { //迭代每一行（即左侧的每一个顶点）
            int tmp[5000]; for (int i = 0; i <= mymax; i++) tmp[i] = 0x3f3f3f3f;
            for (int state = 0; state < mymax; state++) { //枚举 第二组连接的所有状态
                if (dp[state] == 0x3f3f3f3f) continue; //状态不可达
                /*方案一：对于左侧点，选择右侧已被连接的一个点匹配*/
                for (int j = 0; j < m; j++) {
                    int nextState = state | (1 << j);
                    tmp[nextState] = min(tmp[nextState], dp[state] + cost[i][j]);
                }
                /*方案二：对于右侧点，选择state状态所有未被连接的点的一个子集里的点进行连接。*/
                int rest = (mymax - 1) ^ state; //表示截至第 i 行还没被选过的边（即未连上第二组相应顶点）
                for (int subState = rest; subState; subState = (subState - 1) & rest) { //枚举之前未连接的边的子集
                    int sum = 0;
                    for (int j = 0; j < m; j++) //计算该子集中未连接的边所需要的花费
                        if (subState & (1 << j)) sum += cost[i][j]; //若子集中存在该边，计入
                    int nextState = state | subState; //之前的边 并上 部分之前未连接的边
                    tmp[nextState] = min(tmp[nextState], dp[state] + sum); //更新新状态
                }
            }
            for (int i = 0; i <= mymax; i++) dp[i] = tmp[i]; //滚掉上一轮的状态，更新当前轮的状态，节省空间
        }
        return dp[mymax - 1]; //返回第二组所有顶点均被连上之状态 的 值
    }
};