有向图强连通分量的Tarjan算法及模板

【有向图强连通分量】

在有向图G中，如果两个顶点间至少存在一条路径，称两个顶点强联通（strongly connected），如果有向图G的每两个顶点都强联通，称有向图G是一个强联通图。非强联通图有向图的极大强联通子图（对于“极大”的理解，就是在一个局部子图中不能再大。就像是数学中的求一个函数中的极大值和极小值一样，例如求函数f(x)的极大值和极小值，变量x可以有不同的区间，所以在x的不同区间内就会有不同的极大值或极小值。） 称为强联通分量。直接根据定义用双向遍历取交集求强联通分量，时间复杂度为O（N……2+M）。更好的方法是kosaraju和tarjan算法，两者的时间复杂度都是O（N+M）。先介绍tarjan算法。

（点对（u,v）称为边或弧，若边的点对（u,v）有序则称为有向边，其中u称为tou，v称为尾）

---

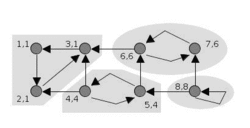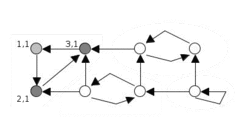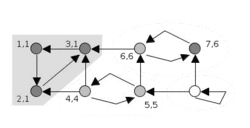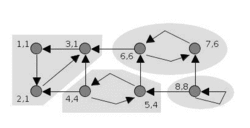
（摘自wiki：https://en.wikipedia.org/wiki/Tarjan%27s_strongly_connected_components_algorithm）

【定义】：

tarjan算法是基于对图深度优先搜索的算法，每个强联通分量为搜索树的一颗子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中节点是否为一个强联通分量。

定义dfn(u)为节点u搜索的次序编号（时间戳），low（u）为u或者u的子树能够追溯到的最早的栈中节点的次序号。//Low[u]是点集{u点及以u点为根的子树}中(所有反向弧)能指向的(离根最近的祖先v)的 DFN[v]值(即v点时间戳) //Low[u]表示以u点为父节点的子树能连接到 [栈中] 最上端的点 的DFN值(换句话说是最小的DFN，因为最上端的DFN是最小的嘛）

由定义可以得：

low(u)=min( dfn(u), low(v), dfn(v));

当dfn(u)=low(u)时，以u为根的搜索子树上的所有节点是一个强连通分量。

【应用】：

Tarjan是一个对图的分析的强有力的算法，主要应用有：有向图的强连通分量、无向图的割点桥与双连通分量、LCA(最近公共祖先)

---

【黑匣子】

先最初调用

1、init()

2、把图用add 存下来，注意图点标为1-n，若是[0,n-1]则给所有点++;

3、调用tarjan_init(n); 再调用suodian();

4、新图就是vector<int>G[];  新图点标从1-tar ;

5、对于原图中的每个点u，都属于新图中的一个新点Belong[u];

新图一定是森林。

6、新图中的点u 所表示的环对应原图中的vector<int> bcc[u];

7、旧图中u在新图中所属的点是Belong[u];

---

Tarjan的实现主体就是dfs。可以自己画一个图感受一下，有向图中，每个强联通分量都是由多个环组成的，且这些环包含了集合中的所有元素且这些环两两相交，那么如果我们对于其中的任意一个元素进行dfs的话，最终这个强连通分量里的元素就会形成一颗子树，并且如果我们把我们的起始元素看作一棵树的根节点的话，那么它的子树中（也就是这个强联通分量中）一定会有节点它的父节点方向连边，并且这些向回连的边最终都会通到根节点，并且叶节点必然会向回连边（这是很显然的）。这样才能满足这个子树中的每个节点都能到达其他的各个节点。

知道了这些性质后，我们就可以进行操作了： 
我们将每个强联通分量视为一个集合，一开始所有节点都是各自独立的集合，开两个数组dfn[ ]和low[ ]，dfn记录的是节点被访问的顺序，low[i]记录i节点所在集合的代表元素的dfn值（这里类似于并查集），显然对于一个新的节点，集合的代表元素就是它本身，dfn[i]=low[i]，。然后我们对其进行dfs，首先将它加入一个栈内，然后对它的每一个可以到达的节点进行dfs，如果它连接的节点是它的一个父节点（或祖父节点，也就是刚刚dfs路径上的点），那么low[i] = min( low[i], low[to] )；如果它连接的节点已经被访问过（也就是已经dfs过）并且不是该节点的父节点或祖父节点，直接跳过（因为既然那个节点已经dfs过，而当前节点又是本次才访问到，那么说明那个节点出发一定不能到达当前节点，也就是说它们一定不在一个强联通分量里）；我们看看上面这部分操作，它和并查集的操作是很像的，我们相当于将dfs路径上的环合并成了一个集合（相交环也被合成了一个集合），并且代表元素是最先访问的那个点，而由定义可知所有相交环都是一个强联通图，那么我们在回溯时，判断该节点的low[ ]是否等于dfn[ ]，如果不相等，那么不做处理，直接返回，如果相等的话就说明该节点是一个集合的代表元素，我们在将刚才栈中的所有在该节点后面入栈的还在栈内的元素（包括它本身）出栈，这些元素就是一个强联通分量。这样的正确性是显然的，我们相当于将所有已经构建的集合保存了下来，而这些集合都是由相交环构成的，而相交环构成的集合一定是一个强联通分量，，所以我们构造出来的集合就一定是原图的强联通分量！

---

【算法伪代码如下】

tarjan(u)
{
    dfn[u]=low[u]=++index  //将节点u设定次序编号和low初值
    stack.push(u)         //将节点u压入栈中
    for each(u,v) in E    //枚举每一条边
        if(v is not visted)  //如果节点v未被访问过
           tarjan(v)           //继续向下找
          low[u]=min(low[u],low[v])
        else if(v in S)        //如果节点还在栈内
          low[u]=min(low[u],dfn[v])
    if(dfn[u]==low[u])    //如果节点u是强联通分量的根
        repeat
            v=s.pop   //将v退栈，为该强连通分量中的一个顶点
            print v
        until (u==v)
}

算法：

void tarjan(int i)
{
    int j;
    dfn[i]=low[i]=++index  //将节点u设定次序编号和low初值
    instack[i]=true;         //将节点u压入栈中
    stap[++stop]=i;
    for(edge *e=v[i]; e; e=e->next)    //枚举每一条边
    {
        j=e->t;
        if(!dfn[j])
        {
            tarjan(j);
            if(low[j]<low[i])
                low[i]=low[j];
        }

        else if(instack[j] && dfn[j]<low[i])
            low[i]=dfn[j];
    }

    if(dfn[i]==low[i])
    {
        cnt++;
        do
        {
            j=stap[stop--];
            instack[j]=false;
            belong[j]=cnt;
        }while(j!=i);
    }
}

void solve()
{
    int i;
    stop=cnt=index=;
    memset(dfn,,sizeof(dfn));
    for(i=; i<=n; i++)
    {
        if(!dfn[i])
            tarjan(i);
    }
}