Tensorflow 笔记：第一讲

一、
基本概念

1、
什么是人工智能

人工智能的概念：
机器模拟人的意识和思维

重要人物：
艾伦·麦席森·图灵（ Alan Mathison Turing）

人物简介： 1912 年 6 月 23 日－1954 年 6 月 7 日，英国数学家、逻辑学家，被称

为计算机科学之父，人工智能之父。

相关事件：（ 1） 1950 年在论文《机器能思考吗？》中提出了图灵测试，一种用于

判定机器是否具有智能的试验方法：提问者和回答者隔开，提问者通过一些装置

（如键盘）向机器随意提问。多次测试，如果有超过 30%的提问者认为回答问题

的是人而不是机器，那么这台机器就通过测试，具有了人工智能。 也就是工智能

的概念："用机器模拟人的意识和思维"。

（ 2）图灵在论文中预测：在 2000 年，会出现通过图灵测试具备人工智能的机器。

然而直到 2014 年 6 月，英国雷丁大学的聊天程序才成功冒充了 13 岁男孩，通过

了图灵测试。这一事件比图灵的预测晚了 14 年。

（ 3） 在 2015 年 11 月 science 杂志封面新闻报道，机器人已经可以依据从未见

过的文字中的一个字符，写出同样风格的字符，说明机器已经具备了迅速学习陌

生文字的创造能力。

2、
什么是机器学习

机器学习的概念：
机器学习是一种统计学方法，计算机利用已有数据得出某种模

型，再利用此模型预测结果。

特点：
随经验的增加，效果会变好。

简单模型举例：
决策树模型

机器学习和传统计算机运算的区别：
传统计算机是基于冯诺依曼结构，指令预先

存储。运行时， CPU 从存储器里逐行读取指令，按部就班逐行执行预先安排好的

指令。
其特点是， 输出结果确定，因为先干什么，后干什么都已经提前写在指令

里了。

机器学习三要素：
数据、算法、算力

3、
什么是深度学习

深度学习的概念：
深层次神经网络，源于对生物脑神经元结构的研究。

人脑神经网络：
随着人的成长，脑神经网络是在渐渐变粗变壮。

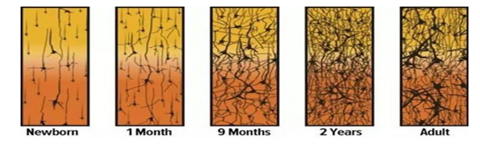
生物学中的神经元：
下图左侧有许多支流汇总在一起，生物学中称这些支流叫做

树突。树突具有接受刺激并将冲动传入细胞体的功能，
是神经元的输入。 这些树

突汇总于细胞核又沿着一条轴突输出。轴突的主要功能是将神经冲动由胞体传至

其他神经元，是神经元的输出。
人脑便是由 860 亿个这样的神经元组成，所有的

思维意识，都以它为基本单元，连接成网络实现的。

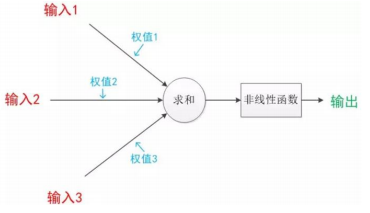
计算机中的神经元模型： 1943 年，心理学家 McCulloch 和数学家 Pitts 参考了

生物神经元的结构，发表了抽象的神经元模型 MP。 神经元模型是一个包含输入，

输出与计算功能的模型。输入可以类比为神经元的树突，输出可以类比为神经元

的轴突，计算可以类比为细胞核。

4、
人工智能 Vs 机器学习 Vs 深度学习

人工智能，就是用机器模拟人的意识和思维。

机器学习，则是实现人工智能的一种方法，是人工智能的子集。

深度学习就是深层次神经网络，是机器学习的一种实现方法，是机器学习的子集。

二、
神经网络的发展历史（三起两落）

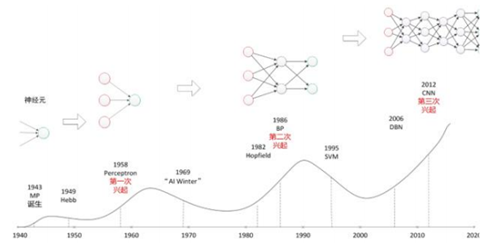
第一次兴起： 1958 年，人们把两层神经元首尾相接，组成单层神经网络，称做感

知机。感知机成了首个可以学习的人工神经网络。引发了神经网络研究的
第一

次兴起。

第一次寒冬： 1969 年，这个领域的权威学者 Minsky 用数学公式证明了只有单

层神经网络的感知机无法对异或逻辑进行分类， Minsky 还指出要想解决异或可

分问题，需要把单层神经网络扩展到两层或者以上。然而在那个年代计算机的运

算能力，是无法支撑这种运算量的。只有一层计算单元的感知机，暴露出他的天

然缺陷，使得神经网络研究进入了第一个寒冬。

第二次兴起： 1986 年， Hinton 等人提出了反向传播方法，有效解决了两层神经

网络的算力问题。引发了神经网络研究的第二次兴起。

第二次寒冬： 1995 年，支持向量机诞生。支持向量机可以免去神经网络需要调节

参数的不足，还避免了神经网络中局部最优的问题。一举击败神经网络，成为当

时人工智能领域的主流算法，使得神经网络进入了他的第二个冬季。

第三次兴起： 2006 年， 深层次神经网络出现， 2012 年， 卷积神经网络在图像识

别领域中的惊人表现，又引发了神经网络研究的再一次兴起。

三、
机器学习的典型应用

1、
应用领域

计算机视觉、语音识别、
自然语言处理

2、
主流应用：

（ 1） 预测（对连续数据进行预测）

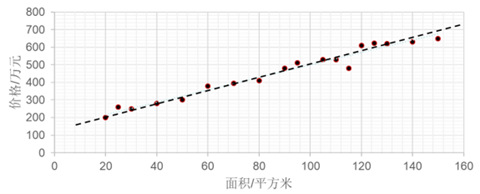
（ 2） 分类（对离散数据进行分类）

四、课程小结

1、
机器学习，就是在任务 T 上，随经验 E 的增加，效果 P 随之增加。

2、
机器学习的过程是通过大量数据的输入，生成一个模型，再利用这个生成的

模型，实现对结果的预测。

3、
庞大的神经网络是基于神经元结构的，是输入乘以权重，再求和，再过非线

性函数的过程。