[COGS 2421] [HZOI 2016] 简单的Treap 笛卡尔树

笛卡尔树就是你给两维限制，一维堆R，一维二叉搜索树K，平地拔起一棵Treap，最广范的应用：用LCA求区间最值，建Treap，还有个什么范围top k我表示并不会查都查不到。它最妙最高的地方在于用栈来建树：我们可以先排序K然后一个个插入，那么我们都是最右端，横容易被卡，那么我们不从上到下，我们从下到上，用栈维护，那就把时间复杂度从O(n^2)降到O(n)，具体过程见下图从图一到图二就是这么一个过程，我们在把K为13的点插入时要找到一个合适的位置，上比他大，下比他小（假设大根堆）

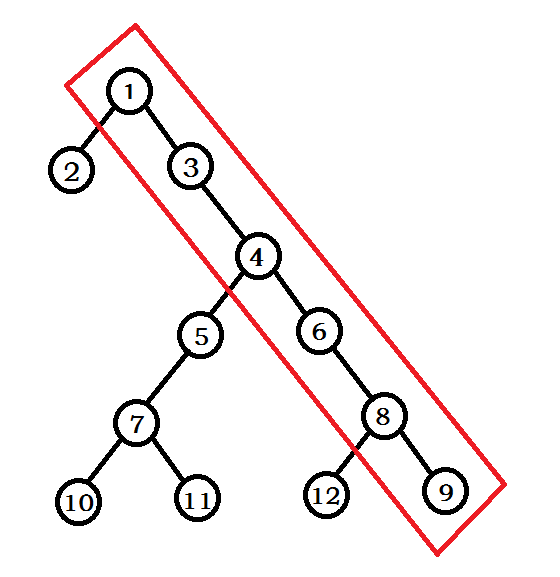
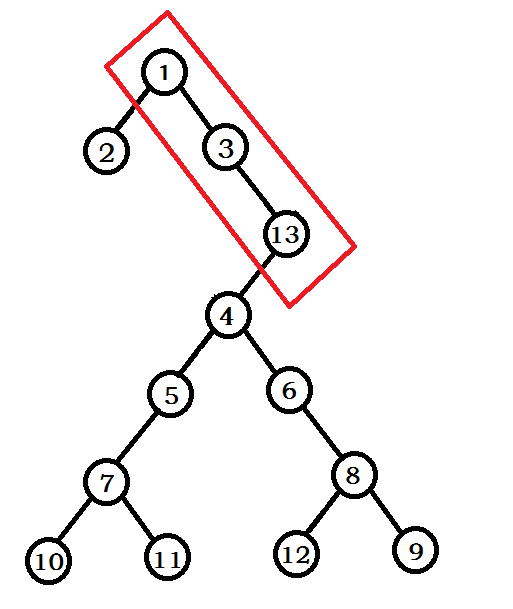
下面见代码

#include<cstdio>
#include<algorithm>
#define MAXN 500010
using namespace std;
inline int read()
{
  int sum=;
  char ch=getchar();
  while(ch<''||ch>'')ch=getchar();
  while(ch>=''&&ch<='')
  {
    sum=(sum<<)+(sum<<)+ch-'';
    ch=getchar();
  }
  return sum;
}
struct Treap
{
  int key,r;
  Treap *ch[];
}*stack[MAXN],node[MAXN],*root;
int top;
int n;
int comp(const Treap a,const Treap b)
{
  return a.key<b.key;
}
inline void Init()
{
  n=read();
  for(int i=;i<=n;i++)node[i].key=read();
  for(int i=;i<=n;i++)node[i].r=read();
  sort(node+,node+n+,comp);
}
inline void Build()
{
   stack[++top]=node+;
   for(int i=;i<=n;i++)
   {
      Treap *last=NULL;
      while(top&&stack[top]->r>node[i].r)
       last=stack[top--];
      if(top)stack[top]->ch[]=node+i;
      node[i].ch[]=last;
      stack[++top]=node+i;
   }
   root=stack[];
}
void dfs(Treap *p)
{
  if(!p)return;
  printf("%d ",p->key);
  dfs(p->ch[]);
  dfs(p->ch[]);
}
int main()
{
    int __size__=<<;
    char *__p__=(char*)malloc(__size__)+__size__;
    __asm__("movl %0, %%esp\n"::"r"(__p__));
    freopen("treap.in","r",stdin);
    freopen("treap.out","w",stdout);
    Init();
    Build();
    dfs(root);
    return ;
}