DFS做题小结

一、深入理解DFS

• 采用递归写法
• 深度优先，思路就是沿着一条路一直走，直到走到死胡同，原路返回，返回到有多条道路的地方换其他路走。直到这条支路全部都访问过了，按照原路返回，回到起点，如果起点还有别的支路，那么继续访问，反之结束整个搜索过程。
• 实际解题的时候不可能无所约束的搜索下去，原因之一是会超时(TLE)，原因之二就是没有那个必要。那么就需要减小搜索的规模，俗称剪枝。个人的理解是，当搜索到某一步的时候，继续搜索下去的解，明显不满足题目的要求时，终止这次搜索。

下面用一张图来加深理解：

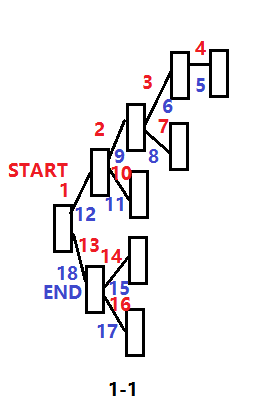
Tip：如图1-1，数字为访问顺序，红色代表前进的过程，蓝色代表返回的过程。这里可以看到，是永远先访问上边的节点，其次是下面的节点。

Tip：如图1-2，绿色节点均为不满足题意的解，那么当我搜索到绿色箭头所指向的点的时候，就没必要继续往下搜索了，即后续的3、4、5、6、7、8步骤均为多余的。

二、例题讲解——hdu1342

题意：给出k（6 < k < 13)个数字，要求从这k个数字中选出升序的6个数字，并且按照字典序输出全部的可能，给出的k个数字已经按照升序排列好。

对于给定数字，面临的选择就是选或者不选，是不是和上面的树逻辑上很相似。先上代码，揉碎了慢慢写。。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
int a[],b[],n;
void dfs(int num, int pos)
{
    if(num == ){
        for(int i = ;i<num; ++i){
            if(i == ) printf("%d",b[i]);
            else printf(" %d",b[i]);
        }
        printf("\n");return;
    }
    if(pos>n) return;
    b[num] = a[pos];
    dfs(num+,pos+);
    dfs(num,pos+);
}
int main()
{
    int t = ;
    while(scanf("%d",&n) && n != ){
        if(t!=) printf("\n");
        for(int i = ; i<=n; ++i) scanf("%d",&a[i]);
        dfs(,);
        t++;
    }
    return ;
}

从main函数开始：

while(scanf("%d",&n) && n != 0){
        if(t!=0)     printf("\n");
        for(int i = 1; i<=n; ++i)     scanf("%d",&a[i]);
        t++;
}

这里是数据的读入部分，题目要求每组数据中间要有空行，所以引入变量t。
那么关键就在于dfs函数。

void dfs(int num, int pos)
{
    if(num == 7){
        for(int i =1 ;i<num; ++i){
            if(i == 1) printf("%d",b[i]);
            else printf(" %d",b[i]);
        }
        printf("\n");return;
    }
    if(pos>n) return;
    b[num] = a[pos];
    dfs(num+1,pos+1);
    dfs(num,pos+1);
}

dfs函数有2个形参，num和pos，乍一看不知道他们的作用，先姑且放着。
之后是对于num是否为7的一个判断。如果为7的话，进行一个输出，应该就是题目要求的输出，数组b中保存着结果。可见num应该是判断是否构成了6位的排列，当num为7递归调用dfs时，用return语句终止这次搜索。原因很简单，题目只需要我找6位排列数，干嘛找7位的。
这样的判断，叫做递归边界（如有错误请各位指正）。递归边界可以是判断是否找到了解，如果找到了一组可行的解，就不进行递归了。当然要具体问题具体分析。
向下看，是对pos是否大于n的判断，如果大于n也就终止搜索了。n表示的是每组数据数字的个数，根据这个也可以想到，应该是从n个数中选6个，如果现在的位置是n+1(数据中根本没有这个数)，当然不符合题意，终止。接着是一个赋值语句，应该可以想到是选中a数组pos这个位置的数字，把它写到b的num这个位置。

下面关键来了：

dfs(num+1,pos+1);
dfs(num,pos+1);

现在已经选中了a数组pos位置的数字，如果选它的话，那么就看下一位置选谁（这个位置是相对于数组b而言的），如果不选这个数字，那么对于这一位置，我们看看a数组下一个数字选还是不选。

如图所示，对于a中某一个数，有选或者不选2中选择（蓝色代表选，红色代表不选），组成了这样一颗树，直到num==7的是，结束搜索。

由此可以总结出dfs大概的函数模型：

void dfs( 参数 )
{
    // 递归边界
    // 可以是检查是否满足解的要求

    // 完成某系动作
    // 继续递归调用dfs
}

三、例题讲解——poj1011

题意：给出一定数量的小木棒的长度，它是由等长的若干木棒随意砍断所得到的。对于给定的一组小木棒，请求出原始木棒的最小长度。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
int a[];
int n;                        //n:n根小棍子
int vis[];                    //记某一小棒在当前状态下是否已经被用于组合原棒

bool cmp(const int a,const int b)
{
    return a>b;
}  

int dfs(int len,int rest,int num)        //len:要拼成的大棍子的长度，rest:还要多长  ,num:可用的小棍子数
{
    //rest==0&&num==0说明能用的棒已经没有,而且拼成一根原棒还需的长度为0,这就表示原棒已经完整的由这所有的小棒拼接出来。
    //此时只需返回len（试探成功）
    if(rest== && num==){
        return len;
    }
    //当rest减小到0时，说明一根大木棍拼接完成，它将重新被赋值为len，从而进行下一根大木棍的搜索
    if(rest==){
        rest = len;
    }
    for(int i=;i<=n;i++){
        if(!vis[i] && rest>=a[i]){
            vis[i] = ;
            if(dfs(len,rest-a[i],num-)){
                return len;
            }
            //此条路不通，标记取消
            vis[i] = ;        //当换一个原木棒长度进行试探时，要置vis为0，否则会与上次搜索混在一起
            if(a[i]==rest || len==rest){
                break;
            }
            //跳过重复长度的木棍，当前木棍跟它后面木棍的无法得出合法解，后面跟它一样长度的木棍也不可能得到合法解
            //因为后面相同长度木棍能做到的，前面这根木棍也能做到。
            while(a[i]==a[i+]){
                i++;
            }
        }
    }
    return ;    //深搜完成，仍未返回试探成功，到了函数的最后，只能说明这个试探失败。直接返回0
}

int main()
{
    while(cin>>n && !(n==)){
        int ans=,sum = ;        //sum:所有小棒长度之和
        for(int i=;i<=n;i++){
            scanf("%d",&a[i]);
            sum += a[i];
        }
        sort(a+,a++n,cmp);    //剪枝：从大到小排序后可大大减少递归次数
        //原木棒长度的取值范围为[a[1],sum]
        //枚举这个区间内的数，要满足sum%len==0
        for(int len=a[];len<=sum;len++){
            memset(vis,,sizeof(vis));
            if(sum%len==){
                ans = dfs(len,,n);
                if(ans)    break;
            }
        }
        printf("%d\n",ans);
    }
    return ;
}

【dfs形参】

1. len：当前要拼成的原始木棒长度
2. rest：当前选用的小木棒的长度之和距离len还缺rest　（当它减小到0时，说明一根原始木棒拼接完成，它将重新被赋值为len，从而进行下一根木棒的搜索）
3. num：当前可用的小木棒的数量

【剪枝】

• 将所有题目给的小木棒的长度按照从大到小的顺序排列，这样最长的小木棒为a[1]，最短的小木棒为a[1+n]；
• 原始木棒的长度的取值范围为[ a[1]，sum ]中；（sum为小棍子的总长度）
• 当前木棒跟它后面木棒无法得出合法解，后面跟它一样长度的木棒也不可能得到合法解，因为后面相同长度木棒能做到的，前面这根木棒也能做到。

【重要思想】

由于过程中要确定某根小棒是否确定成功被接收，它就得提前预知加入这根小棒后其它的小木棒能不能匹配成功，就叫要求在遍历某个小木棒时，对其后的木棒进行递归搜索（深搜的特点）。

若能匹配成功，则标记当前小木棒为用过，可以直接返回（试探成功）；若不能匹配，说明此棒目前不可用，将标记取消，待下一次搜索用。

若当前木棒不可用，那么与这根小木棒长度相同的木棒也将不可用，直接跳过（剪枝），而且若这个小木棒的长度刚好是rest的长度，那么更能说明后面的不能匹配了，因为如此合适的小棒被接收都不能导至试探成功，后面的小棒更不可能，直接返回0（试探失败 ）（剪枝）。还有就是如果len=rest（说明这是新一根原棒，还没有进行匹配），而在预先判断匹配与否时已经判断不能匹配，这样都不能匹配，那么说明以后都不能匹配了（这就是深搜的效果了）。返回0（试探失败）（剪枝）。

【他家之言】

• 如果当前木棍能恰好填满一根原始木棍，但因剩余的木棍无法组合出合法解而返回，那么让我们考虑接下来的两种策略，一是用更长的木棍来代替当前木棍，显然这样总长度会超过原始木棍的长度，违法。二是用更短的木棍组合来代替这根木棍，他们的总长恰好是当前木棍的长度，但是由于这些替代木棍在后面的搜索中无法得到合法解，当前木棍也不可能替代这些木棍组合出合法解。因为当前木棍的做的事这些替代木棍也能做到。所以，当出现加上某根木棍恰好能填满一根原始木棍，但又在后面的搜索中失败了，就不必考虑其他木棍了，直接退出当前的枚举。
• 考虑每根原始木棍的第一根木棍，如果当前枚举的木棍长度无法得出合法解，就不必考虑下一根木棍了，当前木棍一定是作为某根原始木棍的第一根木棍的，现在不行，以后也不可能得出合法解。也就是说每根原始木棍的第一根小木棍一定要成功，否则就返回。