为什么我要放弃javaScript数据结构与算法（第三章）—— 栈

有两种结构类似于数组，但在添加和删除元素时更加可控，它们就是栈和队列。

第三章 栈

栈数据结构

栈是一种遵循后进先出（LIFO）原则的有序集合。新添加的或待删除的元素都保存在栈的同一端，称为栈顶，另一端就叫做栈底。在栈里， 新元素都靠近栈顶，旧元素都接近栈底。

栈也被用在编程语言的编译器和内存中保存变量、方法调用等。

创建栈

1. 先声明这个类

   function Stack(){
       // 各种属性和方法的声明
   }

1. 选择数组这种数据结构来保存栈里的元素

   let items = [];

1. 为栈声明一些方法

   • push（element（s））： 添加一个（或者几个）新元素到栈顶
   • pop（）：移除栈顶的元素，同时返回被移除的元素
   • peek（）：返回栈顶的元素，不会对栈做任何修改（这个方法不会移除栈顶的元素，仅仅返回它）
   • isEmpty（）：如果栈里没有任何元素的就返回true，否则就返回false.
   • clear（）：移除栈里的所有元素
   • size（）：返回栈里的元素个数，这个方法和数组的length属性很类似。

向栈添加元素

我们要实现的第一个方法是 push,这个方法负责向栈里添加新元素，该方法只添加元素到栈顶，也就是栈的末尾。

this.push = function(element){
    return items.push(element);
}

只能用 push 和 pop 方法添加和删除栈中元素，这样一来，我们的栈就自然遵从了 LIFO 原则。

向栈移除元素

我们要实现的第一个方法是 pop,这个方法主要用来移除栈里的元素。栈遵从 LIFO 原则，因此移出的是最后添加进去的元素。栈的 pop 方法可以这么写

this.pop = function(){
    return items.pop();
}

只能用 push 和 pop 方法添加和删除栈中元素，这样一来，我们的栈就自然遵从了 LIFO 原则。

查看栈顶元素

现在为类实现一些额外的辅助方法，如果想知道栈里最后添加的元素是什么，可以用 peek 方法，这个方法将返回栈顶的元素。

this.peek = function(){
    return items[items.length-1];
}

因为类内部是用数组保存元素的，所以访问数组的最后一个元素可以用 length - 1

检查栈是否为空

isEmpty ,如果栈为空的话就返回true，否则就返回false

this.isEmpty = function(){
    return items.length == 0;
}

类似于数组的 length 属性，我们也能实现栈的 length,对于集合，最好用 size 代替 length。因为栈的内部使用数组保存元素，所以能简单地返回栈的长度。

this.size = function(){
    return items.length;
}

清空和打印栈元素

实现 clear 方法。clear 方法用来移除栈里所有的元素，把栈清空。实现这个方法最简单的方式是

this.clear = function(){
    items = [];
    return null;
}

打印出来栈里面的内容，通过实现辅助方法 print 来实现。

this.print = function(){
    console.log(items.toString());
}

实例

function Stack(){
		let items = [];
		this.push = function(element){
			return items.push(element);
		}
		this.pop = function(){
			return items.pop();
		}
		this.peek = function(){
			return items[items.length-1];
		}
		this.isEmpty = function(){
			return items.length == 0;
		}
		this.size = function(){
			return items.length;
		}
		this.clear = function(){
			items = [];
		}
		this.print = function(){
			console.log(items.toString());
		}
	}
let stack = new Stack();
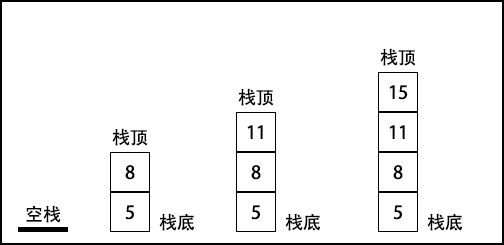
console.log(stack.isEmpty()); // true 判断是否为空
stack.push(5); // 往栈里添加元素 5
stack.push(8); // 往栈里添加元素 8
console.log(stack.peek()); // 查看最后一个元素 8
stack.push(11); // 往栈里添加元素 11
console.log(stack.size()); // 3 输出栈的元素个数
console.log(stack.isEmpty()); // false 判断是否为空
stack.push(15); // 往栈里添加元素 15
stack.print(); // 5,8,11,15 输出栈里的元素

下面是流程图

ECMAScript6 和 Stack 类

创建了一个可以当做类来使用的 Stack 函数。JavaScript 函数都有构造函数，可以用来模拟类的行为。我们声明一个私有的 items变量，它只能被 Stack 函数/类访问。然而，这个方法为每个类的实例都创建了一个 items 变量的副本。因此如果要创建多个 Stack实例，就不太适合。我们可以尝试用 ES6语法来声明 Stack 类。

用 ES6 声明 Stack 类

class Stack{
    constructor(){
        this.items = []; // {1}
    }
    push(elememt){
        this.items.push(element);
    }
    // 其他方法
}

只是用 ES6 的简化语法把 Stack 函数转换成 Stack 类。这种方法不能像其他语言（Java、C++、C#）一样直接在类里面声明变量，只能在类的构造函数 constructor 里声明，在类的其他函数里用 this.nameofVariable 就可以引用这个变量。

尽管代码看起来更加简洁、更漂亮，变量 items 却是公共的。ES6 类是基于原型的。虽然基于原型的类比基于函数的类更节省内存，也更适合创建多个实例，却不能够声明私有属性（变量）或方法。而且，在这种情况下，我们希望 Stack 类的用户只能访问暴露给类的方法。否则，就有可能从栈的中间移除元素（因为我们用数组来存储其值），这不是我们希望看到的。

用ES6的限定作用域 Symbol 实现类

ES6 新增了一种叫做 Symbol 的基本类型，它是不可变的，可以用作对象的属性。

let _items = Symbol(); // 声明了 Symbol 类型的变量
class Stack{
    constructor(){
        this[_items] = [] // 要访问 _items,只需把所有的 this.items都换成 this.[_items]
    }
    push(element){
        return this[_items].push(element);
    }
    pop (){
        return this[_items].pop();
    }
    peek (){
        return this[_items][this[_items].length-1];
    }
    isEmpty (){
        return this[_items].length == 0;
    }
    size (){
        return this[_items].length;
    }
    clear (){
        this[_items] = [];
    }
    print (){
        console.log(this[_items].toString());
    }
}

这种方法创建了一个假的私有属性，因为ES6 新增的Object.getOwnPropertySymbols 方法能够取到类里面声明的所有 Symbols 属性。下面是一个破坏 Stack 类的例子

let stack = new Stack();
stack.push(5);
stack.push(8);
let objectSymbols = Object.getOwnPropertySymbols(stack);
console.log(objectSymbols.length); // 1
console.log(objectSymbols); // [Symbol()]
console.log(objectSymbols[0]); // Symbol()
stack[objectSymbols[0]].push(1);
stack.print(); // 5,8,1

很明显可以通过访问 stack[objectSymbol[0]] 得到 _items。并且 _items属性是一个数组，可以进行任意的数组操作，比如从中间删除或者是添加元素。我们操作的是栈，不应该有这种行为出现。

用ES6类的 WeakMap 实现类

有一种数据类型可确保属性是私有的，这就是 WeakMap。后面会深入探讨 Map 这种数据结构，现在只需要知道 WeakMap 可以存储键值对，其中键是对象，值可以是任意数据类型。

如果使用 WeakMap 来存储 items 变量，那么 Stack 类是这样的

const items = new WeakMap(); // 声明了一个 WeakMap 类型的变量 items
class Stack{
    constructor(){
        items.set(this, []) // 在 constructor 中，以this（Stack类自己引用）为键，把代表栈的数组存入 items
    }
    push(element){
        let s = items.get(this);
        s.push(element);
    }
    pop (){
        let s = items.get(this);
        let r = s.pop();
        return r;
    }
    peek (){
        let s = items.get(this);
        return s[s.length-1];
    }
    isEmpty (){
        let s = items.get(this);
        return s.length == 0;
    }
    size (){
        let s = items.get(this);
        let r = s.length
        return r;
    }
    clear (){
        items.set(this, [])
    }
    print (){
        let s = items.get(this);
        console.log(s.toString());
    }
}

现在 items 在 Stack 类里是真正的私有属性了，但是还有一件事要做， items 现在仍然是在 Stack 类以外声明的，因此任何谁都可以改动它。我们可以用一个闭包（外层函数）把 Stack 类包起来，这样就可以在这个函数里访问 WeakMap

let stack = (function(){
    const items = new WeakMap();
    class Stack {
        constructor(){
            items.set(this, []);
        }
        // 其他方法
    }
    return Stack; // 当 Stack 函数里的构造函数被调用时，会返回 Stack 类的一个实例。
})()

现在，Stack 类有一个名为 items 的私有属性。然后用这种方法的话，扩展类无法继承其属性。将其与最开始用 function 实现的 Stack 类来做个比较，我们会发现一些相似之处。

事实上，尽管 ES6 引入了类的语法，我们仍然不能像在其他编程语言中一样声明私有属性或方法。有很多种方法都可以达到相同的效果，但无论是语法还是性能，这些方法都有各自的缺点和优点。

用栈解决问题

栈的实际应用非常广泛。在回溯问题中，它可以存储访问过的任务或是路径、撤销的操作。Java 和 C# 用栈来存储变量和方法调用，特别是处理递归算法时，有可能抛出一个栈溢出异常（stack overflow）

下面，学习使用栈的三个最著名的算法实例。首先是十进制转二进制的问题，以及任意进制转换的算法，然后是平衡圆括号问题，最后，会学习栈解决汉诺塔的问题。

从十进制到二进制

计算科学中，二进制非常重要，因为计算机里的所有内容都是用二进制数字表示（0和1）。没有十进制和二进制相互转化的能力，与计算机交流就很困难。要把十进制化成十进制，将该十进制数字和2整除，直到结果为0为止。

实例:数字10转为二进制的数字。

function divideBy2(decNumber){
    var remStack = new Stack(),
    rem,
    binaryString = '';
    while(decNumber > 0){
        rem = Math.floor(decNumber % 2); // 拿到被2整除的余数
        remStack.push(rem);
        decNumber = Math.floor(decNumber / 2) // 拿到被2整除的整数
    }
    while (! remStack.isEmpty()){
        binaryString += remStack.pop().toString();
    }
    return binaryString;
}

console.log(divideBy2(10)); // 1010
console.log(divideBy2(233)); // 11101001
console.log(divideBy2(100)); // 11101001

JavaScript有数字类型，但是不会区分究竟是整数还是浮点数，使用 Math.floor 让除法只返回整数部分。

进制转换算法

可以传入任意进制的基数作为参数

function baseConverter(decNumber, base){
    var remStack = new Stack(),
    rem,
    baseString = '',
    digits = '0123456789ABCDEF';
    while(decNumber > 0){
        rem = Math.floor(decNumber % base); // 拿到被base整除的余数
        remStack.push(rem);
        decNumber = Math.floor(decNumber / base) // 拿到被base整除的整数
    }
    while (! remStack.isEmpty()){
        baseString += digits[remStack.pop()];
    }
    return baseString;
}
console.log(baseConverter(100345,2)); // 11000011111111001
console.log(baseConverter(100345, 8)); // 303771
console.log(baseConverter(100345, 16)); // 187F9

需要改动的地方：在将十进制转为二进制的时候，余数是0或者1，转为八进制的时候，余数为0_{7，同理16进制是0}9加上A~F。所以要做个转换，通过定义 digits ，digits[remStack.pop()] 来实现转化。

小结

通过这一章，学习了栈这一数据结构的相关内容。可以用代码自己实现栈，还讲解了栈里面的相关方法。

书籍链接： 学习JavaScript数据结构与算法