（数据科学学习手札17）线性判别分析的原理简介&Python与R实现

之前数篇博客我们比较了几种具有代表性的聚类算法，但现实工作中，最多的问题是分类与定性预测，即通过基于已标注类型的数据的各显著特征值，通过大量样本训练出的模型，来对新出现的样本进行分类，这也是机器学习中最多的问题，而本文便要介绍分类算法中比较古老的线性判别分析：

线性判别

最早提出合理的判别分析法者是R.A.Fisher（1936），Fisher提出将线性判别函数用于花卉分类上，将花卉的各种特征利用线性组合方法变成单变量值，即将高维数据利用线性判别函数进行线性变化投影到一条直线上，再利用单值比较方法来对新样本进行分类，主要步骤如下：

　　Step1：求线性判别函数；

　　Step2：计算判别界值；

　　Step3：建立判别标准（这里与模糊分类中的隶属度有些相似，即离哪一类的投影中心最近，就将样本判别为哪一类）

下面分别利用Python，R，基于著名的花卉分类数据集iris进行演示：

Python

我们利用sklearn包中封装的LinearDiscriminantAnalysis对iris构建线性判别模型，因为LDA实际上是将高维数据尽可能分开的投影到一条直线上，因此LDA也可以对特定数据进行降维转换：

'''Fisher线性判别分析'''
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from matplotlib.pyplot import style
from sklearn.model_selection import train_test_split

style.use('ggplot')

iris = datasets.load_iris()

X = iris.data
y = iris.target

'''展示LDA的降维功能'''
target_names = iris.target_names

'''设置压缩到1维'''
lda = LinearDiscriminantAnalysis(n_components=1)

'''利用线性判别函数将四维的样本数据压缩到一条直线上'''
X_r2 = lda.fit(X,y).transform(X)
X_Zero = np.zeros(X_r2.shape)
'''绘制降维效果图'''
for c,i,target_names in zip('ryb',[0,1,2],target_names):
    plt.scatter(X_r2[y == i],X_Zero[y == i],c=c,label=target_names,s=5)

plt.legend()
plt.grid()

降维后的效果图如下：

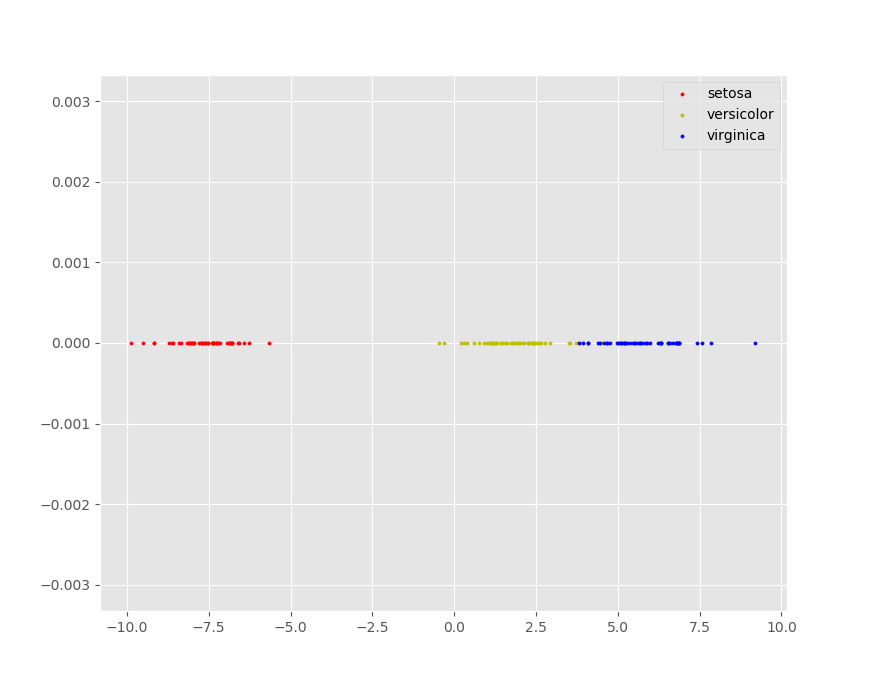
下面正式对iris数据集进行LDA分类，这里用到一个新的方法，是sklearn.model_selection.train_test_split，它的作用是根据设置的训练集与测试集的比例进行随机分割，我们利用从样本集中分割的7成数据作为训练集，3成数据进行测试，过程及结果如下：

'''利用sklearn自带的样本集划分方法进行分类，这里选择训练集测试集73开'''
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3)
'''搭建LDA模型'''
lda = LinearDiscriminantAnalysis(n_components=1)
'''利用分割好的训练集进行模型训练并对测试集进行预测'''
ld = lda.fit(X_train,y_train).predict(X_test)
'''比较预测结果与真实分类结果'''
print(np.array([ld,y_test]))
'''打印正确率'''
print('正确率：',str(lda.score(X_test,y_test)))

结果如下：

可以看出，在iris上取得了非常高的准确率。

R

在R中做LDA需要用到MASS包中的lda(formula~feature1+feature2+...+featuren,data=df)，其中formula表示数据集中表示分类标注的列，右边的各种feature表示将要使用到的分类特征值，也即是构建线性判别函数要用到的基础变量，data指保存全部数据的数据框，具体过程如下：

> #Fisher线性判别
> rm(list=ls())
> library(MASS)
> data(iris)
> data <- iris
> data$Species = as.character(data$Species)
> #创造类别变量
> data$type[data$Species == 'setosa'] = 1
> data$type[data$Species == 'versicolor'] = 2
> data$type[data$Species == 'virginica'] = 3
> #利用简单随机抽样将样本集划分为训练集与验证集
> sam <- sample(1:length(data[,1]),105)
> train <- data[sam,]
> test <- data[-sam,]
> #根据样本数据创建线性判别分析模型
> ld <- lda(type~Sepal.Length+Sepal.Width+Petal.Length+Petal.Width,data=train)
> #将样本集作为验证集求分类结果
> Z <- predict(ld)
> #保存预测类别
> newType <- Z$class
> #与真实分类结果进行比较
> cbind(train$type,Z$x,newType)
             LD1         LD2 newType
74  2 -2.0419740 -1.16551052       2
93  2 -1.2286978 -1.34868982       2
124 3 -4.2056288 -0.39378496       3
43  1  7.0499296 -0.38479505       1
141 3 -6.3297144  1.43240686       3
112 3 -5.2009805 -0.39665336       3
75  2 -1.2076317 -0.53028083       2
83  2 -0.8607055 -1.04255122       2
128 3 -3.7958024  0.38283281       3
134 3 -3.5521695 -0.79338125       2
84  2 -4.1930475 -0.86304028       3
80  2  0.2455854 -1.48598565       2
16  1  8.9754828  2.99336222       1
35  1  6.7862663 -0.74053169       1
64  2 -2.4399568 -0.53150309       2
79  2 -2.4024680 -0.24830622       2
142 3 -4.9647448  1.48158101       3
54  2 -2.2217845 -1.93554530       2
14  1  7.3092968 -0.99420385       1
119 3 -8.8253015 -0.67042900       3
71  2 -3.3701925  0.94839271       3
44  1  6.2098650  0.99672773       1
29  1  7.6841973  0.08156876       1
62  2 -1.7099434  0.15332464       2
59  2 -1.6648086 -0.67372500       2
77  2 -2.3932456 -0.84052244       2
27  1  6.6078477  0.36272030       1
101 3 -7.2690741  1.94879260       3
91  2 -2.1739793 -1.53761667       2
40  1  7.4330661  0.03443993       1
103 3 -5.9833783  0.46642759       3
121 3 -5.9399677  1.45493705       3
51  2 -1.3784535  0.24058778       2
88  2 -2.5153892 -2.12899905       2
6   1  7.5334551  1.60652494       1
148 3 -4.7085798  0.61397476       3
76  2 -1.3919721 -0.13234144       2
10  1  7.0733099 -0.92823629       1
7   1  7.0416936  0.27174257       1
104 3 -5.1966351 -0.20937105       3
24  1  6.0120553  0.24387476       1
137 3 -6.0383747  2.20984770       3
61  2 -1.2257443 -3.03469429       2
41  1  7.6466593  0.57623503       1
26  1  6.4775174 -1.04708182       1
70  2 -1.0443574 -1.74662921       2
31  1  6.5351351 -0.78766052       1
85  2 -2.5818237  0.01276122       2
36  1  7.5972776 -0.33972390       1
4   1  6.6085362 -0.73929708       1
130 3 -4.2970292 -0.42496657       3
95  2 -1.8418994 -0.99664464       2
111 3 -4.1644831  1.17871159       3
117 3 -4.7101562  0.09594447       3
48  1  6.9765285 -0.43315849       1
106 3 -7.0303766  0.13158736       3
69  2 -3.5167119 -2.05931691       2
131 3 -5.9675456 -0.52249341       3
92  2 -2.0719645 -0.22536449       2
22  1  7.3872921  1.18564382       1
39  1  6.6977209 -0.90199151       1
125 3 -5.3082628  1.33894916       3
47  1  7.9455957  1.02129249       1
108 3 -5.9474167 -0.54626897       3
123 3 -7.2281863 -0.62126561       3
25  1  6.4877846 -0.15448692       1
96  2 -0.9672993 -0.40896608       2
149 3 -5.4267988  2.11763536       3
58  2 -0.1967945 -1.90480909       2
100 2 -1.4146638 -0.69091758       2
107 3 -4.3326495 -0.90276305       3
89  2 -1.1216984 -0.17330958       2
67  2 -2.4633370  0.01193815       2
45  1  6.7958450  1.25408059       1
138 3 -4.5932952  0.35495424       3
30  1  6.6519961 -0.52865075       1
17  1  8.3010066  1.79668640       1
9   1  6.3297286 -1.20813011       1
135 3 -4.6952607 -1.73516107       3
18  1  7.5140148  0.52828312       1
145 3 -6.4564371  2.08976755       3
68  2 -0.6703941 -1.51304115       2
12  1  7.0634482 -0.01186583       1
23  1  8.4484974  0.79139590       1
20  1  7.8504400  1.25653745       1
15  1  9.4800594  1.72576966       1
147 3 -5.0367690 -0.77081719       3
46  1  6.4557628 -0.76347342       1
60  2 -1.7902528 -0.66467281       2
19  1  7.8221244  1.15898751       1
144 3 -6.3829867  1.36026786       3
1   1  7.8010583  0.34057853       1
90  2 -1.8695758 -1.41834884       2
53  2 -2.2846205  0.07502495       2
115 3 -6.4317784  0.89801781       3
146 3 -5.4512238  1.17626549       3
78  2 -3.3451866  0.14511863       2
99  2  0.3864166 -1.31670824       2
118 3 -6.0412297  2.34012590       3
38  1  8.1457196  0.41229523       1
139 3 -3.6631579  0.43078471       3
105 3 -6.4339941  0.70414177       3
132 3 -4.7729922  2.10651473       3
110 3 -6.3994587  2.67334311       3
72  2 -0.9858025 -0.64502336       2
> #打印混淆矩阵
> (tab <- table(newType,train$type))

newType  1  2  3
      1 35  0  0
      2  0 33  1
      3  0  2 34
> #显示正确率
> cat('Accuracy:',sum(diag(tab))/length(train[,1]))
Accuracy: 0.9714286
> #将验证集代入训练好的模型中计算近似泛化误差
> T <-predict(ld,test)
> #与真实分类结果进行比较
> cbind(test$type,T$x,T$class)
             LD1         LD2
2   1  6.8020498 -0.95158956 1
3   1  7.2276597 -0.38602966 1
5   1  7.9179194  0.59958829 1
8   1  7.3738228  0.03485147 1
11  1  8.1391093  0.80900002 1
13  1  7.0298500 -1.13888262 1
21  1  7.2270204 -0.06187541 1
28  1  7.6684138  0.29262662 1
32  1  7.0367090  0.40861452 1
33  1  9.0120836  1.65651141 1
34  1  9.2707624  2.14912000 1
37  1  8.2299196  0.38647275 1
42  1  5.2371900 -2.52488607 1
49  1  8.0798659  0.80941155 1
50  1  7.3896062 -0.17620640 1
52  2 -1.6371815  0.52584233 2
55  2 -2.4742435 -0.55650250 2
56  2 -2.1822152 -0.88107904 2
57  2 -2.1911397  0.87747596 2
63  2 -1.2405414 -2.75931501 2
65  2 -0.3383635 -0.19420599 2
66  2 -1.1566243  0.12584525 2
73  2 -3.6967069 -1.47409522 2
81  2 -1.0878173 -1.95727554 2
82  2 -0.6088858 -2.09743977 2
86  2 -1.8089897  1.23238953 2
87  2 -2.0193315  0.17092876 2
94  2 -0.3136555 -2.16381886 2
97  2 -1.4304473 -0.47985972 2
98  2 -1.3261184 -0.52945776 2
102 3 -5.1726649 -0.29910341 3
109 3 -6.0478550 -1.34049085 3
113 3 -5.3935569  0.65782366 3
114 3 -5.6792727 -0.58064337 3
116 3 -5.4686329  1.64715619 3
120 3 -4.5946379 -2.29619567 3
122 3 -5.0183151  0.24310322 3
126 3 -4.9026833  0.37255836 3
127 3 -3.8968800 -0.08723483 3
129 3 -6.1746269  0.09473298 3
133 3 -6.4616705  0.28243757 3
136 3 -6.5857811  0.74428684 3
140 3 -4.9663213  0.96355072 3
143 3 -5.1726649 -0.29910341 3
150 3 -4.2980648  0.28857515 3
> #打印混淆矩阵
> (tab <- table(T$class,test$type))

     1  2  3
  1 15  0  0
  2  0 15  0
  3  0  0 15
> #显示正确率
> cat('Accuracy:',sum(diag(tab))/length(test[,1]))
Accuracy: 1
> #Fisher线性判别
> rm(list=ls())
> library(MASS)
> data(iris)
> data <- iris
> data$Species = as.character(data$Species)
> #创造类别变量
> data$type[data$Species == 'setosa'] = 1
> data$type[data$Species == 'versicolor'] = 2
> data$type[data$Species == 'virginica'] = 3
> #利用简单随机抽样将样本集划分为训练集与验证集
> sam <- sample(1:length(data[,1]),105)
> train <- data[sam,]
> test <- data[-sam,]
> #根据样本数据创建线性判别分析模型
> ld <- lda(type~Sepal.Length+Sepal.Width+Petal.Length+Petal.Width,data=train)
> #将样本集作为验证集求分类结果
> Z <- predict(ld)
> #保存预测类别
> newType <- Z$class
> #与真实分类结果进行比较
> cbind(train$type,Z$x,newType)
             LD1          LD2 newType
44  1  6.5356943  1.380095755       1
150 3 -5.0777607  0.353229454       3
48  1  7.2092979 -0.233679182       1
17  1  8.7810490  1.832128789       1
11  1  8.5106371  0.591364581       1
13  1  7.4261015 -0.949875862       1
82  2 -0.7168056 -1.805629506       2
19  1  8.2170070  0.870266056       1
123 3 -7.9020752 -1.233817765       3
23  1  8.7554448  0.980676590       1
59  2 -1.8788410 -0.915972039       2
70  2 -1.2367635 -1.516788339       2
146 3 -5.6852127  1.788579457       3
142 3 -5.0723482  2.082228707       3
115 3 -6.9597642  1.869494439       3
7   1  7.2188221  0.472577805       1
112 3 -5.6667730 -0.156736416       3
117 3 -5.4232144 -0.112017744       3
26  1  6.8888800 -0.860736454       1
111 3 -4.6405840  1.346460523       3
29  1  8.1491362  0.125965565       1
81  2 -1.2242456 -1.597693375       2
14  1  7.6286098 -0.598455540       1
110 3 -7.1444731  2.585994755       3
40  1  7.7798631  0.022078382       1
39  1  6.9782244 -0.504346286       1
68  2 -1.0104685 -1.671771426       2
20  1  8.0502422  1.117799195       1
31  1  6.7929797 -0.656064848       1
134 3 -4.1319678 -1.006493240       2
73  2 -4.0110318 -1.372974920       2
4   1  6.8227612 -0.537268125       1
108 3 -6.6972047 -1.217364668       3
54  2 -2.3695531 -1.376553027       2
148 3 -5.1575482  0.848139667       3
141 3 -6.8305530  1.864676411       3
109 3 -6.6173517 -1.422188092       3
50  1  7.7923809 -0.058826655       1
91  2 -2.7513769 -1.544578568       2
97  2 -1.8728790 -0.435815301       2
96  2 -1.4911207 -0.557876549       2
77  2 -2.5464899 -1.021564544       2
66  2 -1.2439344  0.003029162       2
145 3 -7.0771380  2.462076368       3
38  1  8.3218303  0.213545770       1
45  1  6.7744745  0.999164236       1
58  2 -0.3713519 -1.340382308       2
35  1  7.1622529 -0.552177665       1
36  1  8.1741719 -0.035844508       1
57  2 -2.7067243  0.719387605       2
27  1  6.9079284  0.551777520       1
132 3 -5.6031449  1.030132762       3
128 3 -4.3392145  0.561003821       3
87  2 -2.2635929 -0.006748767       2
88  2 -2.4886790 -1.851739918       2
118 3 -7.1004619  1.347087687       3
119 3 -9.4291409 -0.890616169       3
46  1  6.9234400 -0.316289540       1
33  1  9.0573501  1.063438766       1
10  1  7.4135836 -0.868970825       1
78  2 -3.6650096  0.105534552       2
32  1  7.6166932  0.640755164       1
139 3 -4.1962691  0.674830697       3
103 3 -6.5226603  0.373114540       3
43  1  7.2390794 -0.114882460       1
121 3 -6.4785762  1.623818440       3
15  1 10.1229028  1.482252025       1
125 3 -6.0718150  1.194903725       3
92  2 -2.5655637 -0.379597733       2
21  1  7.6071362 -0.210545218       1
116 3 -6.0199587  2.084095792       3
95  2 -2.2468978 -0.820309281       2
93  2 -1.3874483 -1.124059988       2
135 3 -5.6483660 -2.247095684       3
52  2 -1.9604386  0.420606745       2
37  1  8.8751646  0.414644969       1
127 3 -4.2307963  0.275427178       3
137 3 -6.8919261  2.468751536       3
98  2 -1.5631688 -0.569521563       2
72  2 -1.0384324 -0.432712540       2
80  2  0.2825956 -1.208391313       2
67  2 -3.1266046  0.070901690       2
120 3 -4.9979151 -2.051118149       3
114 3 -6.2027782  0.131952933       3
69  2 -3.4910411 -1.516772693       2
130 3 -4.8967334 -1.106964081       3
42  1  5.9270652 -1.555646363       1
64  2 -2.9521004 -0.683186676       2
86  2 -2.4035699  1.146743118       2
75  2 -1.3368410 -0.579461256       2
143 3 -5.8335378  0.090796722       3
140 3 -5.3380144  1.122071295       3
1   1  8.1663998  0.325667325       1
83  2 -1.0009115 -0.820471045       2
28  1  8.0234544  0.211840448       1
85  2 -3.3529324  0.080841383       2
89  2 -1.5995061 -0.127256512       2
18  1  7.9150690  0.642460485       1
147 3 -5.2724641 -0.214659306       3
105 3 -7.1968652  0.828583809       3
41  1  8.0580144  0.756287362       1
63  2 -1.1801689 -2.546513654       2
122 3 -5.6685504  0.829975549       3
107 3 -5.0735507 -0.234382628       3
47  1  8.0454637  0.692149004       1
> #打印混淆矩阵
> (tab <- table(newType,train$type))

newType  1  2  3
      1 36  0  0
      2  0 33  1
      3  0  0 35
> #显示正确率
> cat('Accuracy:',sum(diag(tab))/length(train[,1]))
Accuracy: 0.9904762> #将验证集代入训练好的模型中计算近似泛化误差
> T <-predict(ld,test)
> #与真实分类结果进行比较
> cbind(test$type,T$x,T$class)
             LD1         LD2
2   1  7.2879346 -0.63805255 1
3   1  7.5785711 -0.12979200 1
5   1  8.1836634  0.52536908 1
6   1  7.7566121  1.39670067 1
8   1  7.6666992  0.02704823 1
9   1  6.5916877 -0.80793523 1
12  1  7.1842622 -0.07186911 1
16  1  9.2604596  2.57316476 1
22  1  7.6684840  1.23986044 1
24  1  6.3832248  0.56001189 1
25  1  6.4159345 -0.39844020 1
30  1  6.8102433 -0.45636309 1
34  1  9.5320477  1.66891133 1
49  1  8.3974733  0.59633443 1
51  2 -1.5423430 -0.14371955 2
53  2 -2.5494836 -0.23440252 2
55  2 -2.6250939 -0.47214778 2
56  2 -2.7716342 -0.95711830 2
60  2 -2.1825564 -0.15706564 2
61  2 -1.2921165 -2.34199387 2
62  2 -2.0187853  0.38256324 2
65  2 -0.4493874  0.22229672 2
71  2 -4.0485780  1.06926437 3
74  2 -2.5798663 -1.51150491 2
76  2 -1.4875258 -0.18673290 2
79  2 -2.8043766 -0.14370961 2
84  2 -4.8532177 -0.86952245 3
90  2 -2.1086982 -0.98708920 2
94  2 -0.3886155 -1.54008407 2
99  2  0.5024002 -0.51222584 2
100 2 -1.7471972 -0.52169018 2
101 3 -8.2981213  2.15538466 3
102 3 -5.8335378  0.09079672 3
104 3 -6.0360789 -0.40566699 3
106 3 -7.7496056 -0.41373390 3
113 3 -5.8377150  0.82345220 3
124 3 -4.5041691 -0.03313161 3
126 3 -5.6507584 -0.30162799 3
129 3 -6.8073348  0.34501073 3
131 3 -6.4535806 -0.88255921 3
133 3 -7.0586655  0.66180389 3
136 3 -6.8585571  0.75916772 3
138 3 -5.4059508  0.08768402 3
144 3 -7.1039586  1.41107423 3
149 3 -6.2415407  2.37464228 3
> #打印混淆矩阵
> (tab <- table(T$class,test$type))

     1  2  3
  1 14  0  0
  2  0 15  0
  3  0  2 14
> #显示正确率
> cat('Accuracy:',sum(diag(tab))/length(test[,1]))
Accuracy: 0.9555556

可以看出，和Python中的效果相差无几。

以上就是关于线性判别的基本内容，如有意见望提出。